产业共性技术产学研协同研发策略的微分博弈研究

马永红，刘海礁，柳 清

(1.哈尔滨工程大学经济管理学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学企业创新研究所，黑龙江 哈尔滨 150001；3.美国北卡罗莱纳大学教堂山分校中国城市研究中心，北卡罗莱纳州 教堂山 27599；4.哈尔滨工业大学建筑学院，黑龙江 哈尔滨 150001)

1 引言

产业共性技术作为很多领域内已经或未来可能被广泛应用，其研发成果可以共享并对整个产业或多个产业及其企业产生深度影响的一类竞争前阶段的技术[1-2]，对一个国家的产业发展和科技进步具有重要意义。许多发达国家十分重视产业共性技术的研发活动，如欧盟的科技框架计划、美国的技术创新计划(TIP)和先进技术计划都包含了对产业共性技术研发的支持。我国政府也高度重视产业共性技术的研发活动，习近平总书记强调：“要围绕产业链部署创新链，要聚集产业发展需求，集成各类创新资源，着力突破共性关键技术，加快科技成果转化和专业化，培育产学研结合、上中下游衔接、大中小企业协同的良好创新格局”。基于产业共性技术潜在的市场价值，我国政府在产业共性技术的研发供给中扮演了重要角色，但产业共性技术种类繁多，研发成本高，政府不可能完全主导产业共性技术的研发供给。产学研合作作为协同创新的一种组织形式，大学、科研院所与企业的互补性资源投入，既分担了研发的风险，又保证了研发资金的有效供给，可有效补充产业共性技术的研发供给的不足。因此，如何统筹运用创新资源，深入剖析产学研合作为基础的产业共性技术协同研发机制意义重大。

现有产业共性技术研究大多集中在概念理论、识别测度以及研发供给等方面，例如Tassey[3-6]最早提出共性技术的概念并进行了系统的研究，他先后提出“技术开发模型”和“基于技术的经济增长模型”，并将技术分为基础技术、共性技术和专有技术，分析了共性技术的构成，侧重对共性技术政策的研究；在Tassey研究的基础上，李纪珍[1]对产业共性技术的概念、分类和制度供给进行了介绍；马明杰[2]探讨了共性技术的概念和内涵，并指出共性技术受一个国家经济和技术发展水平的影响；许瑞阳和徐峰[7]基于科技计划管理的视角，对产业共性技术的界定及选择方法进行了研究；樊霞和吴进[8]通过系统化梳理我国的共性技术政策创新文本，对我国的共性技术创新政策进行了研究；栾春娟[9]通过对产业共性技术的界定，提出战略性新兴产业共性技术的测度指标；骆正清和戴瑞[10]综合运用问卷调查法、主成分分析法和改进的德尔菲方法对共性技术的选择方法进行了研究；黄鲁成和张静[11]通过构建综合文本挖掘、德温特手工代码共现、专利引用确立的共性技术识别方法框架，提出了基于专利分析的产业共性技术识别方法；刘波等[12]通过对扎根理论、文献分析法和TOPSIS评价模型的实例应用，提出了在共性技术筛选中更重要的指标；周潇等[13]通过构建政府与企业对产业共性技术研发投资的博弈模型，研究了中央和地方两种类型政府资助龙头企业或一般企业时的最优投资策略组合；刘洪民等[14]通过构建制造业共性技术研发知识管理流程绩效评价的指标体系，提出了AHP和FCE模型相结合的多层次模糊综合评价模型可以较好地对制造业共性技术协同研发的知识管理流程绩效进行综合评价；郑月龙等[15]基于政府视角，对以企业研发投入最大化为目标的共性技术市场化过程最优研发支持合同的影响因素进行了研究。

在经济全球化环境下，创新越来越具有开放性，科技知识的创造、创新和应用部门之间需要构建开放式的协同创新[16]。随着产学研协同创新理论的兴起，产业共性技术产学研协同创新相关问题的研究开始受到学者们的广泛关注，例如薛捷和张振刚[17]通过归纳国外产业共性技术开发方面的基本情况和发展经验，提出我国在共性技术开发上应采用“官产学研”合作的组织形式；周国林[18]在分析和评价国内外共性技术产学研联盟组织的基础上，提出了优化我国产业共性技术的产学研组织模式的总体思路，樊霞等[19-20]运用倾向得分匹配方法基于USPTO的中国专利数据，对中国产业共性技术创新的产学研合作影响进行了研究，随后在运用平均技术共现率(MTCR) 和平均技术共类指数(MTCI) 对生物技术领域专利技术进行共性特征的分析基础上，引入倾向得分匹配方法，对产学研合作对共性技术创新的影响效用进行了研究；殷辉和陈劲[21]对不同情景下分别来自新兴产业和成熟产业的两类异质企业间与学研机构合作研发共性技术的演化博弈过程和稳定策略进行了分析。尽管现有研究对产业共性技术产学研协同创新的组织模式、产学研合作对产业共性技术创新的影响等方面进行了分析和探讨，但很少有文献基于微观层面对产业共性技术产学研协同创新中大学、科研院所与企业的决策等相关问题进行研究。此外，产业共性技术作为连接大学、科研院所基础技术与企业专有技术的“桥梁”[22]，在其产学研协同研发过程中，大学、科研院所与企业基于异质性的创新资源开展合作，大学、科研院所希望通过与企业的合作扩充科研经费、促进科研成果转化以及从企业的现实需求中提炼出科学问题[23]，企业则希望通过与大学、科研院所的合作分散创新风险和弥补自身基础研究能力的不足[24]，但这种异质性又将导致大学、科研院所与企业的合作动因和行为目标存在冲突[25-26]。因此，针对上述冲突基于微观视角对产业共性技术产学研协同研发过程中大学、科研院所与企业的决策等相关问题进行研究具有重要意义。

事实上，由于产业共性技术具有长期性、动态性、复杂性等特征，需要不断的更新和修正。产业共性技术研发的速率和频率又随着科技和信息迅猛发展而提高，这意味着应考虑基于决策主体的动态行为对同一个时空区域内的产业共性技术协同研发问题进行研究。微分博弈作为处理双决策主体在同一个时空区域内竞争和合作的重要模型，已有学者将其引入产学研协同创新等问题的研究。例如于娱和施琴芬[27]通过构建微分博弈模型，运用哈密尔顿-雅可比-贝尔曼方程分别求得了Nash非合作博弈、Stackelberg主从博弈和协同合作博弈情形下大学和企业的最优知识共享策略；朱怀念等[28]在于娱等人研究的基础上，在考虑随机因素干预的情况下，通过构建随机微分博弈模型，进一步阐释了Stackelberg主从博弈和协同合作博弈情形下不同协同创新主体均衡的知识共享策略，但上述研究没有考虑协同创新主体间的协调问题。而现实中协同创新决策主体的决策过程往往受到其自身收益的影响，也就是说当协同创新行为主体的收益均达到最优时，可实现协同创新主体间的协调。因此，本文在上述研究的基础上，引入微分博弈的方法基于动态视角对产业共性技术产学研协同研发问题进行研究，运用哈密尔顿-雅可比-贝尔曼方程(简称HJB方程)分别考察三种研发博弈情形下大学、科研院所与企业各自的最优研发努力程度、最优研发收益和双方最优研发总收益，探讨研发补贴对产业共性技术产学研协同研发的作用机制，寻求动态框架下产业共性技术产学研协同创新主体间的协调机制。期望所得到的相关结论能为产业共性技术产学研协同研发激励机制、收益分配和契约设计等方面的科学决策提供支持，为推动产业共性技术产学研协同研发提供正确的理论依据。

2 问题描述与基本假设

2.1 问题描述

为简化研究，本文仅考察完全理性且拥有完全信息的单个研究机构(大学、科研院所)S和单个企业E参与的产业共性技术协同研发，研究机构主要负责产业共性技术的基础研究工作，企业主要负责产业共性技术的应用开发工作。在知识经济时代，随着市场竞争的加剧，部分产业只有突破一些关键共性技术才能实现产业转型升级，产业共性技术的研发供给不足促使研究机构和企业加大产业共性技术研发投资力度。企业为了激励研究机构研发的积极性，考虑给研究机构提供一定比例的研发投入补贴。图1描述了产业共性技术协同研发机理。

图1 产业共性技术产学研协同研发机理示意图

2.2 基本假设

该问题相关的5个假设条件如下：

1)假设企业研发努力程度为EE(t)，研究机构研发努力程度为ES(t)。则二者的研发投入为：

(1)

其中：企业的研发投入系数为μE，研究机构的研发投入系数μS；企业研发投入为IE(t)，研究机构的研发投入为IS(t)，均为关于双方研发努力程度的凸函数。

2)假设t时刻企业和研究机构技术研发程度为K(t)，技术研发是一个动态变化过程，且受企业和研究机构研发努力程度和技术更新的影响，因此参考文献[27]知识创新量随时间变化的微分方程的假设(因为技术研发的过程即是知识创新的过程，所以技术研发过程可参考知识创新过程)，企业和研究机构的协同研发过程可以表示为：

(2)

其中：在初始状态下，K(0)=K0≥0；λ1、λ2分别表示企业和研究机构研发努力程度对研发程度的影响，即研发能力系数；因为在技术研发的过程中同时也会发生技术更新淘汰，因此用δ>0表示研发过程中的技术淘汰率。

3)借鉴文献[29]产品质量管理总收益模型的思想(因为技术研发是产品质量提升的主要途径，所以技术研发努力对总收益的影响可参考质量提升努力对总收益的影响)。

假设企业和研究机构在t时刻协同研发总收益π(t)可以表示为：

π(t)=χ1EE(t)+χ2ES(t)+ηK(t)

(3)

其中：χ1为企业边际收益系数，χ2为研究机构边际收益系数，η>0为收益影响系数(技术研发对总收益的影响程度)。

4)假设企业和研究机构协同研发所得到的总收益仅在参与双方进行分配，企业收益分配系数为α(0<α<1)，研究机构收益分配系数为1-α，此分配比例由双方协定。企业给研究机构提供的研发投入补贴为σ(0≤σ≤1)。企业和研究机构均存在正贴现率ρ，且均以探求在同一无限的时空区域内自身收益最大化的研发策略为目标。

企业和研究机构的目标函数分别为：

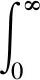
(4)

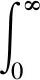
(5)

5)式(1)—(5)包含3个控制变量EE(t)、ES(t)、σ以及一个状态变量K(t)。反馈决策可以表示技术研发程度与时间之间的函数，企业的研发努力程度可以表示为EE(K(t),t)，研究机构的研发努力程度可以表示为ES(K(t),t)。由于非固定参数情形下无法对模型进行求解，继而假设模型中所有参数均为与时间无关的正的固定参数，企业和研究机构在任意时间点面对的都是同一博弈。所以将决策假定在静态决策[30]，得到相应的静态反馈均衡状态。为便于书写，以下将EE(t)、ES(t)、K(t)均简写为EE、ES、K。

3 模型构建及求解

3.1 Nash非合作研发博弈情形

在Nash非合作研发情形，企业和研究机构相互独立且地位平等，均以实现自身收益最大化为目标，双方研发收益函数分别为VE(K)、VS(K)，VE(K)、VS(K)均连续有界可微且在所有K≥0的情况下都满足HJB方程[31]：

(6)

(7)

对HJB方程右边部分进行求解，若想使其最大化需式(6)对EE求一阶偏导、式(7)对ES求一阶偏导，并假设其均得零，解得：

(8)

(9)

将式(8)、式(9)带入式(6)、(7)中并化简得：

(10)

(11)

由式(10)和式(11)可知，HJB方程的解是以K为自变量的一元一次函数式，因此令：

VE(K)=a1K+a2

(12)

VS(K)=b1K+b2

(13)

其中a1，a2，b1，b2为待求解的常数，可求得：

(14)

(15)

将式(12)、(13)、(14)、(15)代入式(10)、(11)得：

(16)

ρ(b1K+b2)=[(1-α)η-δb1]K+

(17)

根据先前VE(K)和VS(K)对所有的K≥0都满足的假设，因而a1，a2，b1，b2的值为：

将a1，b1代入式(8)，(9)可求得企业和研究机构各自最优研发努力程度分别为：

(18)

(19)

将a1，a2，b1，b2代入式(12)，(13)可求得企业和研究机构各自最优研发收益函数分别为：

(20)

(21)

根据式(20)和(21)可求得企业和研究机构最优研发总收益函数为：

(22)

3.2 Stackelberg主从研发博弈情形

在Stackelberg主从研发博弈情形，企业为研发过程中的领导者，研究机构为追随者，企业为了激励研究机构研发的积极性，给研究机构提供一定比例的研发投入补贴σ(0≤σ≤1)。在该情形下，企业先确定研发努力程度和对研究机构的研发投入补贴；研究机构获取企业的决策信息后做出相应的跟随决策以确保自身收益最大化，企业在做出决策之前可以有效预测研究机构的跟随决策。双方研发收益函数为分别为VE(K)、VS(K)，VE(K)、VS(K)均连续有界可微且在所有K≥0的情况下都满足HJB方程。根据逆向归纳法，研究机构的最优控制为：

(23)

对HJB方程右边部分进行求解，若想使其最大化需式(23)对ES求一阶偏导并假设其均等于零，解得：

(24)

企业在做出决策之前能够获得研究机构依据式(24)的跟随决策ES，因此企业根据研究机构的决策信息确定自身研发努力程度以及对研究机构的研发投入补贴来实现自身收益最大化，此时企业最优控制为：

(25)

将式(24)代入式(25)并对其右边部分进行求解，若想使其最大化需式(25)分别对EE和σ求一阶偏导并假设其均等于0，解得：

(26)

(27)

将式(24)、(26)、(27)代入式(23)、(25)化简得：

(28)

(29)

由式(28)和式(29)可知，HJB方程的解是以K为自变量的一元一次函数式，因此令：

VE(K)=a1K+a2

(30)

VS(K)=b1K+b2

(31)

其中a1，a2，b1，b2为待求解的常数，可求得：

(32)

(33)

将式(30)、(31)、(32)、(33)代入式(28)、(29)得：

(34)

ρ(b1K+b2)=[(1-α)η-δb1]K

(35)

根据先前式VE(K)和式VS(K)对所有的K≥0都满足的假设，因而a1，a2，b1，b2的值为：

将a1,b1代入式(24)，(26)，(27)可求得企业和研究机构的各自最优研发努力程度和最优研发投入补贴系数分别为：

(36)

(37)

(38)

将a1，a2，b1，b2代入式(30)，(31)可求得企业和研究机构最优研发收益函数分别为：

(39)

(40)

根据式(39)和(40)可求得企业和研究机构最优研发总收益函数为：

(41)

3.3 协同合作研发博弈情形

在协同合作博弈情形，企业与研究机构基于互补的创新资源开展协同研发，双方均以研发总收益最大化为目标，总收益函数为V(K)，V(K)连续有界可微且在所有K≥0的情况下都满足HJB方程，此时：

J=JE+JS=

(42)

(43)

对HJB方程右边部分进行求解，若想使其最大化需式(43)对EE和ES求一阶偏导并假设其等于零，解得：

(44)

(45)

将式(44)、(45)代入式(43)化简得：

ρV(K)=[η-δV′(K)]K

(46)

由式(46)可知，HJB方程的解是以K为自变量的一元一次函数式，因此令：

V(K)=c1K+c2

(47)

其中c1，c2为待求解的常数，可求得：

(48)

将式(47)、(48)代入式(46)得：

ρ(c1K+c2)=(η-δc1)K

(49)

根据先前式V(K)对所有的K≥0都满足的假设，因而c1，c2值为：

将c1代入式(44)，(45)可求得企业和研究机构各自最优研发努力程度分别为：

(50)

(51)

将c1，c2代入式(47)，可求得企业和研究机构最优研发总收益函数为：

(52)

因为企业收益分配系数为α(0<α<1)，研究机构收益分配系数为1-α，因此，企业和研究机构各自最优研发收益函数分别为：

(53)

(54)

3.4 三种博弈结果比较分析

分别比较上述三种研发博弈情形下企业和研究机构各自最优研发努力程度、最优研发收益以及双方最优研发总收益，可以得出以下结论：

命题1：在Nash非合作博弈和Stackelberg主从博弈情形下，企业的研发努力程度不发生改变；在Stackelberg主从博弈情形下，研究机构的研发努力程度相比Nash非合作博弈情形显著提高，提高水平等于研发投入补贴系数，表明研发投入补贴作为一种激励机制可提高研究机构的研发努力程度；在协同合作博弈情形下，企业和研究机构的研发努力程度均优于非合作博弈情形。

证明：由式(18)、(19)、(36)、(37)、(50)、(51)可得：

EE2=EE1，

EE3-EE2>0

ES2-ES1=ES2·σ2≥0

ES3-ES2>0

证毕。

命题2：在Stackelberg主从博弈情形下，企业和研究机构各自研发收益均优于Nash非合作博弈情形，即当企业向研究机构提供研发投入补贴时，企业和研究机构的研发收益均得到提升。

证明：由式(20)、(21)、(39)、(40)可得：

ΔVE(K)=VE2(K)-VE1(K)

ΔVS(K)=VS2(K)-VS1(K)

证毕。

命题3：在协同合作博弈情形下，企业和研究机构的研发总收益优于Stackelberg主从博弈情形；在Stackelberg主从博弈情形下，企业和研究机构的研发总收益优于Nash非合作博弈情形。

证明：由式(22)、(41)、(52)可得：

V3(K)-V2(K)

V2(K)-V1(K)

V2(K)-V1(K)

即V3(K)>V2(K)>V1(K)，证毕。

4 产业共性技术研发收益协调机制

证明：由命题3可知，在协同合作博弈情形下，企业和研究机构研发总收益实现帕累托最优。若要实现企业和研究机构在协同合作博弈情形下各自最优研发收益实现个体的帕累托最优。需要对双方的研发策略进行调整，即：

VE3(K)≥VE1(K),VS3(K)≥VS1(K)

(55)

VE3(K)≥VE2(K),VS3(K)≥VS2(K)

(56)

又由命题2可知，只需式(56)成立即可证明命题4成立。

(57)

解式(57)得：

(58)

5 数值算例分析

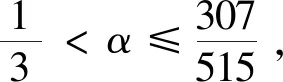
根据上述参数可得EE1=0.87，ES1=1.2，EE2=0.87，ES2=1.4，σ2=0.14，EE3=2.2，ES3=2.1，ΔVE(K)=0.57，ΔVS(K)=0.34。

图2 企业研发收益在三种不同博弈情形下的比较

图3 研究机构研发收益在三种不同博弈情形下的比较

根据图2—图4可知，企业、研究机构以及双方研发总收益均与时间正相关，且前期变化幅度大于后期变化幅度，收益水平由高到低的顺序始终为协同合作博弈情形、Stackelberg主从博弈情形、Nash非合作博弈情形，验证了命题3结论的同时，又进一步验证了命题2和命题4的结论。

图4 双方研发总收益在三种不同博弈情形下的比较

6 结语

本文引入微分博弈的方法基于动态视角对产业共性技术产学研协同研发策略及收益协调机制进行研究，运用HJB方程分别考察三种研发博弈情形下研究机构和企业各自的最优研发努力程度、最优研发收益和双方最优研发总收益以及企业对研究机构的研发投入补贴问题。通过对三种博弈结果的比较，得出以下结论：(1)研发投入补贴作为一种激励策略，可促进研究机构研发努力程度、双方各自研发收益以及双方研发总收益的提升；(2)协同合作博弈情形下双方各自研发努力程度、各自研发收益和双方研发总收益均优于非合作情形，且收益分配系数α存在一个阈值，可实现双方个体收益的帕累托改进。最后，通过数值算例分析验证了理论推导的结果。

本文后续研究可在以下几个方面拓展：(1)在本文的基础上考虑产业共性技术产学研协同研发与扩散的决策机制；(2)本文假设模型中的参数均与时间无关，今后的研究可以考虑在与时间相关参数的情况下对模型进行求解；(3)考虑政府对产业共性技术产学研协同研发的影响机理；(4)鉴于合作博弈可以增加个体和体系的收益，今后的研究可以考虑运用效用理论对合作博弈下的收益增量进行划分。