解线性最小二乘问题的2 个混合交替CQ 算法

付元敏， 朱立军， 贺 龙

（北方民族大学 数学与信息科学学院，宁夏 银川750021）

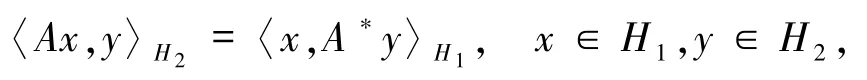
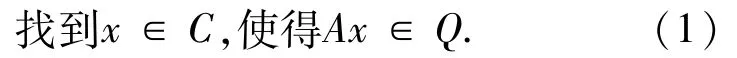
总是假设SFP（1）是有解的和Ω 代表SFP（1）的解集，即

这个问题出现在相位恢复、信号工程、图像重建等领域，参见文献［2 -4］.为了解决分裂可行性问题，2004 年，Byrne［3］给出了一个CQ算法如下：

接下来的问题叫做多集分裂可行性问题（MSSFP），它被发现应用在强度可调放射疗法中，已经被许多学者研究［5-9］：分别给出H1和H2的闭凸子集

和有界线性算子A：H1→H2，找到点使得总是假设多集分裂可行性问题是有解的，为了解决这个问题，Censor 等［6］提出了如下算法：

PC和PQ分别代表C 和Q上的正交投影，也就是说PC（x）使｛‖c -z‖，c∈C｝取得最小值，其中‖·‖代表2 -范数.

为了解决分裂等式问题，Moudafi［10］提出了如下的交替CQ算法：

2013 年，Byrne 等［11］提出了如下投影Landweber算法研究分裂等式问题：

2016 年，Chuang 等［12］提出了如下混合交替CQ算法解决分裂等式问题：

受到以上研究的启发，本文给出2 个改进的混合交替CQ算法来研究线性最小二乘问题.

1 预备知识

本节给出一些基本的定义和引理.令H是实的希尔伯特空间赋有内积〈·，·〉和范数‖·‖的性质.接下来介绍一些记号.

（ii）‖x+y‖2=‖x‖2+‖y‖2+2〈x，y〉和‖x-y‖2=‖x‖2+‖y‖2-2〈x，y〉；

（iii）〈x+y，x-y〉=‖x‖2-‖y‖2；

（iv）‖x+y‖2≤‖x‖2+2〈x+y，y〉；

（v）‖αx +（1 -α）y‖2=α‖x‖2+（1 -α）‖y‖2-α（1 -α）‖x-y‖2，∀x，y∈H，∀α∈［0，1］.

定义1.1三角不等式性成立：

定义1.2T：H→H是Lipschitz连续的，如果

对于正的常数κ 成立，κ 是Lipschitz 常数.也说T是κ-Lipschitz连续的.

定义1.3令C 是H 的非空闭凸子集，T：C→C是非扩张映射，如果‖Tx - Ty‖≤‖x - y‖， x，y ∈C.

引理1.4［12］令｛ρn｝n∈N是在（0，1/max｛‖A‖2，‖B‖2｝）中的序列，使得文献［12］中的（2.34）式成立并且假设

或

那么文献［12］中的算法2.2 产生的序列｛（xn，yn）｝n∈N存在使得和¯，n→∞.

引理1.5［13］假设f：Rn→R是一个有限凸函数，那么它是处处次可导的并且在Rn的任意有界子集上是一致有界的.

引理1.6［14］令K是希尔伯特空间H的非空闭凸子集，｛xn｝是在H里的序列满足如下性质：

（ii）ωω（xn）⊂K，

那么，｛xn｝弱收敛到K中的一点.

引理1.7［15］令C是实的希尔伯特空间H的非空闭凸子集，PC是H到C的度量投影，那么

（i）〈x-PCx，PCx-y〉≥0 对于所有的x∈H，y∈C成立；

（ii）‖x-PCx‖2+‖PCx-y‖2≤‖x-y‖2对于所有的x∈H，y∈C成立；

（iii）‖PCx -PCy‖2≤〈x -y，PCx -PCy〉对于所有的x，y∈H成立.

引理1.8［5］假设0 ＜γ ＜2/L，其中L 是文献［5］的（3.2）中定义的，当MSSFP 有解时由文献［5］的算法（3.1）产生的序列｛xn｝弱收敛到MSSFP的解z，同时z也是函数p在Ω上的最小值.

为了解决SFP定义如下逼近函数

f（x）的梯度函数是

请参见文献［21］.

2 主要成果

令H1、H2、H3是实的希尔伯特空间赋有内积〈·，·〉H1和范数‖·‖Hi的性质，内积和范数简记为〈·，·〉和‖·‖.C、Q 分别是H1和H2的非空闭凸子集.A：H1→H2是有界线性算子和A*是其共轭算子.令δ∈（0，1）.Ω =｛x∈C：Ax∈Q｝=C∩A-1Q是分裂可行性问题和多集分裂可行性问题的解.假设借助引理1.4 得到定理2.1 和定理2.3.｛ρn｝n∈N是在（0，∞）中的序列.现在给出如下算法研究（SFP）.

算法2.1给定x0∈H1，借助下面迭代步骤找到近似解.

步骤1 计算（un，vn）：

步骤3 计算（xn+1，PQAxn+1）：

接下来，更新n：n+1 和回到步骤1.

注2.1如果

那么（8）式成立.

证明不失一般性，假设xnun，PQAxnvn，有

定理2.1令｛ρn｝n∈N是在（0，1/max｛‖A‖2，1｝）中的序列使得（8）式成立，假设

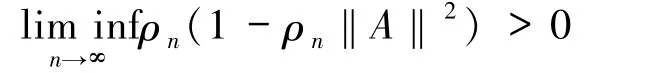
或

那么算法2.1 中的序列｛（xn，PQAxn）｝n∈N存在使得和

证明取n∈N 并令n 固定，取任意的∈Ω并令）固定，那么有首先设

那么

由（9）式可得

然后借助引理1.7 可得

因此，由（11）和（12）式得

由（13）和（14）式有

接下来有

由引理1.7 有

和

所以，由（16）～（19）式可得

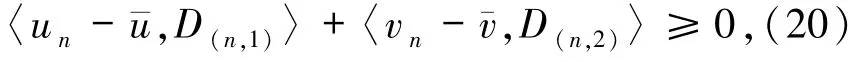
其显示

借助（9）、（15）和（21）式得

并且有

其显示

因此，由（25）式得到

借助（23）和（26）式可得

由引理1.7 有

同理，

同理，

借助（28）～（31）式可得

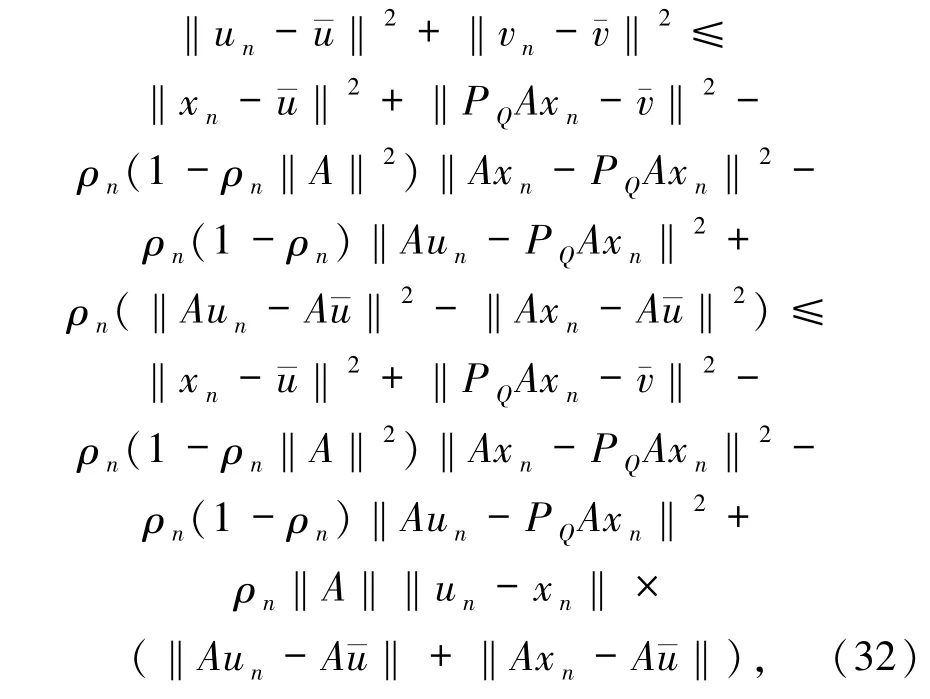
得到

由（27）和（35）式得到

｛xn｝n∈N和｛PQAxn｝n∈N是有界序列，存在｛xn｝n∈N和｛PQAxn｝n∈N的子序列｛xnk｝k∈N和｛PQAxnk｝k∈N使得和

此外

和平方范数的下半连续性有

和

显然

存在.因此，由（38）式可得

同理由（39）式可得

注记2.2假设｛ρn｝n∈N满足如下不等式：

那么｛ρn｝n∈N满足定理2.1 的条件.

为了解决多集分裂可行性问题（MSSFP）定义逼近函数

g（x）的梯度函数是

令Ω=｛x∈C：Ax∈Q｝=C∩A-1Q是多集分裂可行性问题的解集并且假设给出如下算法研究多集分裂可行性问题.

算法2.3给定x0∈H1，找出如下迭代步骤的近似解.

步骤1 计算（un，vn）如下：

步骤3 计算（xn+1，PQAxn+1）如下：

接下来，更新n：n+1 和回到步骤1.

定理2.3令序列｛ρn｝n∈N满足

且假设

或

那么算法2.3 中序列｛（xn，PQAxn）｝n∈N存在是（MSSFP）的解，即¯ 和→∞.

证明取n∈N且令n固定.取且令）固定，那么和首先，设

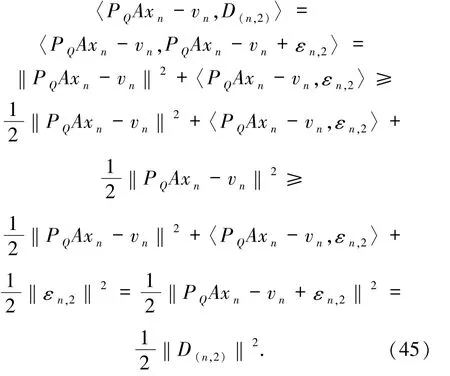
由（45）式有

由引理1.7 得到

所以，由（47）式得

由（48）式可得

接下来有

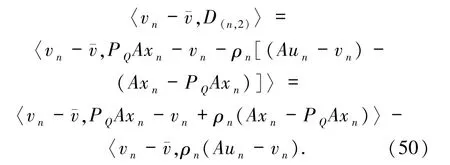
由引理1.7 得

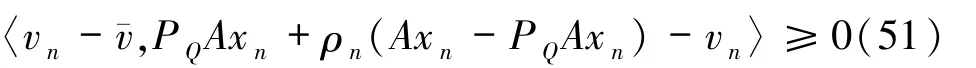
和

所以，由（50）～（52）式可得

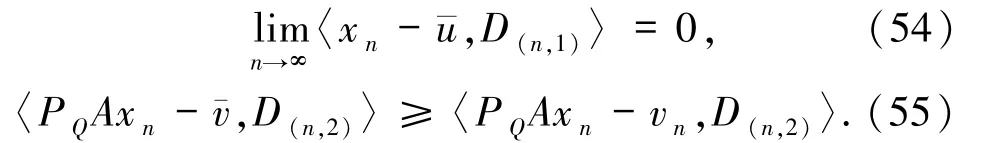
由（45）、（49）和（55）式

由

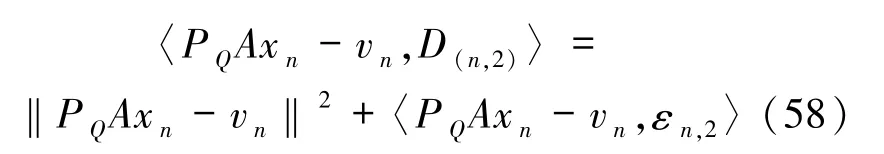
可得

因此，由（59）式得到

由（57）和（60）式可得

由引理1.7 有

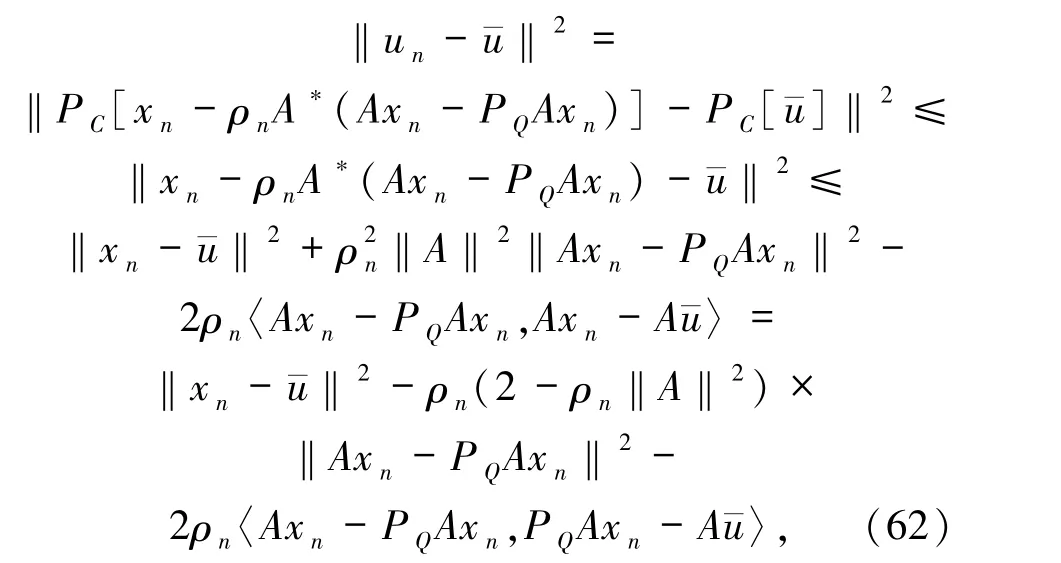
同理，

可得到

由（62）～（65）式得

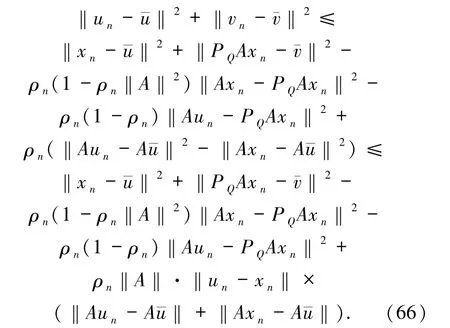
可得到

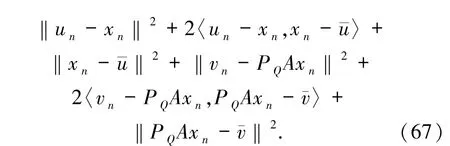
由（61）和（69）式得到

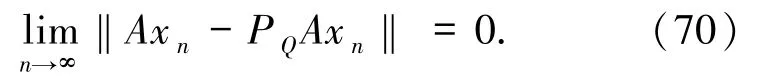
由｛xn｝n∈N和｛PQAxn｝n∈N是 有 界 序 列，存 在｛xn｝n∈N和｛PQAxn｝n∈N的子序列｛xnk｝k∈N和｛PQAxnk｝k∈N使得

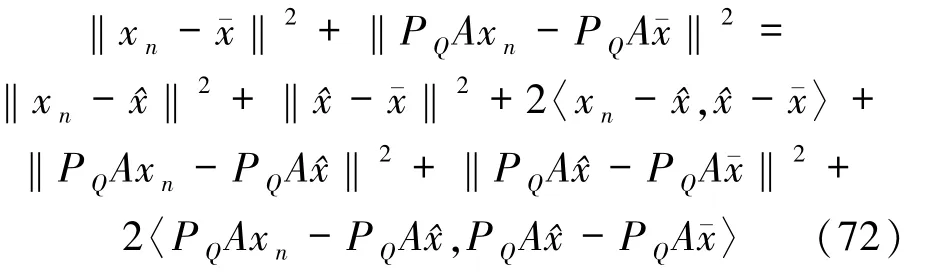
和

显然

存在.所以，由（72）式可得

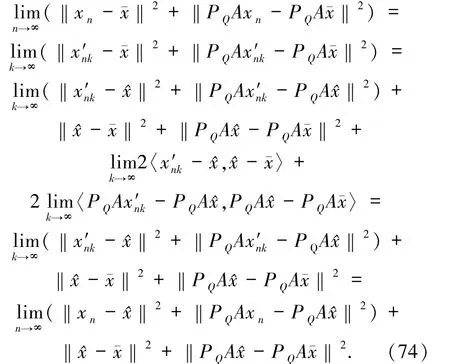
同理，由（73）式可得

3 应用

3.1 线性最小二乘问题给出线性方程Ax =b，其中A是m×n矩阵，x∈Rn，b∈Rm.问题

叫做线性最小二乘问题（LLSP）.这个问题等价于ATAx=ATb.为了解决LLSP定义如下逼近函数

h（x）的梯度函数是

ai是A 的行，即，b =（β1，…，βm），ai∈Rn，βi∈R，i∈I =1，2，…，m.给出如下算法解决（LLSP）：

算法3.1给定x0∈H1，找到下列迭代步骤的近似解：

步骤1 计算un如下：

步骤3 计算xn+1如下：

接下来，更新n：=n+1 和回到步骤1.

借助定理2.3 得到如下定理解决线性最小二乘问题.

定理3.1给定b∈H2，δ∈（0，1）.令Ω2是（V）的解，假设令｛ρn｝n∈N满足以上条件并假设

或

那么，算法3.1 中的序列｛xn｝n∈N存在使得

4 结束语

本文给出2 个混合交替CQ算法解决分裂可行性问题和多集分裂可行性问题.给出弱收敛证明并把它们应用求解线性最小二乘问题.