广义神经传播方程的Wilson 元收敛性分析

梁聪刚， 张厚超， 石东洋

（1.平顶山学院 数学与统计学院，河南 平顶山467000； 2.郑州大学 数学与统计学院，河南 郑州450052）

神经传播过程中，神经传播信号及它关于时间和空间的变化率，在数学上表现为一类非线性拟双曲方程［1］

其中，Ω∈R2是矩形区域，∂Ω 为其光滑边界，X =（x，y），u0（X）及u1（X）是已知光滑函数，f（u），g（u）及其偏导数对变量u满足Lipschitz连续.

非线性拟双曲方程是近年来发展起来的一类重要的非线性发展方程，它在生物、力学等领域有着广泛的应用［2］.文献［3］研究了该类方程初边值问题解的长时间行为.文献［4］对高维广义神经传播方程的整体光滑解进行了研究.文献［5］给出了全离散的Galerkin近似.文献［6 -7］讨论了该类方程的A.D.I.有限元方法和特征差分法.文献［8 -10］分别利用双线性元，Hermite 型矩形元和类Wilson元得到了该类方程的超收敛和外推结果.文献［11］应用Crouzeix -Raviart 非协调线性三角形元得到了变网格下的最优误差估计.文献［12］考虑了该类方程的各向异性非协调有限元的超收敛分析.文献［13 -14］研究了混合有限元格式，得到了半离散格式下的最优误差估计.文献［15］利用EQrot1元及零阶R-T元建立一个低阶非协调混合元格式，得到了超逼近结果.然而，我们发现上述文献提高收敛阶的方法大多是利用插值后处理技术，外推或者构造新的单元.文献［16 -17］在研究二阶抛物和椭圆问题时，借鉴了文献［18 -19］的思想方法，利用内部惩罚方法构造了一个新的离散变分形式，并在双线性型中添加了稳定项，使得Wilson元相容误差项变成了0，收敛阶提高到O（h2）.

本文的主要目的是将文献［16 -17］的思想应用于问题（1）的收敛性研究.首先，证明了半离散格式逼近解的存在唯一性.其次，利用Wilson 元在新范数意义下的插值估计和双线性型的性质导出了半离散格式下原始变量u 在新范数意义下O（h2）阶的收敛结果.最后，通过构造一个二阶的全离散格式，得到了相应的O（h2+τ2）阶高精度结果，这是文献［16 -17］未涉及的.

本文中，Ws，p（D）（D⊂Ω）表示通常的Sobolev空间，‖·‖s，p，D和｜·｜s，p，D分别表示其上的范数和半范，其中s为非负整数，1≤p≤∞.当p =2 时，记Ws，2（D）= Hs（D），‖·‖s，D和｜·｜s，D分别表示Hs（Ω）上的范数和半范，当D =Ω时，省略下标D.约定

其中X为Banach空间.本文中，C 是与h 和τ 无关的正常数，在不同的地方取值可以不同.

1 单元的构造及性质

设εh表示所有单元边界所成的集合，E表示单元边界，hE表示E的长度.规定函数f 在相邻单元K和K′的相交边上的跳跃值和平均值分别为

Wilson元的形函数空间为P2（K），有限元空间为定义在Ω上，vh｜K∈P2（K），vh在内节点处连续，在边界∂Ω上节点处为0｝，其中vh｜K由4 顶点函数值以及和确定.

定义Vh上的模和双线性型［16］分别为

其中

α是待定常数.显然有‖vh‖0≤C‖vh‖h成立.Ih：H2（Ω）→Vh为相应的插值算子.

文献［16 -17］已证明如下3 个结论.

引理1.1设u∈H3（Ω），则有

引理1.2设｛Γh｝是区域Ω的正则矩形剖分，即存在σ ＞0，使得∀K∈Γh，有.则存在0，使得

引理1.3是连续的，V-椭圆的双线性型，则，使得

2 半离散格式的收敛性分析

与（1）式等价的变分问题为：求u∈H10（Ω），使得

（4）式的传统半离散格式为：求uh∈Vh，使得

为提高逼近精度，我们引进新的半离散格式为：求uh∈Vh，使得

定理2.1问题（6）存在唯一解.

证明设是Vh的基函数，则

其中L0，L1是已知的，由

决定，

从而（7）式是关于向量函数L（t）的一个常微分方程组.根据常微分方程的理论，注意到A 是正定对称矩阵，对于给定初值L（0），L′（0），它的解是唯一存在的.因而问题（6）的解存在唯一.证毕.

下面先讨论上述问题的收敛性.

定理2.2设u、uh分别是（1）和（6）式的解.设u，ut∈H3（Ω），utt∈H2（Ω），则有

证明令由于u∈H3（Ω），则有

根据（1）和（6）式有下面误差方程

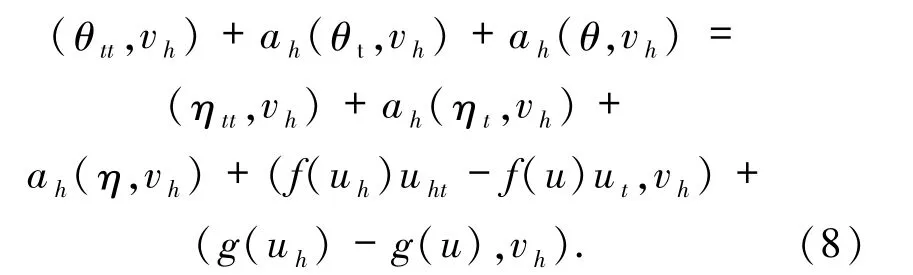
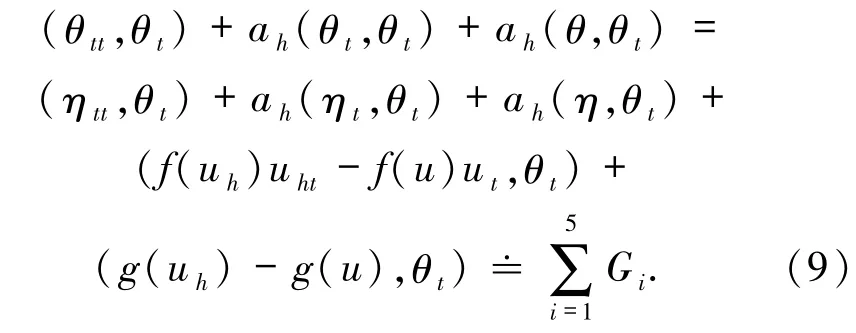
首先注意到

下面对Gi（i=1，2，…，5）进行估计.

将Gi（i =1，2，…，5）的估计及（10）式代入（9）式，则有

对（11）式两边对变量t 从0 到t 求定积分，注意到θ（X，0）=0，θt（X，0）=0，则有

由文献［16］知（12）式左端可化为

即

因此

证毕.

3 全离散逼近格式的收敛性分析

在本节中，将给出问题（4）的全离散逼近格式及相应的误差估计.将时间区间［0，T］进行N 等分，即，则时间步长τ =在Vh中的逼近，对于［0，T］上的任意光滑函数ψ，定义

建立（4）式的全离散逼近格式如下：求Un∈Vh，使得

定理3.1设un、Un分别是（1）和（13）式的解，若

则有

证明令

由（1）和（13）式得误差方程为

其中，

首先注意到

下面对Bi（i=1，2，…，7）进行估计.

将（16）～（24）式代入（15）式，两边同乘2τ，再关于n从1 到J-1（J≤N）求和，得

再利用

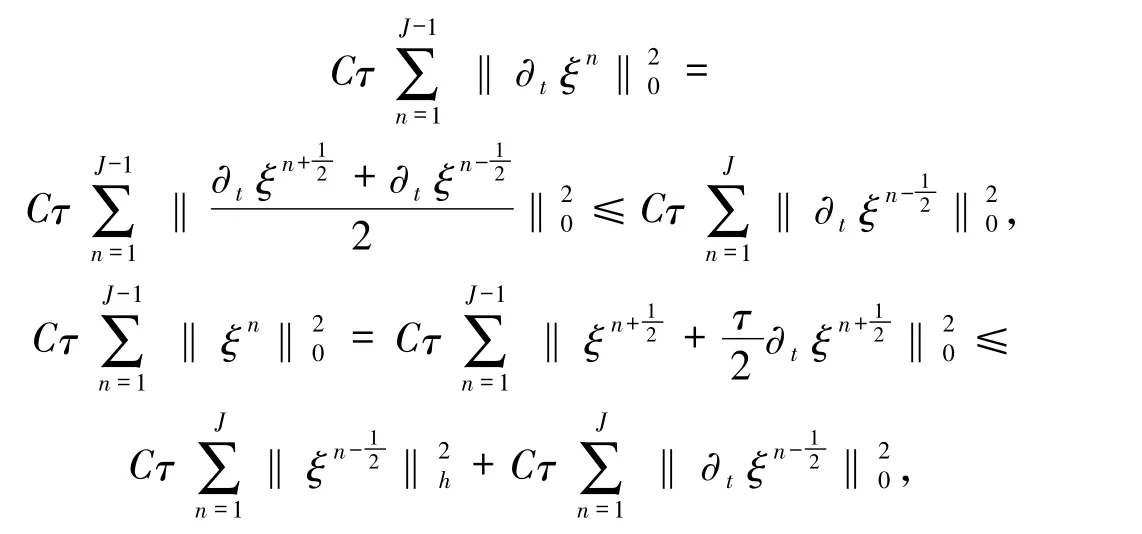
则有

下面来估计上式右端后两项.利用泰勒公式有

从而

所以

将（27）和（28）式代入（26）式，当1 -Cτ ＞0 且Cτ ＞0 时，利用离散的Gronwall引理有

因此

证毕.

4 结论

本文通过引入新的双线性型，对广义神经传播方程分别构造了一种新的半离散格式和全离散格式，并且在比传统的能量模更大的范数意义下，得到了相应的比通常估计方法高一阶精度的收敛结果.在整个分析过程中，对（18）式的估计起到了关键作用.本文对其他偏微分方程的数值求解提供了可借鉴的思路和途径.