小议二次函数问题中的“降维打击”

广东省东莞市黄江中学

二次函数问题是数学中考的热点对象，在历年各地的中考题里面求满足具体条件的点的坐标问题经常出现.该类问题设计情景丰富，问法多种多样，部分学生面对这类问题时会对情景理解感到困难，或者分析不出解决问题的关键，使这部分学生产生畏难情绪，放弃得分.其实我们可以在一些中考题中得到一些启发，这些二次函数中的问题其实可以通过“降维打击”来解决.下面就从三个例子来说明.

例1(2018年黑龙江中考数学试题) 如图1，抛物线y=x2+bx+c与y轴 交于点A(0,2)，对 称轴为 直 线x=-2，平行于x轴的直线与抛物线交于B,C两点，点B在对称轴左侧，BC=6.

(1)求此抛物线的解析式.

(2)点P在x轴上，直线CP将ΔABC面积分成2: 3两部分，请直接写出P点坐标.

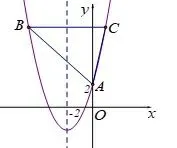
图1

图2

分析第一小问：易得二次函数解析式为y=x2+4x+2.

第二问：若学生设点P的坐标，然后求出直线CP与AB的交点，来迎合题目的条件，这样十分费时费力，效果不理想.其实我们可以引导学生先根据对称轴x=-2和BC=6 等条件求出点B(-5,7),C(1,7)，再从面积条件入手，利用面积比在直线AB上找到一个辅助点M(如图2)，如何得到M的坐标呢？ΔBCA与ΔBCM同底，直线CP将ΔABC面积分成2: 3 两部分，从而得BM:AB=2: 5或BM:AB=3: 5，于是我们可以过点M向BC或者y轴作垂线，求出对应垂线段长度，得点M的纵坐标或者横坐标，利用直线AB的解析式，求出点M的坐标为(-2,4)或(-3,5)，再求出直线CM解析式，就能求出点P的坐标.我们可以看出第二问中多次利用线段长度和直线解析式，体现了转化思想的运用，让学生知道寻找合适的辅助点或辅助线来帮助解决问题.

例2(2018年广东中考数学试题) 如图3，已知顶点为C(0,-3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点，直线y=x+m过顶点C和点B.(1)求m的值；(2)求函数y=ax2+b解析式；(3)抛物线上是否存在点P使得∠PCB=15°?若存在，求点P坐标；若不存在，请说明理由.

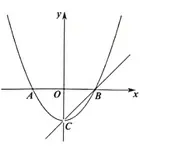
图3

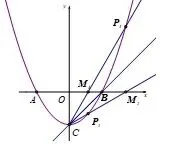
图4

第一小问：由点C(0,-3)在直线y=x+m即可得m=-3；

第二小问：将B(3,0),C(0,-3)代入y=ax2+b中，得二次函数的解析式为

第三小问：部分学生会对∠PCB=15°这个特殊的条件感到疑惑，努力在脑海中搜索关于15°的知识，不得其解.实际上一些脑筋较灵活的学生会想到15°正好是我们常见的30°，45°，60°这三个特殊角度的差.哪里找到这些角度呢？我们可以从点B,C的坐标得OB=OC，就出现了等腰直角三角形OBC，∠BCO这个45°角就出现了，将CB绕点C顺时针或逆时针旋转15°与x轴交点M(如图4)，于是我们这个问题也需要借助辅助点M和辅助线CM，只要根据条件把点M坐标和直线CM的解析式，最后联立直线CM和二次函数解析式就可求得点P的坐标.

例3(2016年深圳中考数学试题) 如图5，抛物线y=ax2+2x-3与x轴交于点A,B两点，且B的坐标为(1,0).

(1)求抛物线的解析式和点A的坐标；

(2)如图6，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

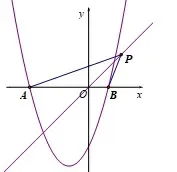
图5

图6

图7

分析第一小问：由点B(1,0) 易得抛物线解析式为y=x2+2x-3，再得点A坐标为(-3,0)； 第二小问：这个问题情境对学生来说并不“友好”，函数问题涉及角度问题，通常都会令学生难易入手.如何将角的问题转化为常见的直线问题是关键，这将考查学生的综合能力.该问题仍然需要辅助点和辅助直线，假定直线y=x上存在点P使∠APO=∠BPO，即直线y=x平分∠APB,我们可以想到会出现两种情况，如图6，图7.在图6的情况中，直线AP与y轴交于点M1，直线BP与y轴交于点M2，易证ΔOPM1∽= ΔOPB，于是OM1=OB=1，所以点M1坐标为(0,1)，接着利用点A、点M1求出直线AM1的解析式，直线AM1与直线y=x的交点即为所求的点P.我们也可以从M2出发，运用相同的方法求出点P的坐标.

在图7的情况中，仍然会有ΔOPM1∽= ΔOPB,∠BPO=∠M1PO,显然∠OPA ＞∠OPM1，而∠OPA ＞∠OPB不合题意，所以该情况舍去.

上述几个例子我们可以看出，中考考查学生的综合运用知识能力，会在常规的知识上套一层应用情景的外衣，使问题增加了不少的难度.通过上面3个中考题目的分析，我们需要引导学生总结规律，将这些难题“降维打击”，把“高阶问题”转化为“低阶问题”.首先，遇到不熟悉的问题情景，不要慌张，总有方法解决，可以大胆假设，细心分析，要善于发现题目当中的隐含条件，在函数作为背景的大环境中，通常都需要从题目条件中得到一些有价值的点，得到一些线段的长度，于是可能会出现相等的线段，相等的角，全等三角形，相似三角形等隐含条件，为问题的转化提供支持.

再者，这类问题的解决离不开数形结合思想，一些常见解题思路可以适当使用.这里举三个例子：(1) 将“一般转特殊”，如例2中15°角的出现是15°,45°,60°这三个常见特殊角度的差；(2)“高阶条件”转“低阶条件”，如例1中三角形的面积之比转化为高之比，实现了“二维”转“一维”；(3) 图形分析离不开“点、线、角、三角形”条件的相互转化，如例2中从点O,B,C的坐标得OB=OC，再得等腰ΔOBC，最后得45°角，再如例3中从条件中易得ΔOPM1∽= ΔOPB，再得OM1=OB=1,最后得点M坐标为(0,1)，这样的思路链条十分常见，更加值得让学生掌握.

最后，本人认为上述的思路不仅适用于二次函数问题中，还可以拓展于其他的函数的解决.数学思想中的转化思想是数学思维皇冠上的宝石，我们如何才能更接近，是师生们不断孜孜追求的目标.“降维打击”也是着重于引导学生总结转化规律，坚定信心更好地应对复杂的问题情境.