三维位势问题的梯度边界积分方程的新解法1)
董荣荣 张 超 张耀明
(山东理工大学数学与统计学院,山东淄博 255049)
引言
科学与工程领域中许多问题,例如,稳定热传导、弹性杆件的扭转、稳定渗流、动水压力、薄膜平衡、Helmhotz 方程、电磁场、非均质材料及非线性问题等[1-3],的数值分析可直接地或者间接地归结为Laplace 或Poisson 方程的边值问题的求解.边界元法是求解此类问题的强有力的数值工具.
物理量梯度边界积分方程由物理量边界积分方程关于空间变量取导数获得[4],它对于某些问题,如裂纹问题、波散射问题、薄板弯曲问题及具有退化边界的狭窄和薄域问题等[5-7],是非常有用的,因为此时仅由基本物理量的边界积分方程无法准确地表示原边值问题的解,即与原边值问题不等价.为了避免出现这种情况,通常将基本物理量的梯度边界积分方程与物理量边界积分方程组合,即对偶边界积分方程,来表示原边值问题的解.位势问题的位势梯度边界积分方程已收到了许多研究[8-12].文献[8]建立了二维位势问题的直接变量规则化梯度边界积分方程,文献[9]建立了三维位势问题的直接变量规则化梯度边界积分方程.两个梯度方程中,超奇异积分的规则化形式是相似的,即
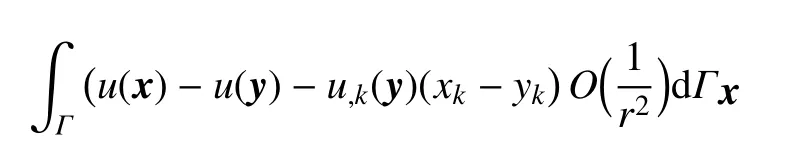
需指出的是,u,k(y)既不是已知量,也非未知量,数值实施时需将u,k(y)沿曲面(曲线)的两个(一个)切线方向及法线方向进行分解,切线方向的量采用插值逼近,法线方向的量作为未知量,因此这个积分在高价曲面单元下的数值实施是非常复杂和困难的.文献[10]研究了二维位势问题的位势梯度边界积分方程.引入一系列变换将梯度边界积分方程转换为具有强奇异积分的自然边界积分方程,然后采用加减技术规则化强奇异积分.方法有效地消去了奇异性,取得了很好的数值结果,但很难推广到三维位势问题.文献[11-12]建立了三维位势问题的间接变量规则化梯度边界积分方程,给出了高阶单元下的数值实施方案,取得了准确的数值结果.方程中规则化积分形式是
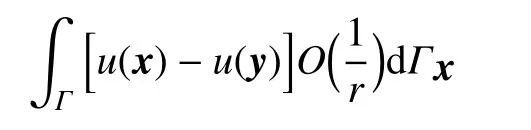
它比直接法中的形式简单得多,数值实施也容易得多.但是,其数值实施也需要许多技术性措施[11-14].不同于前述的规则化边界积分方程法,文献[15-17]和文献[18-21]分别提出了直接计算梯度方程中的奇异积分的局部规则化方法.它们的优点是算法具有一般性,可计算任何阶的奇异积分.缺点是两种算法的理论推导是繁复的,计算量也相当大,因为它们需将积分核中的每个依赖于单元参数的函数表示成在内蕴坐标系统下的局部距离ρ 的幂级数.此外,还有一些别的直接计算方法[22-26],都属于局部法,涉及与局部单元参数有关的操作.
本文提出了求解三维位势问题的位势梯度边界积分方程的新算法.该方法通过构造辅助边值问题来计算梯度边界积分方程中的系统矩阵,算法实施中不需要建立规则化边界积分方程也不需要直接计算强奇异积分.因此,方法具有数学理论简单、计算效率高、结果精度高等优点.需要强调的是,本文辅助边值问题法为梯度边界积分方程中的强奇异积分计算提供了一个新的思路和途径.另外,本文方法可以拓展到其他问题,如弹性力学问题、Stokes 及Helmholtz 问题等.
1 问题描述
本文设Ω 是示R3中的一个有界区域,Ωc是它的补域,Γ 是它们的边界.n=(n1,n2)是区域Ω 的边界Γ 在x点处的单位外法向量.三维位势问题的基本解是
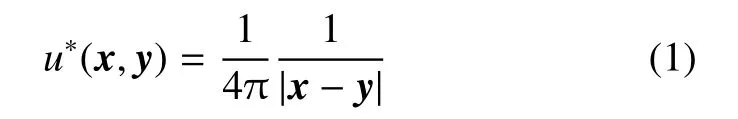

具有边界条件
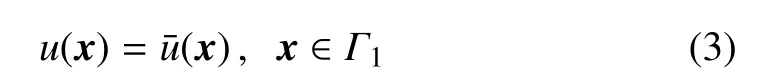
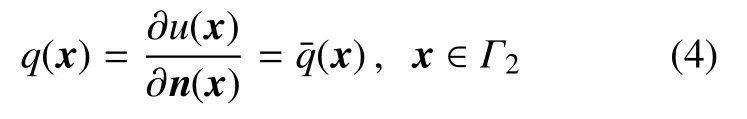
这里Γ=Γ1∪Γ2且Γ1∩Γ2=φ;是边界Γ 上已知的函数.
引理[27-30]设ψ(x)∈C0,α(Γ)和是曲面Γ 上的任一光滑点,当时,令,和假设(K1是一个常数),那么有
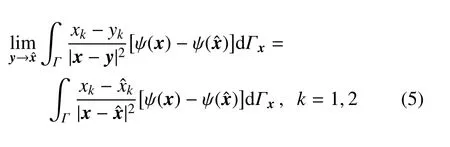
2 位势梯度边界积分方程的辅助边值问题法
2.1 边界积分方程
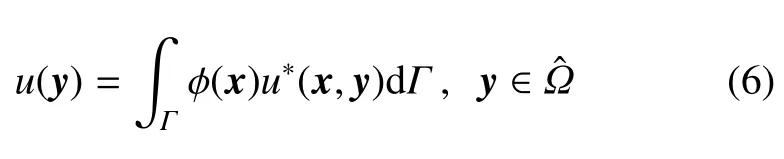
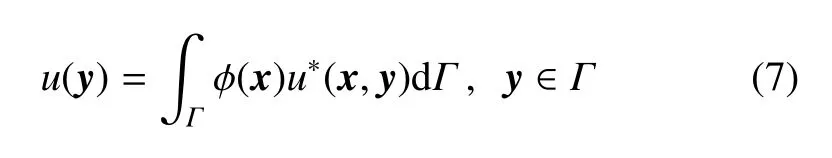
现在从式(6)出发,导出位势梯度边界积分方程.对任一个给定点,由式(6)可得


2.2 八节点四边形二次单元
边界元法的实施包括边界几何的描述和边界函数的插值逼近.为了一般性,本文采用八节点四边形二次单元来描述边界几何,八节点二次不连续插值函数来逼近单元上的边界函数.
八节点四边形二次单元的形函数Nk(ξ1,ξ2)(k=1,2,···,8)是

这里ξ1,ξ2是无因次坐标,且-1 ≤ξ1,ξ2≤1.因此单元上的点x可以近似地表示为
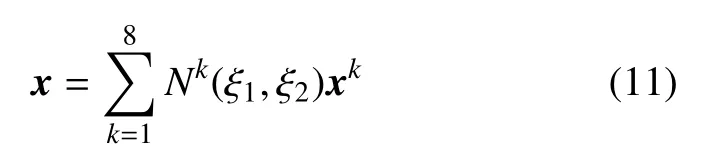
这里xk是第k个插值节点的坐标.
单元上的边界量由八节点二次不连续插值函数来逼近,即
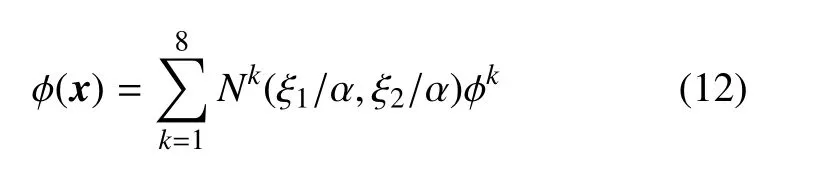
这里φk是边界函数在第k个节点处的函数值,α ∈(0,1)的常数,本文取参数α=2/3.
2.3 精确单元
许多情况下,边界几何具有参数表示.此时采用精确单元计算,可减少误差.精确单元的概念最早是本文作者2004 年提出的[27],后来许多学者跟随了这个方法,甚至赋予一个新的名字,但本质是一样的.
在三维空间中,多数情况下,固体模型的表面可以表示成参数形式

这里a,b,c,d都是有限数.当区间[a,b]和[c,d]分别被离散成N1和M1个子区间后,相应的曲面被离散成N×M个所谓的单元.由于这样的分割是在参数空间内,对应的几何点仍然在原来的曲面上,因此称为精确单元.在每个精确单元上,参数θ,φ 可表示为
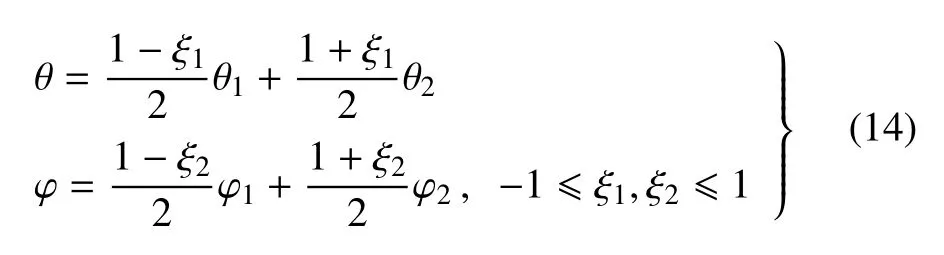
这里θi,φi(i=1,2)是精确单元的端点坐标.
2.4 边界积分方程的离散化
将边界Γ 离散成Ne单元,因而有8 ×Ne个边界节点:xi,i=1,2,···,8 ×Ne.方程(7)和(9)中的y取为任一场点xi∈Γα(属于第α 个单元),那么方程(7)和(9)的离散化形式是

2.5 辅助边值问题法
数值实施中,确定式(16)中的Ai是一个困难的问题.Ai对应离散系统矩阵中的对角元,并且对角占优,因此Ai的准确与否对解系统的性能及解的精度影响特别大.另一方面,估计Ai需要计算一个强奇异积分,其强奇异核函数是基本解关于坐标变量的偏导数,一般不是边界法向导数,因此它的计算是相当困难的[11-12].采用规则化边界积分方程可避免直接计算此类积分[11-14],但规则方程的形式较复杂,程序设计难度较大;直接计算此类积分需要繁复的理论推导和计算工作量[15-21].本文提出计算式(15),式(16)对应的系统矩阵[Gjl]和[Qjl]的辅助边值问题法.构造辅助超定边值问题,求解此边值问题可求得[Gjl]和[Qjl].下面给出具体实施过程:
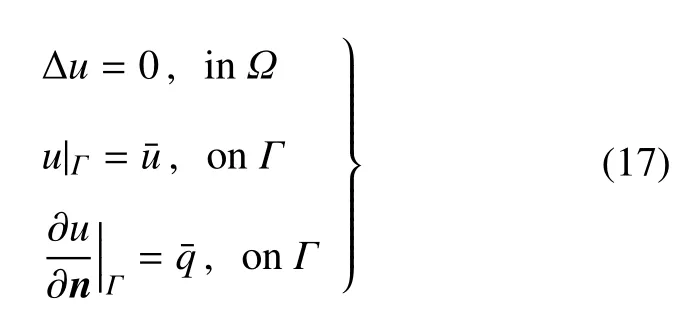
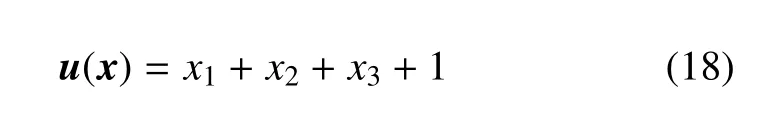

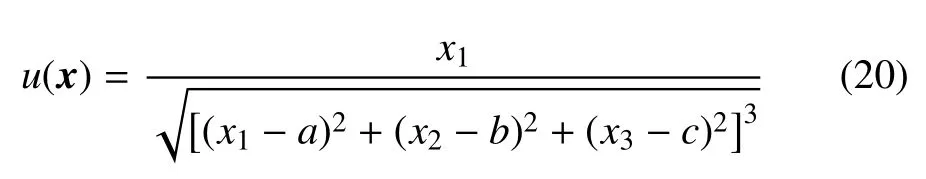
这里(a,b,c)是Ωc外的任一点.
现在用式(15)和式(16)求解边值问题(17)或(19),就可获得[Gjl]和[Qjl].值得注意的是,在求出这两个矩阵后,使用式(15)和式(16)求解有限域Ω 或者无限域Ωc上的任何边值问题,不再需要计算[Gjl]和[Qjl].由此可看出,辅助边值问题法的效率并不差.
3 数值算例
考虑3 个数值算例,来验证方法的有效性.数值实验的重点在于考察辅助边值问题法计算边界通量∂u/∂x1的能力及准确性.为了估计数值误差,采用如下L2范数
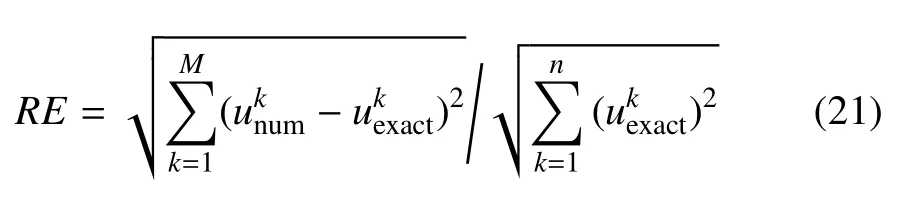
其中,M表示计算点数,分别是第k个计算点处的精确解和数值解.REu,REq及REq1分别表示边界位势u、法向梯度q=∂u/∂n及热流通量q1=∂u/∂x1的平均相对误差.
算例1作为第一个算例,考虑立方体区域Ω={(x1,x2,x3)∈R3:0 ≤x1,x2,x3≤1}上的热传导问题,如图1 所示.边界条件如下
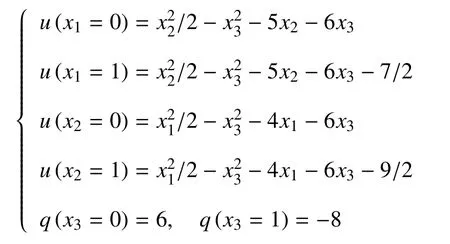
这是文献[11]采用的算例,文中没有给出边界量的计算结果,因而这里不便于比较.立方体的边界划分为54 个四边形线性单元,每一正方形表面划分9 个单元,如图1 所示.图2 给出了x3=1 面上的直线x1=11/18 上的9 个边界节点处的温度u和热通量q1=∂u/∂x1的数值计算结果,可看出,数值解和精确解吻合的很好.此外,在立方体内部选取400 个均匀分布在区域{0.15 ≤x1,x2≤0.85,x3=0.5}上的计算点,图3(a)和图3(b)分别展示了400 个计算点上的温度u和通量q1=∂u/∂x1数值解的相对误差曲面.
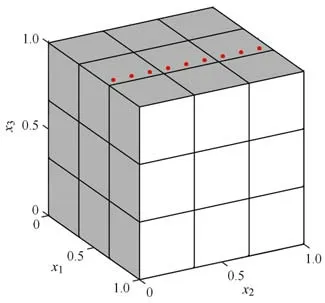
图1 边界网格及边界计算点Fig.1 Boundary grid and boundary calculation points
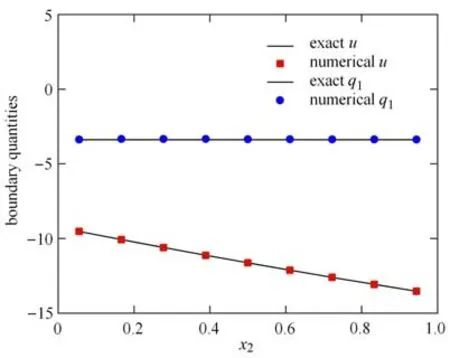
图2 图1 中9 个边界点处的温度u 和通量q1Fig.2 Temperature and flux at 9 boundary points shown in Fig.1
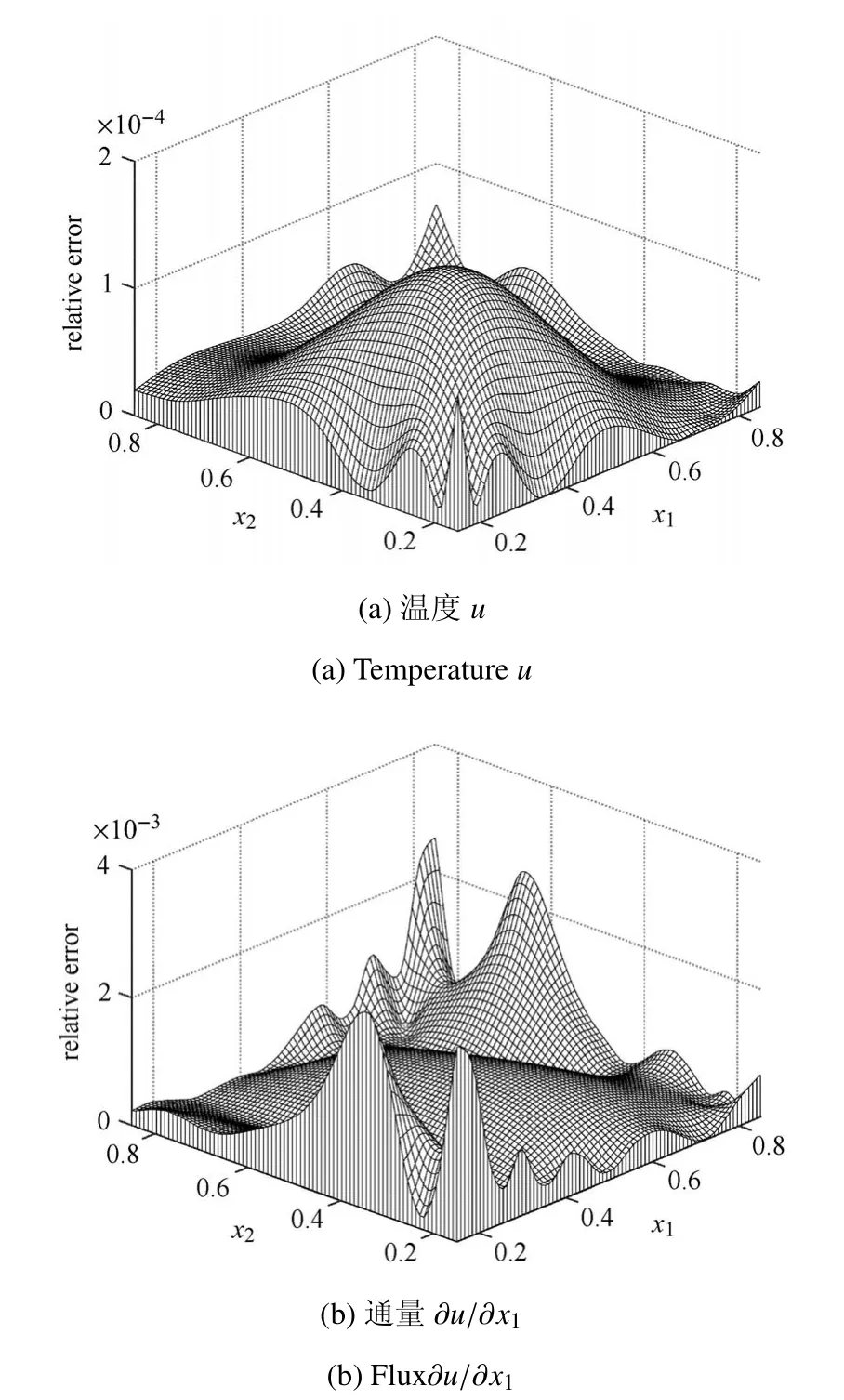
图3 场温度和通量的相对误差曲面Fig.3 Relative error surfaces for temperature and flux
算例2为了与文献[11]提出的规则化边界元法进行比较,本算例采用文献[11]中的算例.考虑单位球上的热传导,如图4 所示.问题具有Dirichlet 边界条件:u(r,φ,θ)|Γ=,其中由下列问题的解析解给出

在单位球内部选择400 个计算点,均匀分布在球面(根据θ,φ)上.图5 描述了这400 个计算点上的场温度u和场梯度∂u/∂x1数值解的L2误差随边界单元数增加的变化情况,即收敛曲线.表1 列出了本文方法与规则化边界积分方程法[11]在不同单元数下,求得的边界位势梯度q=∂u/∂x1和法向梯度q=∂u/∂n数值解的相对误差REq1和REq,从对比中可看出,辅助边值问题法比规则化边界积分方程的准确性稍好,这主要是因为辅助边值问题法计算系数矩阵的对角元可能更准确.
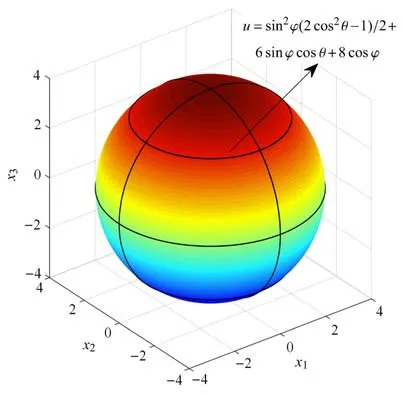
图4 单位球域Fig.4 Unit sphere
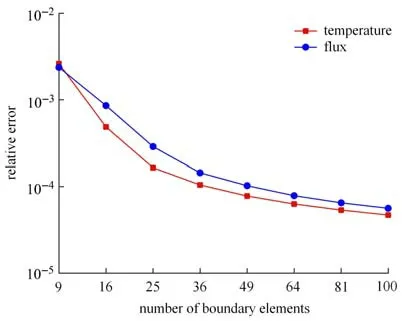
图5 场温度u 和通量q1=∂u/∂x1的收敛曲线Fig.5 Relative errors for the temperature and its derivative vs.the number of boundary element
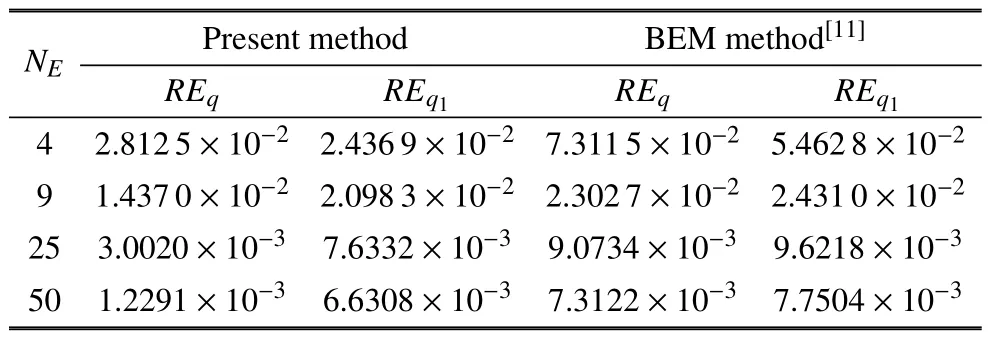
表1 不同单元数下,REq 和REq1的数值结果Table 1 The numerical results of REq and REq1with different boundary elements
算例3在最后一个算例中,考虑一个复杂区域上的热传导问题.计算区域是如图6 所示的一个变形长方体[31],它是由长方体{L×W×H=5.0 ×1.0×1.0}变形得到,其中L,W,H分别代表长方体的长、宽、高.变形长方体的上、下面的两条长边可分别表示为,左、右侧面的宽度和高度不变.在变形长方体边界上施加混合边界条件,其中变形长方体下面通量已知,其余各面温度已知,问题的解析解为u(x1,x2,x3)=x1x2x3+10x1+10x2+10x3.
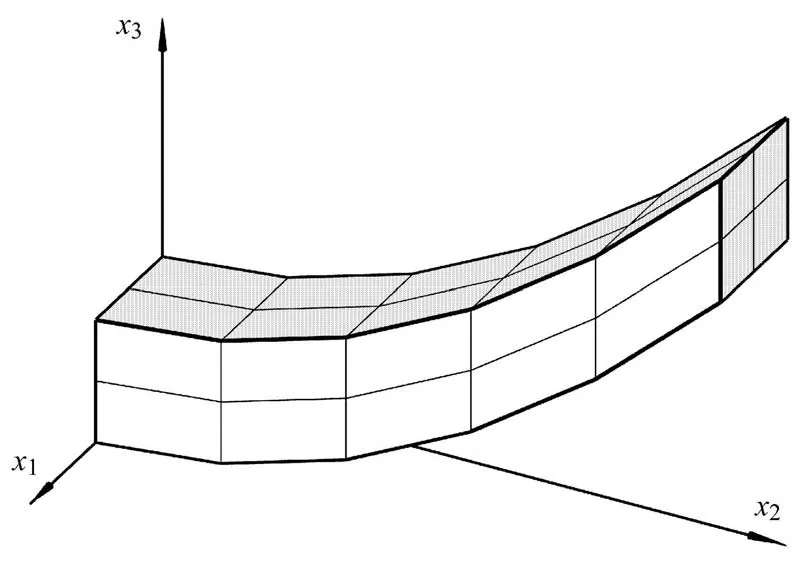
图6 变形长方体边界网格Fig.6 The boundary meshes of the deformed cuboid
采用混合单元计算.变形长方体的边界被划分为48 个单元,其中左、右侧面各划分为4 个线性单元(精确单元),其余4 个面各划分为10 个8 节点四边形2 次单元,如图5 所示.沿着变形长方体的中心线选取10 个计算点,表2 列出了10 个计算点上的温度u数值解以及精确解.此外,图7 给出了变形长方体的5 个表面(不包括下表面)上的边界节点处的法向梯度∂u/∂n和梯度∂u/∂x1的相对误差随边界单元数增大的变化情况,即收敛曲线.
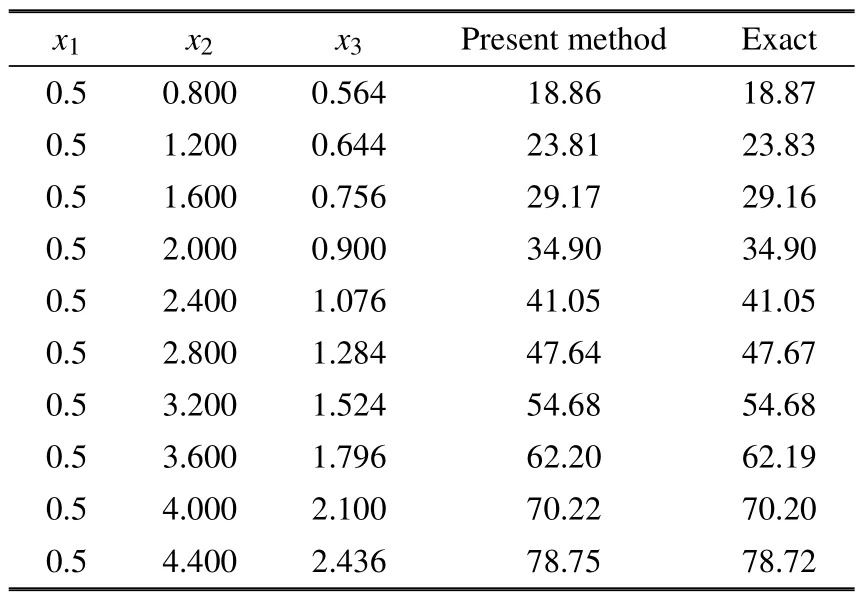
表2 沿着长方体中心线上的点的温度u 的数值结果Table 2 Numerical results of the temperature of a point along the center line of a cuboid
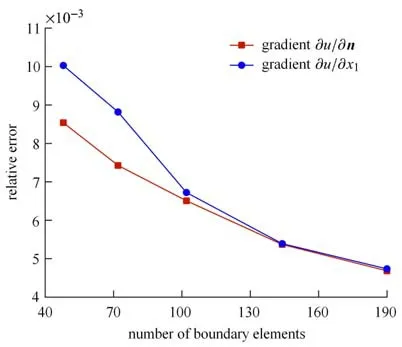
图7 边界法向梯度∂u/∂n 和梯度∂u/∂x1的收敛曲线Fig.7 Relative errors for the boundary quantities and derivative vs.the number of boundary elements
4 结论
本文提出求解位势梯度边界积分方程的辅助边值问题法.构造与边值问题具有相同解域的辅助边值问题,通过求解辅助边值问题,可准确地获得梯度边界积分方程的离散系统矩阵,计算过程不涉及强奇异边界积分的计算.所求得的系统矩阵可直接用来求解边值问题,不再需要重新计算系统矩阵.三个数值算例验证了方法的可行性、准确性及收敛性.此外,从与规则化边界元法的数值结果的对比可看出,本文方法的数值结果稍好一点,说明采用辅助边值问题法计算梯度边界积分方程的系统矩阵更准确,特别是对角元的计算.
本文为梯度边界积分方程的求解提供了新的思路.辅助边值问题方法具有理论简单,程序设计容易,精度高等优点,而且容易拓展到弹性问题、Stokes问题、Helmholtz问题等.

