借助二次函数图象 攻克函数参数求值问题

陈方圆

(江苏省南京市板桥中学 210039)

数形结合能够将函数的数量特征通过图象进行几何化，或者将函数某些几何特征转化为数量特征，将函数数量与几何特征紧密结合.二次函数作为试题中常遇到的函数，熟悉其图象和有关性质，可以搭建起求解有关二次函数的参数问题的便捷桥梁.

一、数形转化，实现参数问题直观化

二次函数是常见但极其重要的函数之一，许多参数问题都会或多或少地涉及到此函数.利用函数的性质思考函数的图象，借助函数图象思考对应的函数，在参数取值求解问题中，巧妙引入数形结合的思想，可以将问题形象直观地呈现出来，帮助问题又快又好地解决.如：

例1已知向量a=(x2,x+1)，b=(1-x,t)，若f(x)=a·b，且f(x)在区间(-1,1)时是增函数，求参数t的取值范围.

反思借助导数可以研究函数的单调性，借助二次函数的性质求出函数最值；在对二次函数图象和有关性质熟悉后，有时并不需要将二次函数图象呈现在解题过程中.

二、数形相配，简化参数问题求解

在求解参数问题中，会遇到一些方程或者不等式两边对应的图象非常容易作出来，可以将这些方程或不等式的图象在同一坐标中表示表示出来，借助研究函数图象的交点或者位置关系，以形助数，实现问题的直观化，如：

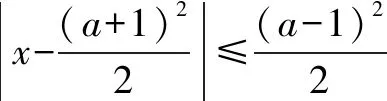
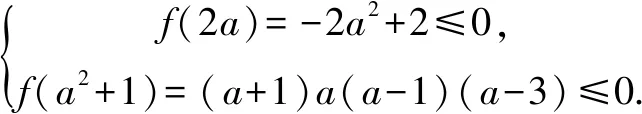
反思此题涉及到集合以及集合关系，需要将能表示的集合尽可能地表示；有关二次函数图象需要特别熟悉，掌握开口、对称轴、最值的求解方法，都将给画图或解题带来极大的便利.

三、数形结合，攻克参数取值问题

数形结合可以使得内容更加直观，从视觉上给解题带来一定的指引和帮助，再经过缜密的分析和逻辑思考，进而形成解题的完整思路.数形结合需要对函数解析式以及函数相对应的图形保持敏感性，敏捷灵活地将某类函数与图象进行等价转化，如对于非常熟悉的二次函数图象.熟练将二次函数图象进行表示，将极大简化求解步骤，如：

例3函数f(x)=x3-ax2+bx+5(a,b∈R)，若函数g(x)=f(x)-(b-1)x-5，且在区间[1,2]内g(x)是单调递增的函数，求参数a的取值范围.

综上所述，a的取值范围是a≤2.

反思二次函数是高中数学中极为重要的基础函数之一，掌握二次函数图象，熟练将图象进行呈现，以及灵活运用相关内容，是十分必要的；对二次函数问题中的分类要避免遗漏.

一般而言，高中数学中的函数问题都是基于常规函数进行演变和复合的，对于此类函数，要积极将导数知识进行关联，并借助数形结合思想，实现问题的直观化、简洁化，减少计算量，提高参数范围问题求解的正确率.