由一道模考题引发的思考与探究*

广东省江门市新会陈经纶中学

一道高三模拟试题,因为学生的疑问,引发了笔者的释疑、思考、探究和感悟,并因此体会到了作为教师“教学无止境”和“教学相长”的快乐.

一、问题的提出

在2019年江门市第一次模拟考试结束后,笔者在课上评讲了下面这道试题:

例1(2019年江门市第一次模拟考试第10题) 在直角坐标系xOy中,双曲线1(a,b ＞0)与抛物线y2=2bx相交于A,B两点,若ΔOAB是等边三角形,则双曲线的离心率e=( )

图1

教师给出的解法如图1,由题意设ΔOAB的边长为2m,则将A坐标分别代入两个曲线方程,得所以从而故选D.

课后,我班科代表眉头紧锁的来到办公室,问:“老师,您刚才讲的第10题,我有不同的想法,但解不出来,不知道怎么回事?”

学生的解法设A(xA,yA),B(xB,yB),不妨设yA ＞0,yB ＜0.联立方程

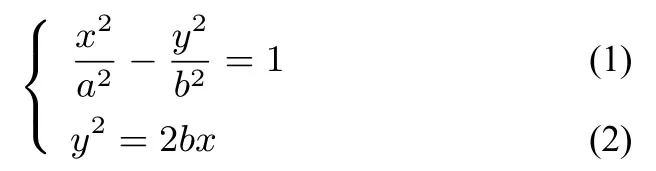
消y得:

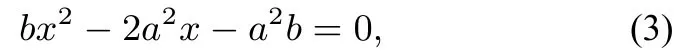
两种方法的答案不一致.我问:“你确定计算无误吗?”学生:“我和几个同学都算过好几遍了,应该没有错!”我检查了一遍学生的解法,确认计算没有问题,而且整个过程也合理.怎么回事呢?于是,我回忆了我做该题的思考过程: 按照经验,联立两个二次曲线的方程通常计算量大,所以尽量回避,利用等边三角形的性质巧妙的设出点A坐标,代入两个方程得出a,b关系,进而得到e.事实上,因为有直线与二次曲线相关问题的解题经验,科代表的想法才是更自然的想法,应该也代表了不少同学的真实想法.是这种方法行不通,还是中间环节出了问题?

二、问题的初步解决

为了解答学生的疑问,我们需要考虑如下两个问题:

问题1方程(3)一定有解吗?若有,有几个?

问题2真的是方程组的解吗?

首先考虑问题1.由于Δ=4a4+4a2b2＞0,所以(3)有两个互异根,不是xA=xB.

这样能得到正确结果!因此,可以断定,问题出在联立方程(1)(2) 得方程(3),利用韦达定理求xA上.究其原因是方程(1)(2) 转化方程(3) 的过程中并不等价,例如: 由仍然能得到方程(3),所以方程(3)的根不一定是方程(1)(2)的根,也即是出现了增根的情况,导致之后用韦达定理得到错误的xA.分析到这里,学生略带兴奋地说:“原来是这样!以后遇到两个二次曲线相关问题时,我可不敢联立方程去做了.”我说:“你只是说对一半,不是不敢,只是要慎重!”学生心满意足地走了,紧皱的眉头早已舒展开了.

三、问题的进一步探究

学生离开后,我却陷入了沉思,为什么会出现问题1和问题2的奇怪现象呢?应该怎么解决?笔者通过一番思考探索,得到了一些粗浅的认识.

回到问题1,我们自然会想:为什么利用判别式可以判定直线与二次曲线的位置关系,而对于两条二次曲线却失效了呢?原因是由方程组消y得到关于x的一元二次方程,利用判别式Δ＞0 只能说明x有解,而不能确保y有解.因此,在保证x有解的前提下,让y也有解就可以了.从函数的观点来看,为了使方程在某个范围内有解,就是要对应的函数在该区间有零点.基于上述分析,我们用判别式结合零点分布来解决两条二次曲线的位置关系问题,不妨称之为“判别式+零点分布法”,下面举例说明.

例2抛物线x2=2y与椭圆x2+4(y-a)2=4 有公共点,求a的取值范围.

解联立方程消去x,得:

令f(y)=2y2+(1-4a)y+2a2-2.在方程x2=2y中,y ≥0,要使抛物线x2=2y与椭圆x2+4(y-a)2=4 有公共点,方程(*) 需满足:一根在[0,+∞),另一根在(-∞,0)或两根都在[0,+∞).所以,f(0)≤0或解得:-1≤a ≤1或故a的取值范围为:

借助上面的“判别式+零点分布法”,我们从另外一个角度看问题2 出现增根的原因:

联立(1)(2) 消去x得:

令t=y2(t ≥0),则方程(4) 化为t2-4a2t-4a2b2=0.设该方程的解为t1,t2(t1＜t2).

又令f(t) =t2-4a2t-4a2b2,则f(t) 在[0,+∞) 有解,显然Δ＞0,f(0) =-4a2b2＜0,故所显然不符合).

以上是解决两条二次曲线的交点问题的一种思路,有没有更简便的方法呢?下面尝试利用圆锥曲线的参数方程来处理问题,称之为“参数法”.

例3(例2的另解) 椭圆x2+4(y-a)2=4的参数方程为代入抛物线方程x2=2y得:4 cos2θ=2(a+sinθ),所以

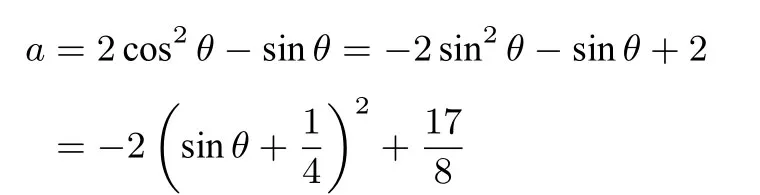
因为θ ∈[0,2π),所以所以

例4分别求圆的半径r的取值范围,使椭圆x2+4y2=4与圆(x-1)2+y2=r2分别无公共点,有1个,2个,3个,4个公共点.

解椭圆x2+4y2=4的参数方程为代入圆方程得:

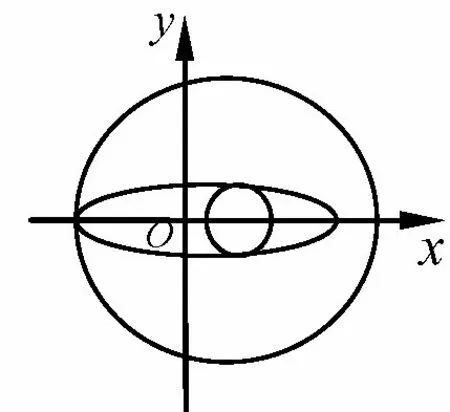
图2

r2=(2 cosθ-1)2+sin2θ=3 cos2θ-4 cosθ+2 =3因为θ ∈[0,2π) 所以cosθ ∈[-1,1],从而即当时,椭圆与圆有公共点.结合图2可知,当r取最值时椭圆与圆相切.故当或r ＞3时,无公共点;当r=3时,有1个公共点;当或1＜r ＜3时,有2个公共点,当r=1时,有3个公共点;当时,有4个公共点.

四、感悟

教师通常有较多的解题经验,容易找到解题的正确道路或更优的方法.但是,对学生来说,有一些“自然的想法”,不一定很完善,有时甚至会很麻烦,而且部分学生喜欢“打破沙锅问到底”.对此,教师不能回避或简单否定,应该予以因势利导,答疑解惑,反之,不仅会打击学生的“勇于探究”的积极性,还可能错过了发现新问题新方法的机会,培养学生的核心素养也就无从谈起.在本次教学经历中,正是由学生这种“追根求源”的精神激发了笔者地思考探索,从而加深了对两条二次曲线位置关系问题的理解,如果说学生在这个过程中得到了成长,于我又何尝不是呢?真所谓“教学相长”也!