合力与两分力夹角的函数图像研究

熊安丽

(上海市奉贤中学,上海 201499)

1 问题

在高一力的合成教学中,发现这样一类问题,即给出两个大小不变的共点力的合力F随两分力夹角θ的变化曲线,要求出两分力的大小分别为多少．这时会出现有的题目解出的分力情况完全相同,但所配的F-θ曲线却截然不同,例如图1和图2,两分力的解均为一个力4 N、一个力3 N．

虽然图线形状对求解没有什么影响,但物理是一门科学严谨、探索求真的学科,F-θ的函数图像到底是什么形状、有何规律,笔者决定一探究竟．[1]

图1 配图实例1

图3 F1、F2合力的示意图

2 探究

2.1 F-θ的函数关系

设任意两个共点分力的大小为F1、F2,两分力的夹角为θ,则由平行四边形定则及几何知识易求得其合力F的大小与夹角θ的函数关系为

(1)

2.2 两分力4 N、3 N的F-θ的曲线

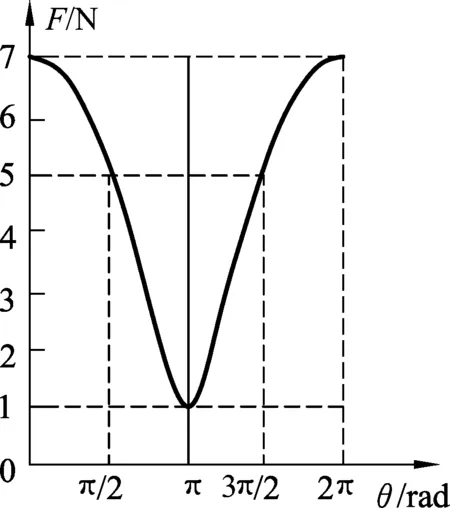
图4 两分力4 N、3 N的F-θ曲线

由图可看出:两分力4 N、3 N的合力F-θ曲线的特点是,当θ=π/2或3π/2时,曲线并不与该点处的竖直辅助线相切,所以图1错误.另当θ=π时,曲线与该点处的水平辅助线相切,呈现平滑的下凹型,并不如图2那般有明显地向下尖端,因此图2也错误．那么,是否所有的F-θ曲线都是图4这般模样,不同分力的F-θ曲线会不会有所不同?笔者决定进一步研究．

2.3 F-θ曲线的其它实例

为便于对比,接下来的实例笔者选取的是研究“同向相加后合力均为7 N”的两分力的合力F-θ曲线,用几何画板或EXCEL软件均可依次作出两分力大小分别为“6.5 N、0.5 N”、“6 N、1 N”、“5.5 N、1.5 N”、“5 N、2 N”、“4.5 N、3.5 N”、“4 N、3 N”和“3.5 N、3.5 N”的F-θ曲线(如图5),可发现曲线具有一定的规律性:即当θ=0时,合力始终最大,为F1+F2;在θ∈(0,π)范围内,合力F都是随两分力夹角θ的增大而减小;当θ=π时,合力始终对应最小,为|F1-F2|;在θ∈(π,2π)范围内,合力F也都是随两分力夹角θ的增大而对称地增大;当θ=2π时,合力又都达最大值F1+F2,符合预期的判断．[3]另有新的发现,即在两力之和一定的情况下,两分力大小相差得越大,曲线越平缓;两分力大小越相接近,曲线则越陡峭,下凹明显且下凹处逐渐变得尖锐．

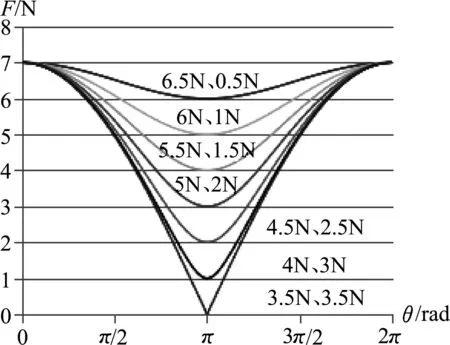
图5 F-θ曲线其它实例

图6 各曲线的拐点位置及该点切线

并且F-θ曲线的弯曲程度即斜率也呈一定的规律性,考虑到曲线的对称性,现仅讨论θ∈[0,π]范围内的曲线规律,易发现F-θ曲线(除两分力相等的那条之外)在[0,π]的范围内均随θ的增大先逐渐下弯并越来越陡,后又会逐渐平缓,直至趋于水平．各条曲线上是否有斜率的极大值点,会有多少个极大值点,可借助几何画板或EXCEL软件进一步研究．用几何画板可直接右键点击F-θ函数,选择“导数”,得出F′-θ函数关系式并作F′-θ图,找出(0,π)范围内F′(θ)的负的极大值位置,但由于笔者所用几何画板版本的问题,它无法直接显示点的坐标,而人工估读误差较大,所以笔者主要利用EXCEL软件列表计算F-θ曲线上各点的斜率值F′(θ)来研究,并且发现在θ∈(0,π)的范围内,F′(θ)均为负值且每条F-θ曲线的F′(θ)值仅有一个负的极值点,找出其所对应的θ角,即可确定每条F-θ曲线上的斜率最大值点的大致位置并作出该点切线(如图6),在[0,2π]范围内的F-θ曲线斜率的特点可归纳为表1.

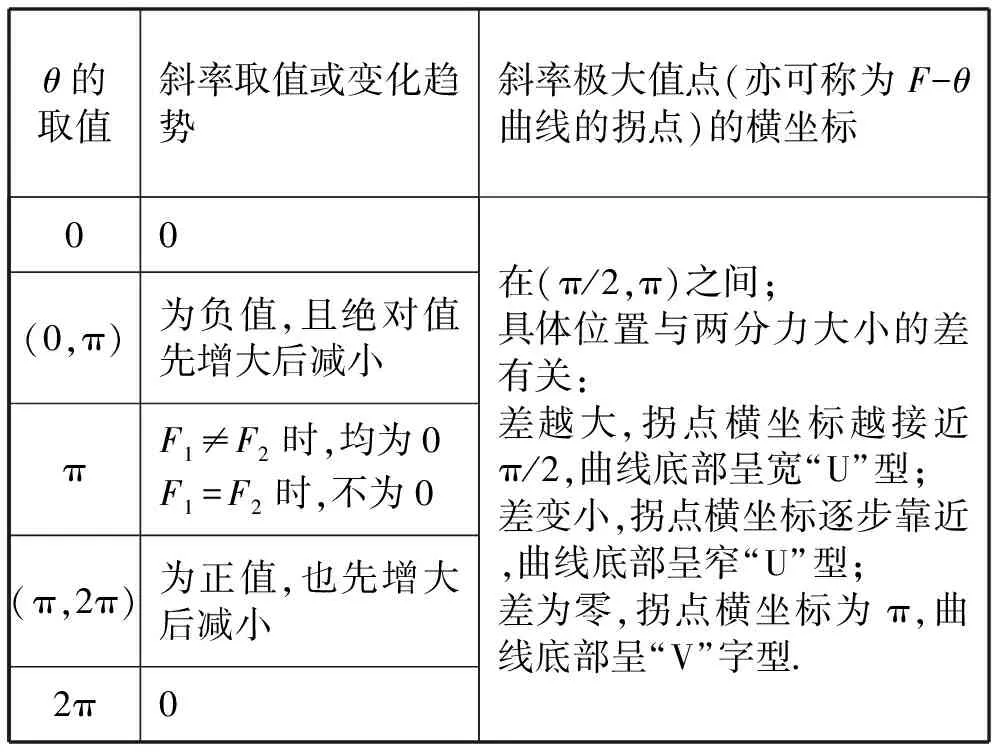
表1 F-θ曲线斜率的特点

上述结论具有一定的指导意义,对于任意两个力的F-θ曲线该如何画,特别是如何弯曲,可参照图5中某条适当的曲线对F轴进行一定比例的压缩或拉伸而得．但是,这个结论又不够具有普适性,因为EXCEL表格中θ角取值的有限性,以及应用π计算时取值的精确性,都导致拐点的位置无法准确确定,且每对应一条任意大小的两分力的F-θ曲线,均需要列出大量数据表格才能大致找出拐点,非常繁琐而困难,因此笔者尝试在更具有普遍意义的函数通项式上研究．

2.4 F-θ曲线的理论研究

为方便研究,设任意大小的两分力F1、F2,且F1≥F2>0,其F-θ的函数关系及大小变化趋势不再赘述,接下来

(1) 研究F-θ曲线的斜率,可对其求导,得

(2)

(2) 研究斜率的变化规律和拐点位置,可对F′(θ)函数再求导并化简,得

(3)

图7 y关于x的函数曲线

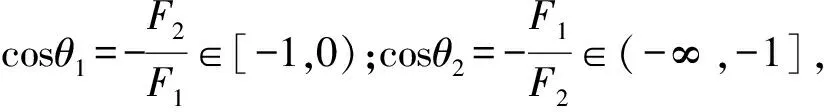
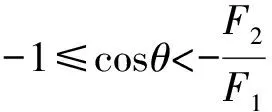
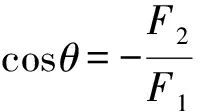
图8 F-θ斜率最大时，力的合成矢量三角形

3 归纳

根据以上的理论推导,可得出F-θ曲线的一些规律,即任意大小的两个分力F1、F2,若F1≥F2>0,则其合力F-θ曲线在[0,π]范围内应经过4个特殊状态点,各状态点所对应的分力夹角θ值、合力F值、曲线斜率F′(θ)的情况.

① 两分力同向.θ=0,F=F1+F2,F′=0.

易见,曲线在①、③点之间为上凸,③、④点之间为下凹．拐点③的位置随F1、F2的取值不同而在(π/2,π]区间内移动,F2的值相对F1越小,拐点角θ拐就越小,可无限逼近π/2;F2与F1大小越接近,θ拐越大,当F1=F2时,拐点角最大,为π．即拐点③在②、④两个点之间,③点只能逼近②点而不能与②点重合,因为要与②点重合就要F2=0,而讨论F2=0时的合力没什么意义,因为合力始终为F1;但③点可以与④点重合,即当两分力的大小相等时,此时曲线没有下凹段,在θ=π附近呈现“V”字型．

4 应用

应用上述总结的规律,可以验证2.3中所举的实例．首先,各曲线的凹凸趋势完全符合理论分析,下面着重说明[0,π]范围内应用理论计算各拐点坐标的方法,并与图6中各拐点的坐标作对比(如表2).

仔细观察并对比拐点坐标的EXCEL计算值和理论计算值,会发现几乎全部都一致,但是有一些误差,这主要是因为EXCEL作图需列出数据表格,再建立函数进行计算．在列出分力夹角θ项时,本人只精细到每隔1°=(1°/180°)×3.141592654rad取一个点,因此取点不够密集,在寻找斜率负极大值点时导致不够精确,而且在计算时应用到π值进行角度换算时,本人取的是π=3.141592654,也导致了数据的不完全精密,特别是在两分力相等时,EXCEL取点不能无限地逼近θ=π,导致拐点的位置确定和斜率计算误差相对较大．总之,用EXCEL软件来研究拐点的位置是比较麻烦而难以精确的,但是用理论推导则方便、精确得多．另外,F-θ曲线在[π,2π]范围内的拐点坐标可利用函数图像的对称性直接求出:θ拐′=2π-θ拐=π+arccos(F2/F1),此拐点的纵坐标与[0,π]范围内的拐点的纵坐标相等,非常容易和快捷．

表2 F-θ曲线拐点坐标的理论检验

目前许多参考书及题库网站上涉及到这类问题时所配的F-θ图像都是明显错误的,望笔者的研究能为各位同行和同学提供一点帮助．