基于锦标赛思想的最优计算量分配的研究

奚钰佳

摘要：序优化（Ordinal Optimization，OO）方法在随机仿真优化（Stochastic Simulation Optimization）中有较为流行。该方法提出了序（Order）比值（Value）更容易获得的思想，并提供了理论依据。而最优计算量分配（Optimal Computing Budget Allocation，OCBA）算法则是为了进一步提高序优化的效率提出的。该文主要针对最优计算量分配算法进行拓展。在数据和选择爆发式增长的情况下，在获得最佳选择（方案）的同时，也有必要缩短选择时间。锦标赛思想则是在有大量参赛选手时，两两比较选出优胜选手，再从优胜选手中进行选择，从而减少比较的时间。受此思想启发，面对大规模候选集，提出了基于锦标赛思想的最优计算量分配算法。该算法在对方案进行仿真资源的分配前，先选择一半甚至更少的精英方案，以快速的获得最佳方案。并且实验数据表明了其有效性。

关键词：随机仿真;序优化;最优计算量分配;排序和选择

中图分类号：TP311.1 文献标识码：A

文章编号：1009-3044（2020）05-0253-05

开放科学（资源服务）标识码（OSID）：

1 序优化方法介绍

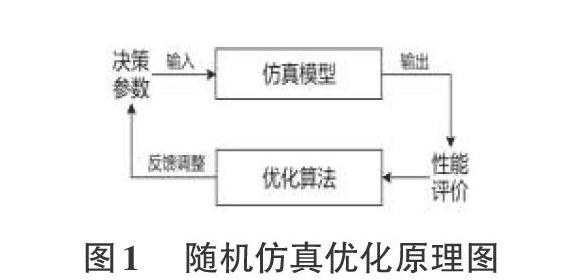
序优化方法（Ordinal Optimization，00）在随机仿真优化中有着较多的应用[1-2]。随机仿真优化即是基于仿真的目标优化，并且在很多实际系统中都有着广泛的应用[3][4]，比如复杂工程系统的设计优化、供应链和物流系统、制造系统及社会经济系统[[5-9]等。该方法将问题建模，通过优化算法根据仿真模型的输出对输入调整优化，从而选出性能最佳的对象。具体过程如图1所示：

在其中，有一类排序与选择（Ranking and Selection）问题，目标或者是要从候选方案（design）中获得最佳，或者是获得其方案的排序，抑或者是或者前m个最佳。对于这类问题，序优化思想有着更大的优势。其认为序（Order）比值（Value）更容易获得[10]，因此在仿真过程中，不必要对每个方案都大量仿真以獲得其精确值，根据目标，针对性的对方案进行分配，获得它们的序，从而更高效的达到目标。因此，序优化在应用到学习选择出最佳方案（子集）等问题时，具有巨大的优势，并被应用到了多个领域[11]-[13]。

Ho等人提出的序优化方法包含了两个主要思想：序比值更容易获得;不要坚持获得最佳（Best）的方案而要愿意接受足够好（Cood Enough）的方案[1][2]。该方法旨在从候选集中选出足够好（Good Enough）的方案，本来目标是选出真是最优，但是运用足够好（Good Enough）的思想，将选择范围拓宽到集合G，而s是仿真获得的足够好的集合，s中仿真估计最优也就会在集合G中，这也就达到了选择算法的目标：获得足够好的方案[1]。那么序优化的目标函数可以表示为：

其中AP意为Alignment Probability，表示对齐概率，而P{AP}={IGn JsI≥m），m就表示了想要达到的对齐水平。具体计算过程和分配过程见文献[1]。

近年来，基于序优化思想，在排序和选择问题中，已经提出了各种算法。方差比方法[l4]，基于两阶段的方法㈣[15][16]，这两种方法均是根据仿真结果的样本方差为方案候选方案分配仿真采样次数。基于无差异区的方法[17]和它的几个变体[18][19]采用频率派的方法。基于无差异区的方法选择属于无差异区的候选方案，这些候选方案的仿真结果并没有比最佳方案明显差，然后将大部分资源分配给属于无差异区的候选项。在文献[20]和文献[21]中，Chen等人基于序优化提出了最优计算预算分配方法，该方法根据仿真结果的样本均值和方差计算分配给各候选方案的仿真采样次数。

本文在下一节介绍了最优计算量分配算法，第3节介绍了本文提出的算法，第4节是实验结果及分析，第5节对本文做了总结。

2 最优计算量分配算法的介绍

最优计算量分配是Chen提出的一种基于贝叶斯理论的序优化方法[20][21]。该算法基于序优化中“序比值更好获得”的思想，在给定仿真采样资源的前提下，根据仿真获得的候选方案（design）评价值，给不同候选方案分配不同的仿真采样次数，并且着重分配给易与目标混淆的候选方案，从而提高算法的效率[21]。此外，该算法还对目标函数进行了严格的数学推导，为各候选方案应该获得多少仿真采样提供了理论基础。

该算法有这样的假设，假设候选方案i的性能服从正态分布N（μi，σ2），且相互独立。此外，其期望和方差未知，可通过仿

之后，基于最初的最优计算量分配，发展出了很多变体。Fu等人提出了具有相关性的采样情况下的最优计算量分配算法[22]。Chen等人提出了一种应用于选择最佳方案子集的最优计算量分配算法，这种最优计算量分配算法可以从方案候选集中选择出最佳的m个方案[23]。之后Zhang等人又对选择最佳m各方案的最佳计算量分配算法进行了改进[24]。He等人提出了运用期望机会成本来选择最佳方案的最优计算量分配算法[25]。

其中有些是以最大化正确选择概率（Probability of CorrectSelection.PCS）为目标来进行计算量的分配，有些是以最小化期望机会成本（Expected Opportunity Cost，EOC）为目标来进行计算量的分配。本文主要是对基于正确选择概率的最优计算量分配算法进行拓展，因此下面介绍原始的最优计算量分配。

最初的OCBA分配的目标就是找到真实最佳方案广，可以表示为[21]

上式表明了各候选方案的方差和与最佳方案6性能差距决定了其获得仿真采样的次数。方差越大，与最佳方案6性能差距越小，获得的仿真资源越多，而当前最佳方案6获得的仿真资源最多。这也符合前面所说的资源集中于易混淆对象的思想。在分配过程中，主要运用了渐进最优的思想，逐步的最大化APCS。

3 基于锦标赛思想的最优计算量分配算法

原始OCBA以及其变体在序优化问题上性能较好，但是仔细比较发现，这些算法的候选方案个数都偏小，而在如今的生活中，数据规模早已是百万、千万级别，个人、企业面对的选择也更多了。在这种情况下，我们在考虑最好的选择的同时，也有必要缩短我们的选择时间。

而锦标赛选择[26]的思想是在有大量参赛选手时，两两比较选出优胜选手，再從优胜选手中进行选择，从而减少比较的时间。受此思想启发，面对大规模序优化问题，可以先选择一半甚至更少的精英方案，再对方案进行仿真采样分配。

基于这一现实需求，受锦标赛选择思想启发，本文在OCBA的基础上提出一个新的算法：先选择精英子集，再对子集进行最优计算量分配，目标同样是最大概率的选出最佳方案。

表1中是本文要用到的数学符号及其定义。

3.1 问题分析

本文的目标是在候选规模较大时，找到这样一种计算量分配方案，能快速选出最佳方案并且正确选择概率最大。假设和最优计算量分配一致，候选方案性能的期望方差未知。由中心极限定理可知，大量仿真采样可以获得期望的估计[21]。假设每个候选方案的输出相互独立，且候选方案i的输出服从N（μi，σ2），那么μi就表示了方案i的真实性能，在无信息先验分布的情况下，基于贝叶斯理论对μi进行后验参数估计[11]得到

受锦标赛思想启发，先选出精英子集，再从精英子集中进行分配会更高效，因为这相当于子集之外的候选方案都不考虑分配仿真采样次数。精英子集Ss是从k个候选方案中通过仿真采样均值比较得出的s.k个均值最小的方案集合，其中s为精英方案占总候选方案的比例，

Ss=[i前s-k个最小的μ]

顺序不是必须的，是前s·k个最小均值的方案即可。不失一般性，我们的正确选择事件就变为

APCS即为PCS的下界，也就是近似正确选择概率（Approxi-mate Probability of Correct Selection，APCS）。而近似正确选择概率可以非常容易快速的计算出来。数值实验表明，使用APCS仍然可以高效的选出最佳方案[20][21]。因此，本文选择使用APCS来估计PCS。那么目标函数从（3.4）变为

基于OCBA程序框架，根据该定理本章提出了先选择top-s再进行分配地算法，命名为OCBAss。在程序初始化阶段，就对k个方案分别进行n0次仿真采样，以获得方案性能的采样信息，之后每一次循环都根据之前的仿真结果先选出精英子集Ss，再使用定理来计算Ss中各方案的仿真采样次数，每次循环新增△次仿真采样，直到T用完。该算法过程如表2所示。

可以看到，随着仿真的进行，精英子集Ss中的方案和方案6都可能会发生变化，但是随着仿真采样次数T—∞，算法会收敛到最佳方案。精英子集Ss的选择会使得仿真过程加快，因为每次循环都只用对s·k个方案进行分配和仿真。

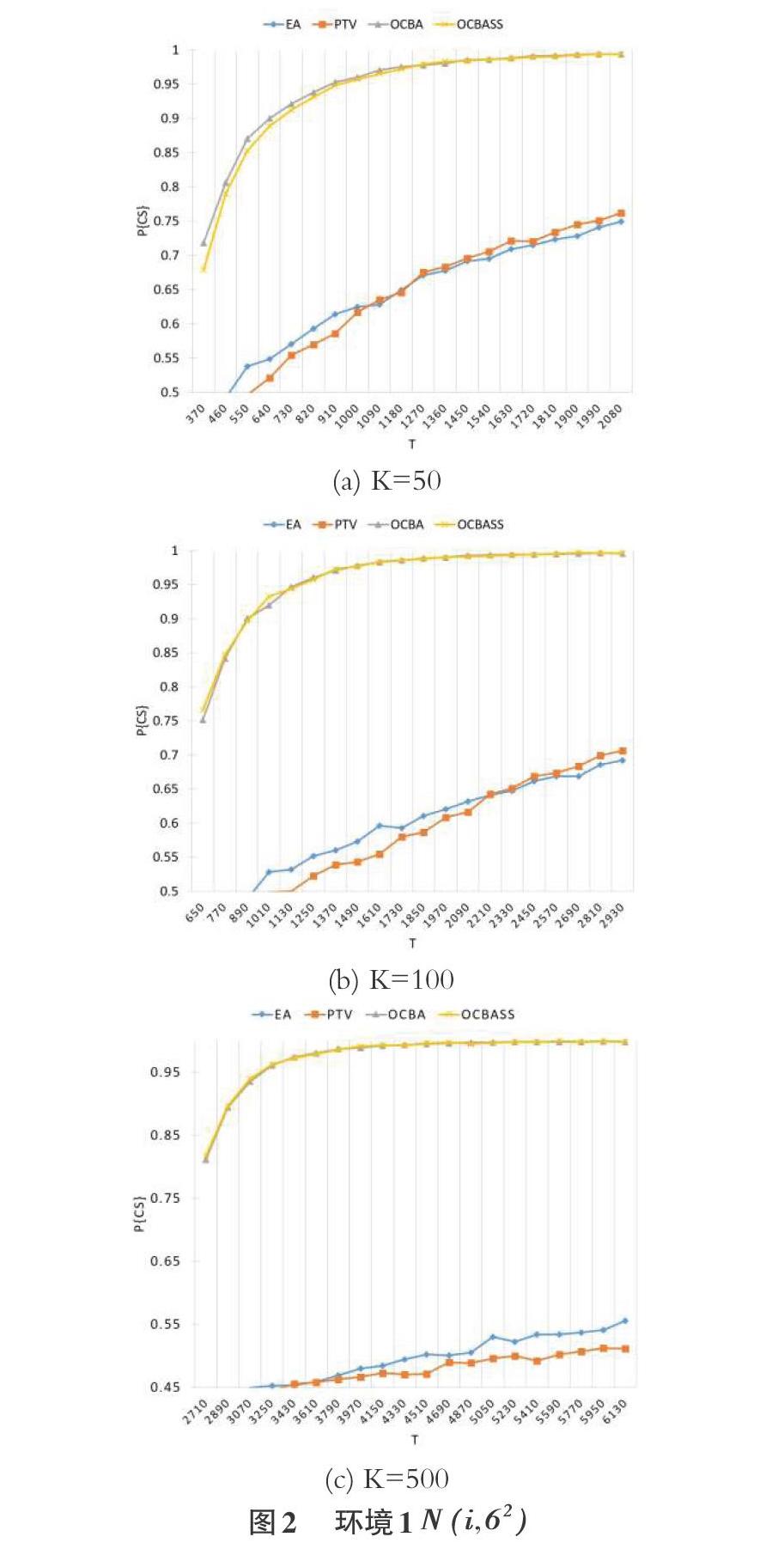
4 实验结果及分析选择概率P{CS}。环境1的实验结果见图2，环境2的实验结果见图3：

从图2的（a）（b）（c）可以看到，在环境1中，随着仿真资源T的增加，PCS也随之收敛，OCBAss的性能远高于EA和PTV，和OCBA也不相上下。从仿真时间这一角度进行比较，如下表3所示，可以发现，随着k的增加，OCBAss相对于OCBA节省的时间越多。

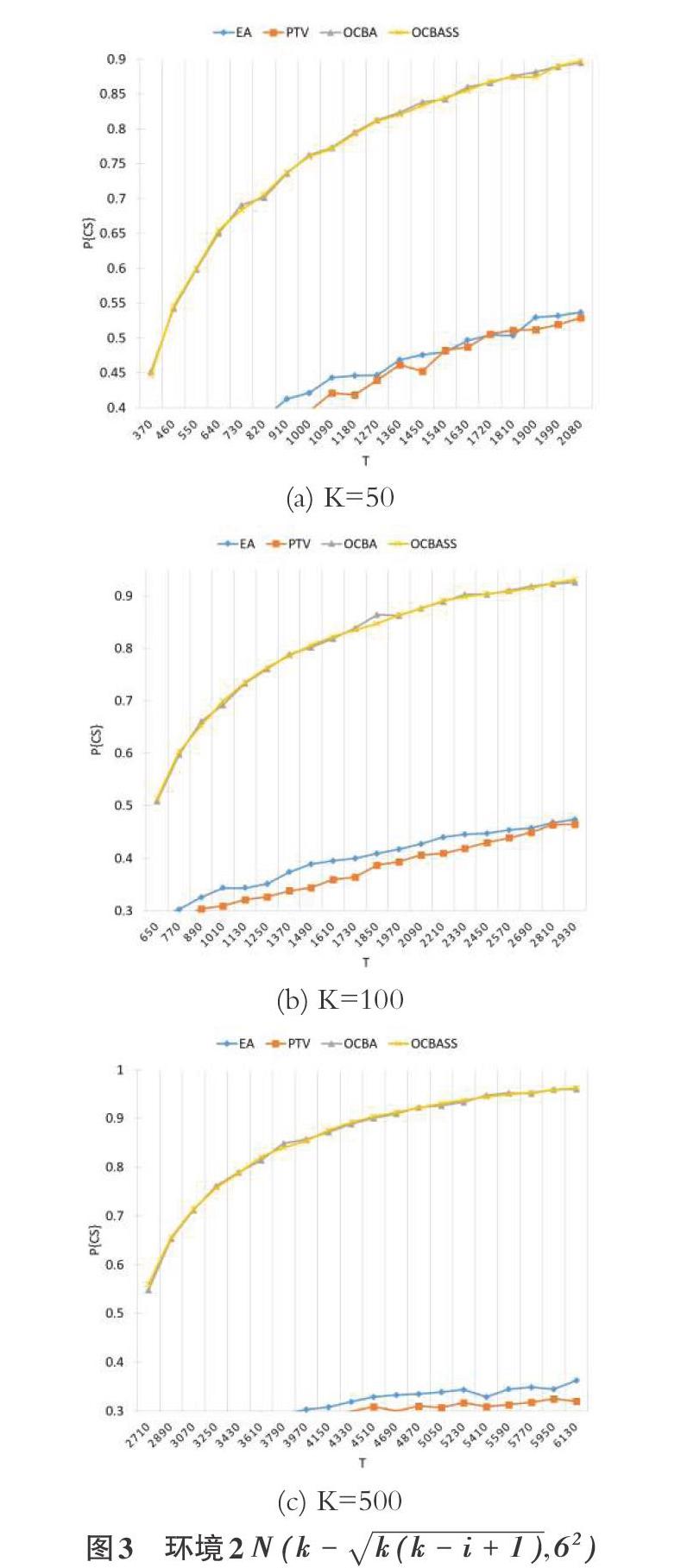
环境2各算法在不同规模下的收敛效果如图3所示，随着T的增加，PCS逐渐收敛，并且OCBAss远胜于EA和PTV，和OC-BA不分伯仲，同样优秀。而在仿真时间上，OCBAss优于OC-BA，可以更快速地得到同样的PCS，而随着k的增加，缩短的时间更多。可以预测，随着k增长到百万、千万，相比OCBA可以更快地达到预定的PCS。

综上所述，OCBAss在规模较大的环境下具有更高的优势。因为该算法增加了选择了精英子集的步骤，使得计算量大大减少。实验表明，尽管OCBAss策略简单，但是在候选方案规模较大时，不仅仿真时间缩短数倍，正确选择概率也和OCBA旗鼓相当。

5 结论

为了提升排序与选择算法对随机环境下大规模序优化问题的速度和精度，本文对序优化以及排序与选择进行了研究，受锦标赛选择思想启发，提出了针对大规模序优化问题的算法-OCBAss，并且本文在2个环境3种规模的实验中将其与EA，PTV，OCBA进行比较，结果表明了其优势。而这也表明了，在候选方案规模成千上万、上百万时，该算法缩短的时间更多，而精度不减。今后，也可以将其应用到各个大规模的领域[3]一[9]。因此，在未来的工作中，对于排序选择问题，可以对序优化思想进行深入的研究与探索，深入分析关键参数与步骤，提出更为有效的分配过程的同时，寻求理论突破。

参考文献：

[1] Ho Y C，Sreenivas R S，Vakili P.Ordinal optimization ofDEDS[J]. Discrete event dynamic systems， 1992， 2（1）：61-88.

[2] Ho Y C.An ordinal optimization approach to optimal controlproblems[J]. Automatica， 1999， 35（2）：331-338.

[3] Gosavi， Abhijit. Simulation-Based Optimization： ParametricOptimization Techniques and Reinforcement Learning， 2nded.， New York， NY， USA： Springer， 2014： 1-35. vol. 55.

[4] Fu M C.Optimization for simulation： Theory vs. Practice[J].lNFORMS Journal on Computing， 2002， 14（3）：192-215.

[5] van RensburgJ J，He Y，Kleywegt A J.A computer simula-tion model of container movement by sea.Proceedings of theWinter Simulation Conference， 2005. lEEE， 2005：8 pp.

[6] Yun W Y，Choi Y S.A simulation model for container-termi-nal operation analysis using an object-oriented approach[J]. In-ternational Journal of Production Economics， 1999， 59（1-3）：221-230.

[7] Saanen Y A，Valkengoed M V.Comparison of three automatedstacking alternatives by means of simulation. Proceedings ofthe 37th conference on Winter simulation. Winter SimulationConference， 2005： 1567-1576.

[8] Lim A，Rodrigues B，Xu Z.A m-parallel crane schedulingproblem with a non-crossing constraint[J]. Naval Research Lo-gistics （NRL）， 2007， 54（2）：115-127.

[9] Yang C H，Choi Y S，Ha T Y.Simulation-based performanceevaluation of transport vehicles at automated container termi-nals[J]. OR spectrum， 2004， 26（2）：149-170.

[10] Chen C H，Wu S D，Dai L Ordinal comparison of heuristicalgorithms using stochastic optimization[J]. lEEE Transactionson Robotics and Automation， 1999， 15（1）：44-56.

[11] Chick S E.Bayesian analysis for simulation input and out- put. Winter Simulation Conference. 1997： 253-260.

[12] Law A M， Kelton W D，Kelton W D.Simulation modelingand analysis[M]. New York： McGraw-Hill， 2000.

[13] Chen C H.A lower bound for the correct subset-selectionprobability and its application to discrete-event system siruula-tions[J]. lEEE transactions on automatic control， 1996， 41（8）：1227-1231.

[14] Law， Averill M.， Simulation modeling and analysis， 4th ed[M]. New York， NY， USA： McGraw-Hill， 2007.

[15] Dudewicz E J， Dalal S R. Allocation of observations in rank-ing and selection with unequal variances[J]. Sankhya： The In-dian Journal of Statistics， Series B， 1975： 28-78.

[16] Rinott Y. On two-stage selection procedures and relatedprobability-inequalities[J]. Communications in Statistics-Theo-ry and methods， 1978， 7（8）：799-811.

[17] Kim S H， Nelson B L. Selecting the best system[J]. Hand-books in operations research and management science， 2006，13： 501-534.

[18] Hong L J， Nelson B L. The tradeoff between sampling andswitching： New sequential procedures for indifference-zone se-lection[J]. IIE Transactions， 2005， 37（7）：623-634.

[19] Tsai S C， Nelson B L. Fully sequential selection procedureswith control variates[J]. llE Transactions， 2009， 42（1）：71-82.

[20] Chen H C， Chen C H， Yucesan E. Computing efforts alloca-tion for ordinal optimization and discrete event simulation[J].IEEE Transactions on Automatic Control. 2000， 45（5）：960-964.

[21] Chen C H， Lin J， Yucesan E， et al. Simulation budget alloca-tion for further enhancing the efficiency of ordinal optimization[J]. Discrete Event Dynamic Systems， 2000， 10（3）：251-270.

[22] Fu M C， Hu J Q， Chen C H， et al. Simulation allocation fordetermining the best design in the presence of correlated sam-pling[J]. lNFORMS Journal on Computing， 2007， 19（1）：101-111.

[23] Chen C H， He D， Fu M， et al. Efficient simulation budget al-location for selecting an optimal subset[J]. lNFORMS Journalon Computing， 2008， 20（4）：579-595.

[24] Zhang S， Lee L H， Chew E P， et al. A simulation budget allo-cation procedure for enhancing the efficiency of optimal subsetselection[J]. lEEE Transactions on Automatic Control， 2015， 61（1）：62-75.

[25] He D， Chick S E， Chen C H. Opportunity cost and OCBA se-lection procedures in ordinal optimization for a fixed numberof alternative systems[J]. lEEE Transactions on Systems， Man，and Cybernetics， Part C （Applications and Reviews）， 2007， 37（5）：951-961.

[26]夏桂梅.基于錦标赛选择遗传算法的随机微粒群算法[J]计算机工程与应用， 2007， 43（4）：51-53.

[27] Bratley P， Fox B L， Schrage L E. A guide to simulation[M]. Springer Science & Business Media. 2011.

[28] Winston W L， Venkataramanan M， Goldberg J B. Introduc-tion to mathematical programming[M]. Duxbury; Pacific Grove，CA： Thomson/Brooks/Cole， 2003.