求解复对称线性系统的CRI变型迭代法

杨 凤

(温州大学数理与电子信息工程学院，浙江温州 325035)

本文考虑下列非奇异复对称线性系统

其中 W ,T ∈ Rn×n均为对称矩阵，i为虚数单位．这类线性系统广泛存在于科学计算和工程应用中，例如涡流问题[1]、光散射成像[2]、分子动力学和流体动力学[3]等问题．

对于问题（1），当 W ,T ∈ Rn×n，且其中一个矩阵是对称正定的，另一个矩阵是对称半正定时，前人已经提出了许多的迭代法．基于线性系统系数矩阵的 Hermite和斜 Hermite分裂，Bai等[4]提出了HSS（Hermitian and Skew-Hermitian Splitting）迭代法，此后基于此类的迭代法层出不穷．例如为了避免求解系数矩阵为斜Hermite线性方程组，Bai等[5]提出了修正的HSS迭代法；为了加快MHSS（Modified Hermitian and Skew-Hermitian Splitting）迭代法的收敛速度，Bai等[6]又提出了PMHSS（Preconditioned Modified Hermitian and Skew-Hermitian Splitting）迭代法；Wang等[7]提出了CRI（Combination Method of Real Part and Imaginary Part）迭代法，并证明了CRI迭代法迭代矩阵谱半径的上界比PMHSS迭代法迭代矩阵谱半径的上界更小．

1 CRI迭代法

2 CRI变型迭代法

CRI迭代法[7]的迭代格式如下：

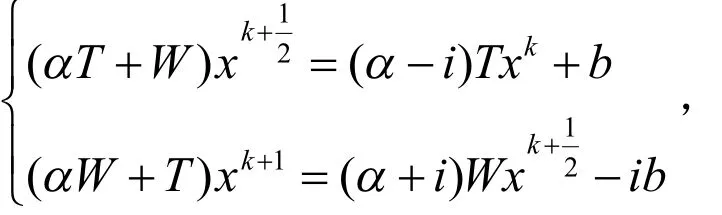
其中α为任意大于 0的实数．在复对称线性系统（1）的两边同时乘以(1 - i )有：由CRI迭代法迭代格式，得到了CRI变型迭代法的迭代格式

从而对∀α＞0，CRI变型迭代法对于线性系统（1）都无条件收敛．

证明：对CRI变型迭代法迭代矩阵做适当的变形有：

类似定理1的证明，设λ为矩阵φ(α)的特征值，由u表示T-1W的特征值知

当0＜α＜1时，h(α)单调递减；当α＞1时，h(α)单调递增．则α*=1时，h(α)取得极小值，将α*=1代入ρ(φ(α) ) 中，可得ρ(φ( 1 ))=，在定理 2的条件下，由推论 1知

3 数值实验

使用了一个复对称线性系统例子，通过CRI变型迭代法和CRI迭代法进行比较，验证了CRI变型迭代法求解复对称线性系统（1）的有效性和可行性．在实验中，分别从迭代次数（IT）、计算时间（CPU）、迭代误差（ERR）这三个角度进行比较，选择初始向量 x0为零向量，迭代误，其中 xk为当前的迭代残量．在CRI变型迭代法和CRI迭代法的比较中，令参数α=1．

例1 复对称不定线性系统（1.1）[5]的形式如下：

其中矩阵M和K是惯性和刚度矩阵，CV和τK是粘滞阻尼矩阵，ω是驾驶圆频率，τ是阻尼系数．

令 M = I,CV= 1 0I ，K是5点中心差分，在一个均匀网格上近似于具有齐次狄利克雷边界条件的负拉普拉斯算子的矩阵，而均匀网格[0,1]×[0,1]的尺寸大小矩阵K也是一个n阶块三对角矩阵，具有如下的张量积形式 ( n = m2)：

分别令ω =4,τ =1选择m=16, 32, 64, 128时，满足W是对称半正定矩阵，T是对称正定矩阵，以及本文的假设CRI变型和CRI这两种迭代法求解例1的实验结果见表1，表 1实验数据表明从迭代次数（IT），计算时间（CPU）和迭代误差（ERR）这三个角度来看，CRI变型迭代法都优于CRI迭代法，并且对于CRI变型迭代法求解的线性系统维数越大，迭代次数越小．

表1 例1的数值实验结果

4 结 论

本文分析了CRI迭代法收敛半径以及收敛半径的最优参数，在此基础上进一步提出了求解复对称线性系统的CRI变型迭代法，并给出了CRI变型迭代法的收敛分析以及最优收敛因子．在取最优参数的条件下，验证了在满足一定条件时，CRI变型迭代法比CRI迭代法的收敛半径更小，最后通过数值实验结果体现了此结论，并验证了CRI变型迭代法的优越性．