基于平均驻留时间切换离散线性系统的降阶输出反馈控制

何 伟,谢 巍,吴伟林,张浪文

(华南理工大学自动化科学与工程学院,广东广州 510640)

1 引言

近年来,线性矩阵不等式(linear matrix inequality,LMI)方法成了解决控制问题的有力工具.基于LMI的方法,一般可以构造出全阶的控制器.当被控对象的阶数较高时,全阶控制器由于实现成本高难以在工程中使用.阶数小于被控对象阶的降阶控制器设计问题是控制领域研究的基本问题.文献[1]研究了广义对象存在无穷远零点和单位圆上零点时的降阶控制器存在判据和设计准则.统一给出了混合H2/H∞控制问题的降阶控制器的设计方法.文献[2]考虑了线性时不变对象控制问题的降阶控制器的设计问题.同时给出了闭环控制系统性能的上界,该上界适用于标准和奇异控制两种情形.但是现有的降阶控制方法大多是关于连续系统的,而关于离散系统中的降阶方法并不多见.

研究者对离散时间切换系统的稳定性分析和控制器的设计越来越关注[3–5].由于其强大的工程背景,这类系统可在实践中得到更为广泛的应用[6–7].尽管目前有许多强大的线性分析工具,然而离散时间切换线性系统的稳定性和镇定问题仍然是一个具有挑战性的问题,因为即使在所有渐近稳定的子系统中,特定的切换信号下离散时间切换线性系统也可能变得不稳[8].对于自主切换,镇定问题可以看作是一个鲁棒控制问题,文献[9]提出了公共Lyapunov函数的存在是保证鲁棒稳定性的充分条件,然而,这种基于公共Lyapunov函数条件在特定的切换律下就会过于保守.因此,在具有受控切换的离散时间切换线性系统中,设计合理的切换律,达到闭环控制系统稳定和满足一定性能是很重要的.当考虑具有平均驻留时间(average dwell time,ADT)切换的离散线性切换系统的输出反馈控制时,切换系统的控制器的设计问题就会变得有些复杂.因为约束两个相邻Lyapunov函数跳跃的边界条件往往导致以双线性矩阵不等式(bilinear matrix inequalities,BMIs)的形式出现的非凸合成条件难以求解[10].文献[11]将边界条件纳入控制器的综合中,并使用控制器状态重置技术绕过了相关的BMIs的问题.

本文提出了一种具有ADT切换的离散线性切换系统输出反馈的降阶控制方法.该方法由一个切换动态输出反馈控制器,一个监控切换信号的监控器和在每个切换时刻执行切换控制器状态的复位规则组成(如图1所示).主要体现在其将边界条件的综合问题表述为凸优化的问题,从而可以得到关于ADT的全局最优解.此外,本文的方法不需要控制器状态重置的全部对象状态信息,这在很大程度上实现了降阶控制.最后通过一个算例结果来验证本方法的可行性.

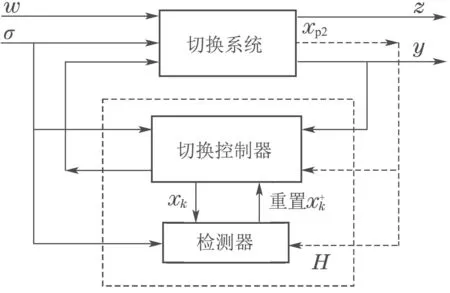
图1 混合控制框架Fig.1 The hybrid control scheme

2 定义和问题描述

考虑一个离散时间线性切换系统:

其中x(k)∈Rn,u(k)∈Ru和y(k)∈Rq分别表示系统的状态向量、控制输入、测量输出.

假定:A1)(Ap,i,Bu,i,Cy,i)对于i ∈I[1,Np]是可稳定的和可检测的;

A2)Dyu,i=0对于所有的i ∈I[1,Np]都成立.本文的设计目标:设计一个降阶控制律,使得切换系统(1)满足加权的l2增益性能的渐进稳定.

定义1对于切换信号δ和任何时间的间隔t2>t1>t0,假设Nδ(t1,t2)为切换信号δ在时间间隔[t1,t2]内的切换次数.如果对于条件N0≥1,τa>0,有Nδ(t1,t2)≤N0+(t2−t1)/τa始终成立,则称τa为平均驻留时间,N0称为颤动界.

引理1考虑一个切换线性系统(1).设0<λ0<1,γ >0和µ>1是给定常数,如果存在对称正定矩阵Pi,使得

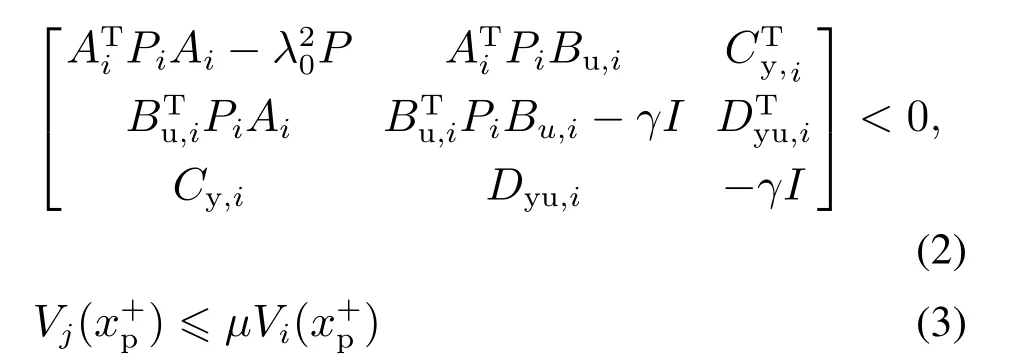
成立,那么切换线性系统(1)在平均驻留时间τa的切换信号下是全局一致渐近稳定(global uniformly asymptotically stable,GUAS)的，其中τa满足:对于任何正整数j >0,有

且在零初始条件下满足加权l2增益性能γ,即

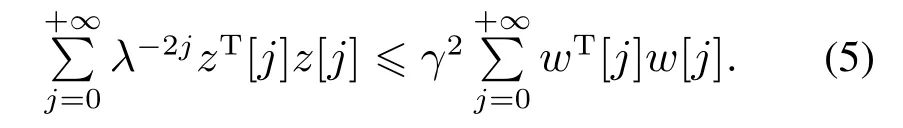
证 以上的结果很容易从定理2 的证明推导得到[12]. 证毕.

注1利用Schur补引理,根据文献[17–18],矩阵不等式(2)等价于以下条件:

i)存在对称正矩阵Pi,使得

ii)存在对称正矩阵Qi,使得

3 主要结果

3.1 降阶反馈控制律

考虑切换系统(1),其中部分状态测量是可用的.

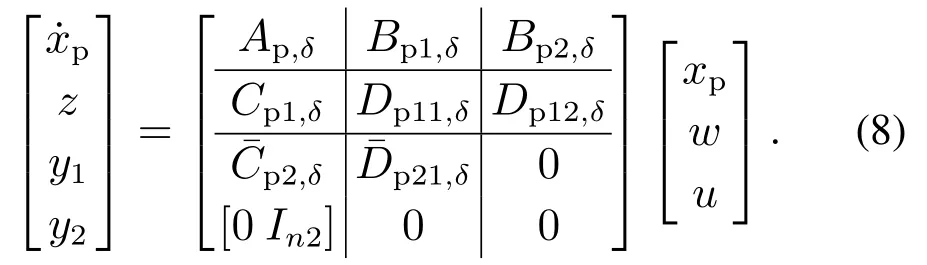
注意,测量的输出y:被划分为y1∈Rny1,y2∈Rn2和ny1+n2=ny.输出矩阵的特殊形式意味着最后的n2状态是可直接测量的,即让和xp1∈Rn1,xp2∈Rn2;然后,本文有y2=xp2和n1+n2=n作为结果,这样就可以构造n1–阶输出反馈律.

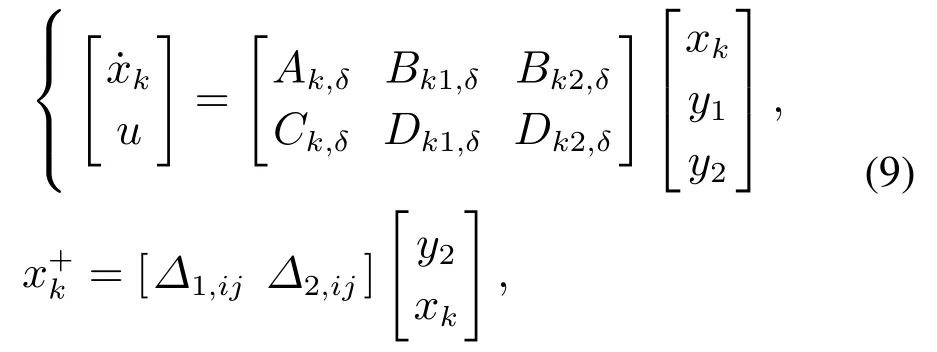
其中控制器状态xk ∈Rn1,∆1,ij ∈Rn1×n2和∆2,ij ∈Rn1×n1是重置矩阵.将式(9)的降阶控制器应用到式(8)的切换系统后,得到闭环系统的系数矩阵如下:

定理1考虑切换线性系统(1).给出两个可调标量λ0∈R+和µ>1,若存在正定矩阵和矩形矩阵.S2,i ∈Rn1×n2,Rn1×n2,对于所有的i,j ∈I[1,Np],i≠j.式(11)和(12)所求解的正标量γ ∈R+.然而,对于每个切换信号σ,在平均驻留时间τa≥ln(µ)/λ0内,具有GUAS的闭环系统(10),实现了加权l2增益性能γ.

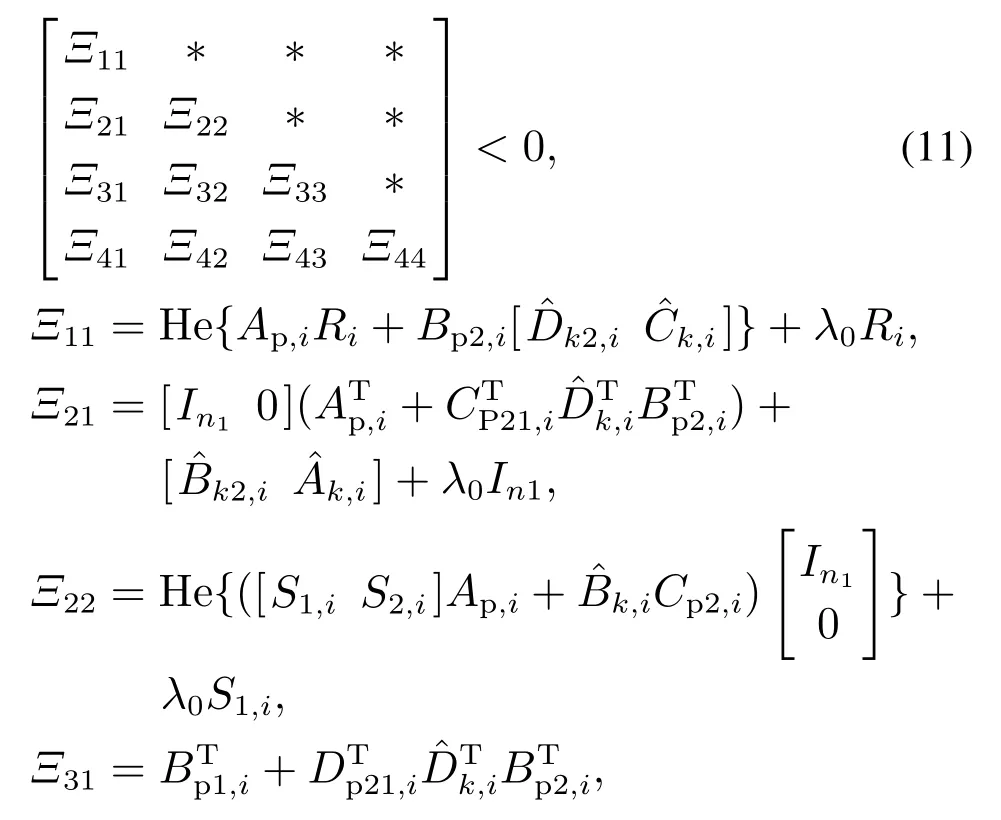
因此,通过以下算法可以得到降阶控制器系数矩阵:

1)分块矩阵

在R1,i,,对于所有的i ∈I[1,Np],本文有.注意,矩阵由引理2.1可得[16].

2)求解Ni ∈Rn×n1对于所有的i ∈I[1Np]通过因式分解,其中Qi ∈Rn1×n1,定义Mi=−RiNiQi,所以Mi,Ni满足独立的SiRi+.此外,本文还划分了Mi,Ni:Mi=,所以M1,i,N1,i ∈Rn1×n1是可逆的.并且M2,i,N2,i ∈Rn2×n1.

3)计算控制器系数矩阵Ak,i,Bk1,i,Bk2,i,Ck,i,Dk1,i,Dk2,i和∆1,ij,∆2,ij.对于所有的j ∈I[1Np]和i≠j,

其中

证为了保证GUAS稳定性和满足闭环系统(10)的加权l2增益性能,本文将相关的Lyapunov函数定义为在i ∈I[1,Np].

关于闭环系统状态中的xp1,xp2和xk的维数

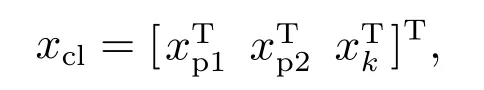
本文分解Lyapunov矩阵Pi:

并指定

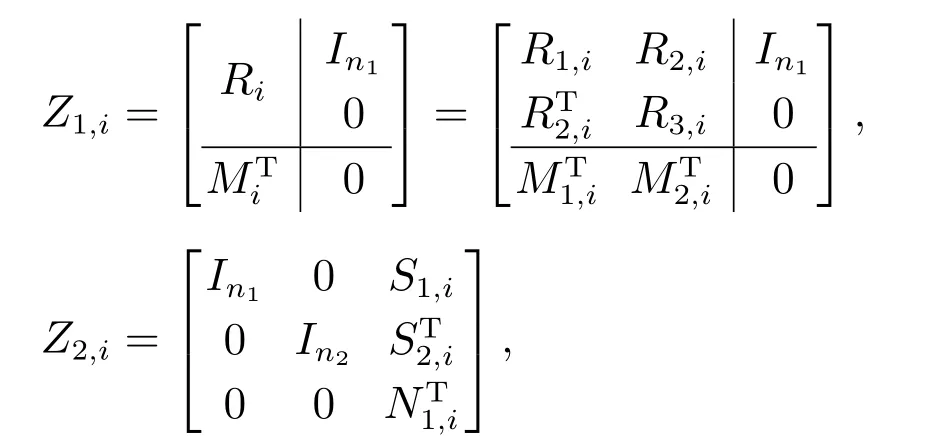
使PiZ1,i=Z2,i和.有

本文首先在条件(8)上进行同等变换,矩阵diag{Z1,i,Inw,Inz},并得到以下结果:

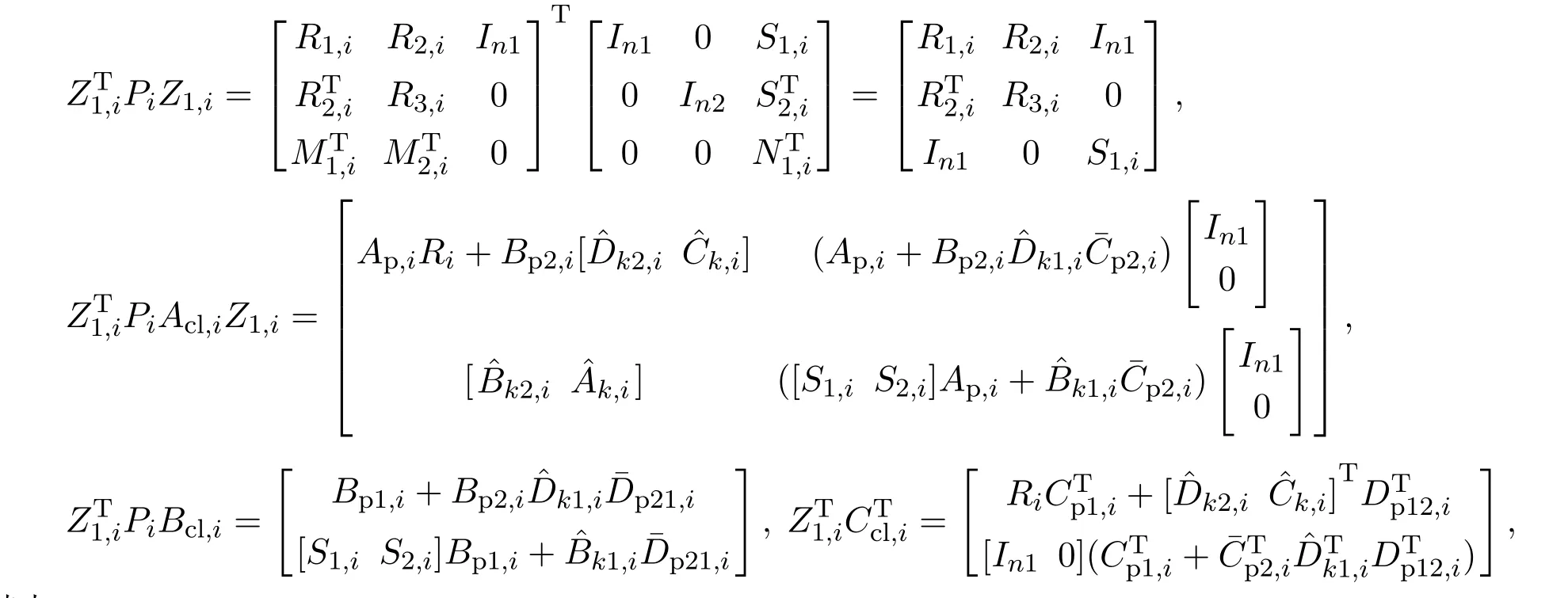
其中:

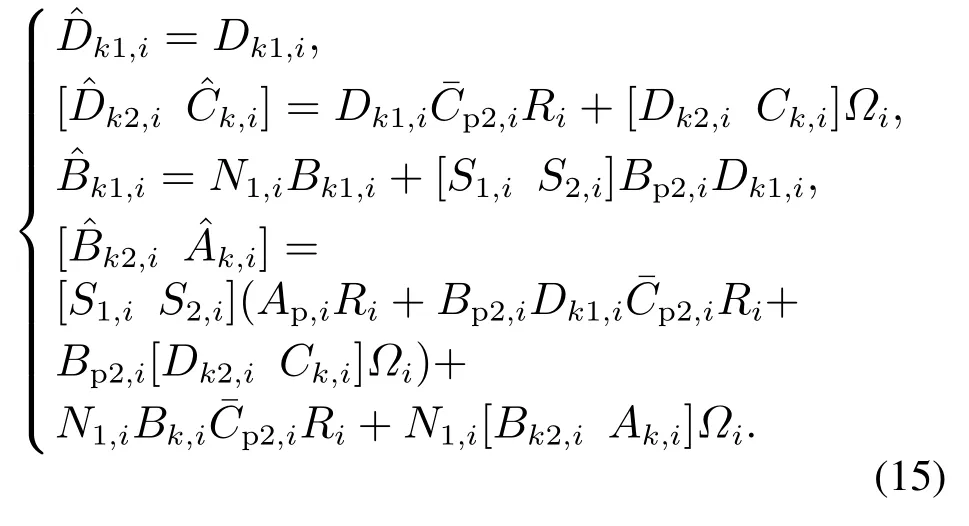
由于Z1,i是非奇异的,所以Lyapunov矩阵Pi >0可以由式(13)确定.另外,在同等变换后,式(11)还可以得到上述结果的条件.因此,通过执行矩阵diag{Z1,i,Z1,j}的同等变换得到了

其中

因此,式(12)可以通过LMI计算出来,式(14)所示控制器的系数矩阵也可以通过式(15)和式(16)反推导出来.

证毕.

根据定理1的结果,通过求解下列给定的LMI优化问题,可以确定降阶控制情况下最小加权l2的增益.(λ0,µ):

4 数值算例

本文给出的算例是文献[18]中的例子,通过采样周期T=0.5 s而得到的离散系统.考虑图2中的双罐系统.其中流体通过两个水槽,状态向量值选为两个水库水位值.假定流量的控制和水平面的测量能在两个水箱中任意切换.在没有控制的情形下,流入与流出的流体为常数且等于标称值.当输入与输出矩阵切换时,该系统的状态矩阵仍然没有明显的改变.本文选择如下的系统模型:

其中A中的矩阵是通过采样周期离散化得到;而输入和输出矩阵分别是

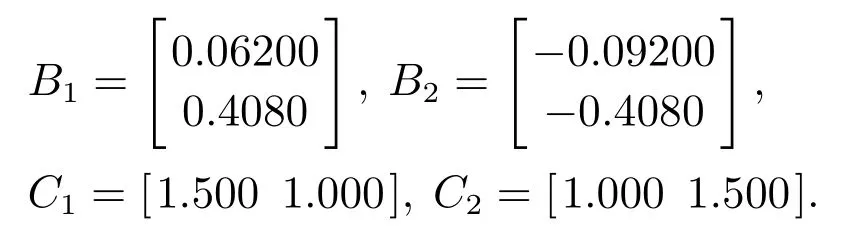
本文讨论了外部干扰抑制问题,其中选择加权函数为

通过求解式(17)的优化问题,本文得到了一个具有最优值γ=0.7625的降阶输出反馈控制器(9).

如图3所示,降阶控制反馈的受控输出响应具有很快的暂态过程和很好的静态特性.同时,在图4中,降阶控制输出反馈的控制力很小.

图3 系统的输出Fig.3 The controlled output

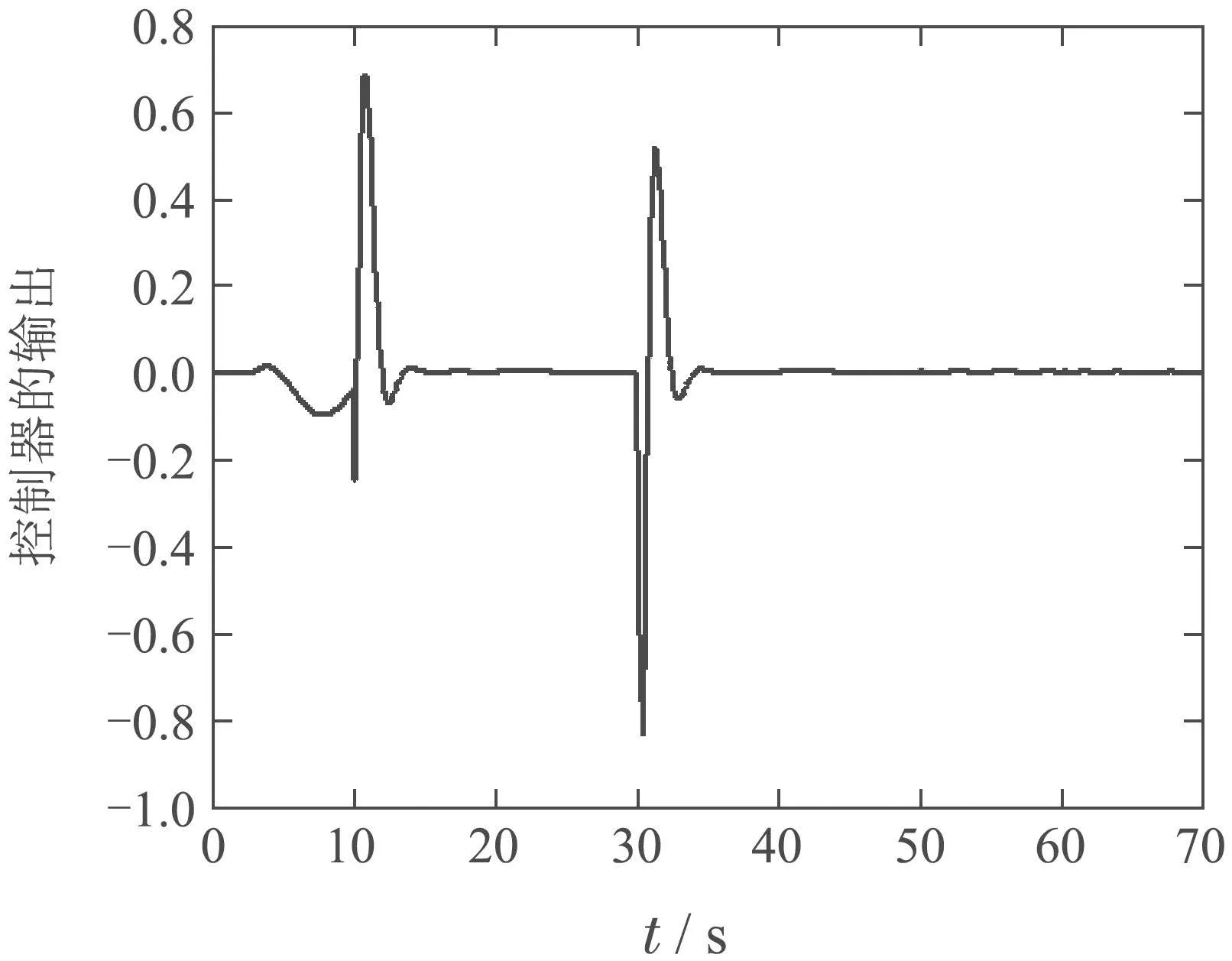
图4 控制器的输出Fig.4 The controller output

5 结论

针对具有平均驻留时间的切换离散时间线性控制系统,提出了一种降阶输出反馈控制方法.该方法将边界条件加入到综合控制问题中.利用多重二次Lyapunov函数,在统一的框架下,建立了具有保证稳定性和最优加权l2增益性能的降阶控制器.并将综合条件表述为一组具有给定的驻留时间参数的LMIs.为具有ADT切换的离散时间线性控制系统的综合提供了一种有效的、系统的方法.