应用Gauss-Bonnet定理研究Janis-Newman-Winicour虫洞的光线引力偏折

李宗海，周 霞，王 霞，李伟军，贺观圣

(1. 西南交通大学物理科学与技术学院，成都610031；2. 西华师范大学物理与空间科学学院，南充637009；3. 四川大学计算机学院，成都610065；4. 南华大学数理学院，衡阳421000)

1 引 言

引力透镜是引力理论的重要研究课题之一. 早在1921年，Eddington 及合作者[1]便借助于光线在太阳引力场中的偏折实验对爱因斯坦的广义相对论进行了验证. 目前，引力透镜在天文学与宇宙学中有极重要的应用，如探测黑洞、虫洞、引力单极子、暗物质和暗能量等[2-4].

引力透镜效应的传统研究方法是测地线法[5-7]. 该方法因其直观性被广泛应用于研究各种时空中的引力透镜效应. 这种方法不能展现引力偏折角的整体效应，且该方法的相关计算往往较繁琐. 最近，Gibbons 和 Werner[8]倡导了一种新几何方法 (GW法). 他们将 Gauss-Bonnet (GB) 定理应用于史瓦西时空对应的光学度规上，得到了计算引力偏折角的有效公式，并表明了引力偏折角是一种整体效应. 其后，Werner[9]将此方法推广到研究稳态时空中的引力透镜效应. Gibbons 和 Werner 所发展的这套方法既适用于广义相对论，也适用于其他引力理论[10-14]，这使得引力透镜效应的研究成果也层出不穷. 其中，Jusufi 及合作者[10-17]将该方法用于研究虫洞、宇宙弦等所致的光线引力偏折效应. Ishihara 及合作者[18-19]将 GW 法应用于研究有限距离情形下的光线引力偏折效应. Crisnejo 和 Gallo[20]将 GW 法推广至研究具有非零静质量粒子的引力偏折效应. 之后，Jusufi 及合作者[21-22]优化了文献[20]的方法，借助于引力透镜效应来区分裸奇点和黑洞及虫洞.

文献[11]指出，GW 法关于 JNW 虫洞中光线的二阶引力偏折的计算结果与测地线法的相应计算结果在二阶项上存在差异. 我们发现，这种差异源自作者对高斯曲率积分时采用了零阶光线轨道方程. 事实上，要正确计算光线的二阶引力偏折，必须考虑一阶引力效应对光线传播轨道的扰动. 本文以文献[11]的研究思想为基础，采用 GW 法将 JNW 虫洞引力场中的光线偏折效应计算至三阶. 本文也将证明，在史瓦西时空情形下，JNW 虫洞所致的三阶光线引力偏折角将简化成广义相对论中光线的三阶史瓦西偏折角，从而说明 GW 法与测地线法对引力偏折高阶贡献的计算结果仍然是一致的. 由于谐和规范能较大地简化计算[5]， 本文将在谐和坐标系中开展研究.

本文结构如下：第2节推导 JNW 虫洞的谐和规范解；第3节推导 JNW 虫洞谐和度规对应的光学度规，并计算其高斯曲率；第4节将 GB 定理应用到 JNW 光学度规上，得到计算偏折角的一般式，从而解析计算 JNW 虫洞所致的三阶光线引力偏折角；第5节对本文做出总结.

本文采用几何单位制G=c=1，并约定希腊字母值域为 {0,1,2,3}，拉丁字母值域为 {1,2,3}.

2 Janis-Newman-Winicour虫洞的谐和规范解

JNW虫洞在标准坐标系(t,R,θ,φ)中的线元为[11]:

(1)

其中，γ=M/m. M是ADM质量，m为一常数，两者与渐近标量电荷q的关系为M2=m2-kq2/2，其中 k(>0) 为物质-标量场耦合常数.

(2)

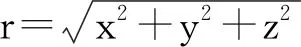
(3)

(4)

对于上式，一类方便的解为

R=c′r+m

(5)

其中c′为常数. 将方程(5)代入方程(3)，可得

(6)

令γ=1，方程(6)应为史瓦西时空线元. 对比文献[5]中的史瓦西谐和规范解，可知常数 c′=1. 因此，JNW虫洞的谐和规范解可表示为：

(7)

3 光学度规及其高斯曲率

由于JNW虫洞时空是球对称的，不失一般性，本文仅研究光线在其赤道面 (z=0) 内的引力偏折效应.令ds2=0，可得方程(7)对应的光学度规[8]：

(8)

(9)

(10)

(11)

(12)

将方程(10)～(12)代入(9)中，可得

(13)

4 Gauss-Bonnet定理和偏折角

设(D,gij)为二维紧、可定向微分流形. D⊂S，gij为D的黎曼度规，相应的高斯曲率为K. ∂D:{t}→D是D的边界，由分段光滑的曲线围成，其测地曲率为κ. 那么，Gauss-Bonnet定理可陈述为[8,11]：

(14)

其中，χ(D)为D的欧拉示性数，αi为曲线交点的外角，如图1所示.

区域D由分段光滑的曲线∂D1，∂D2，…,∂Dn围成，α1，α2，… ，αn为曲线交点的外角.

Fig.1 The diagram of the Gauss-Bonnet theorem

The domain D is formed by the piecewise smooth curves ∂D1, ∂D2, …, and ∂Dn, while α1, α2, …, and αnare the exterior angles of the intersections of these curves, respectively.

图2 Gauss-Bonnet 定理在透镜几何中的应用

S、O、L分别表示光源、观测者和引力透镜. L在区域DR0外，DR0由光线测地线γg和曲线CR0围成

Fig.2 The application of the Gauss-Bonnet theorem to the lensing geometry

S, O and L denote the light source, the observer, and the gravitational lens, respectively. L is located outside the domain DR0which is bounded by the light geodesic γgand the curve CR0

下面将GB定理应用于JNW虫洞的光学度规上. 如图2所示，考虑由光线轨道γg和一条曲线CR0：r=R0=constant围成的不包含引力源L的区域DR0. γg与CR0的交点分别为光源S和观测者O，其交点外角分别为αs和αo，α为光线引力偏折角. 因DR0不包含引力源L，有χ(DR0)=1. 又因光线轨道为测地线，故κ(γg)=0. 由于JNW光学几何是渐近欧几里得的，在弱极限近似下，若令R0→，则有αs+αo→π， κ(CR0)→1/R0和dt→R0dφ. 故GB定理可表示为：

(15)

即

α=-∬DKdS

(16)

方程(16)说明引力偏折角α是一种整体效应，其与坐标系的选择无关[8-9].

最后，考虑到方程(10)和(13)，可由方程(16)获得JNW虫洞赤道面内精确至3PM量级的光线引力偏折角：

(17)

其中，函数N的2PM解析式可由文献[7, 23]所倡导的后闵可夫斯基迭代技术来推导，结果如下所示：

(18)

方程(17)是本文的主要结果. 下面讨论该式的三种特殊情形：

(1) γ=2 时，对应q为复数的JNW虫洞. 在此情形下，方程(17)简化为：

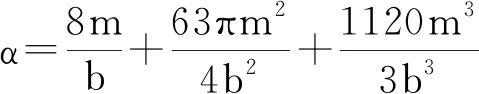
(19)

(2)γ=1/2 时，对应q为实数的JNW虫洞. 此时方程(17)简化为：

(20)

(3)γ=1 时，对应史瓦西时空. 此时方程(17)简化为：

(21)

根据上面的结果可知如下两点：第一，方程(17)右边的偏折角一阶贡献项与文献[11]的结果一致，而二阶项与文献[11]的结果存在差异. 这种差异来源于文献[11]在计算偏折角二阶贡献时忽略了一阶引力势对光线传播方程的扰动效应. 正是这种近似处理误导了作者，使其在该文献中做出GW法和测地线法对于引力透镜效应的计算仅在一阶偏折近似下一致的结论. 第二，由方程(21)可知，对于史瓦西时空这种特殊情形 (γ=1)，本文用GB定理所得到的三阶光线引力偏折角与测地线法的结果[24]完全一致. 这说明GW法与测地线法在计算高阶引力透镜效应时也是自恰的.

5 结 论

本文借助于Gauss-Bonnet定理计算了JNW虫洞赤道面光线的弱场引力偏折效应. 主要结论如下：(1) 获得了JNW虫洞引力场中光线的三阶偏折角. 其中，该偏折角的二阶贡献项和三阶贡献项的上述解析式均属于首次出现. (2) 本文的计算证明了GW法与测地线法在计算高阶 (如二阶和三阶) 引力偏折效应时也是自恰的. (3) 获得了JNW虫洞在谐和坐标系下的严格度规.