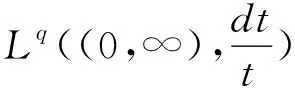Hölder’s Inequality for Generalized Orlicz-Lorentz Spaces
Xie Guangheng
(School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, China)
Abstract Let (Ω,μ) be a measure space. Assume φ:Ω×[0,∞)→[0,∞) is a Musielak-Orlicz function and q∈(1,∞). In this paper, we establish the Hölder inequality for the generalized Orlicz-Lorentz spaces Lφ,q(Ω). Especially, under the A∞ weighted condition, we show that the Hölder inequality holds true in weighted Lorentz spaces. Furthermore, the Hölder inequality for Orlicz-Lorentz spaces we obtained does not need any of those assumptions in Musielak-Orlicz setting. Only growth conditions are assumed.
Key words Musielak-Orlicz function Orlicz space Lorentz space Hölder inequality Weight Orlicz-Lorentz space
1 Introduction
Given a measure space (Ω,μ), we say thatφ:Ω×[0,∞)→[0,∞) is a Musielak-Orlicz function (also called generalized Orlicz function) if the following hold:
(i) for everyt∈[0,∞), the functionxφ(x,t) is measurable;
(ii) for everyx∈Ω, the functiontφ(x,t) is increasing;
(iii) limt→0+φ(x,t)=φ(x,0)=0 and limt→∞φ(x,t)=∞ for everyx∈Ω,
see [9] for more details. The generalized Orlicz spaceLφ(Ω) is defined in terms of the functional:
Generalized Orlicz spacesLφ(Ω), including classical Orlicz spaces as special cases have been studied since the 1940s. A major synthesis of functional analysis in these spaces, based on work, e.g. of Hudzik, Orlicz, and Musielak, is given in the standard reference standard reference in the field by Julian Musielak, which was published in 1983[18]. Recently, harmonic analysis in generalized Orlicz sapce has been studied. We refer to [20] for a detailed survey on the real-variable theory of generalized Orlicz Hardy spaces. In addition, a related field of research is partial differential equations with non-standard (Musielak-Orlicz) growth; see, for instance, [2] and the references therein.
The investigation of Lorentz spaces originated from Lorentz [16,17] in the early 1950’s. As a generalization of Lebesgue space, Lorentz spaces are known to be the intermediate spaces of Lebesgue spaces in the real interpolation sense. We refer the reader to Hunt [10], Cwikel [4] and Cwikel and Fefferman [5], and Jiao et al. [11,12] for a deep treatment of Lorentz spaces and their dual spaces as well as martingale Lorentz spaces.
It is well known that Hölder’s inequality is a very useful tool in analysis. Hölder’s inequality and the definition of the dual spaces of generalized Orlicz space can be found in [18] and also in [8]. For a detailed and complete survey of the recent progress related to the theory of generalized Orlicz spaces and its applications, we refer to the book [9]. On another hand, the Hölder-type inequalities in Lorentz spaces can can be proved easily, see Bennett and Sharpley [1]. Moreover, Kolyada and Soria in [15] studied optimal Hölder type inequalities for the Lorentz spaces. In this article, we consider the case of generalized Orlicz-Lorentz space which was first introduced in [13].
Letφbe a Musielak-Orlicz function andq∈[1,∞]. The generalized Orlicz-Lorentz spacesLφ,q(Ω) is defined to be the set of all measurable functionsfsuch that
is finite. This space is a generalization of many important Lorentz-type spaces including Lorentz-Zygmund space, Orlicz-Lorentz space, and weighted Lorentz spaces. Our main theorem presents a sufficient condition type inequality to hold in generalized Orlicz-Lorentz spaces.
Theorem 1.1Letφbe a Musielak-Orlicz function such that
(1.1)
and letq∈[1,∞]. If there exists a positive constantCsatisfying, for every measurable setA,
μ(A)≤Cφ(A)
(1.2)
and
(1.3)
then there exists a positive constantC1, depending only onφandq, such that
for allf∈Lφ,q(Ω) andg∈Lφ*,q′(Ω), whereφ*is the conjugate function ofφ(see Section 2 for its definition).
Now we turn to the weighted setting. To this end, we first introduce some notations. A weight is a non-negative locally integrable function onRnthat takes values in (0,∞) almost everywhere. Therefore, weights are allowed to be zero or infinite only on a set of Lebesgue measure zero.
Definition 1.2A weightωis called anA1weight, denoted byω∈A1, if there exists a positive constantCsuch that
Letp∈(1,∞). A weightωis said to be of classAp, denoted byω∈Ap, if
A weightωis said to be of classA∞ifω∈Apfor anyp∈[1,∞).
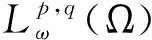
As a corollary of Theorem 1.1, we have the following weighted result.
Corollary 1.3Letω∈A∞,p∈[1,∞), andq∈[1,∞). If Ω⊂Rnis finite, then there exists a positive constantCsuch that

This paper is organized as follows. In Section 2, we first give the sufficient conditions for the Hölder inequality on generalized Orlicz-Lorentz spacesLφ,q(Ω), that is, we prove Theorem 1.1. We then show that these sufficient conditions are reasonable in some sense. Furthermore, we provide the proof of Corollary 1.3. Section 3 is devoted to establishing the Hölder inequality for Orlicz-Lorentz spaces.
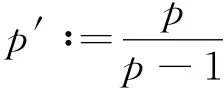
2 Proofs of Theorem 1 and Corollary 2
In this section, we prove the generalization of classical Hölder inequality related to the generalized Orlicz-Lorentz spaces. Firstly, we recall the notion of conjugate functions of Musielak-Orlicz functions. The Musielak-Orlicz functionφis said to be of uniformly lower typep(resp., upper typep) onAif there exists a positive constantCsuch that, for everyx∈Aandt∈(0,∞),
φ(x,st)≤Cspφ(x,t), ∀s∈(0,1) [resp., ∀s∈(1,∞)].
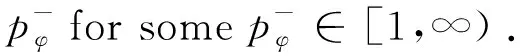
The Hölder inequality for Musielak-Orlicz function is the following
(2.1)
for allf∈Lφ(Ω) andg∈Lφ*(Ω). See, for instance, [9].
Remark 2.1Ifφis of uniformly lower (resp., upper) typep0onA, then, for everyp∈(0,p0) [resp.,p∈(p0,∞)],φis also of uniformly lower (resp., upper) typeponA. See [19] for more details.
Now we introduce the following notation, which is the generalization of the notation from the variable case [3]. For every measurable setA, let
and
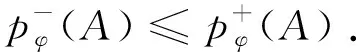
Lemma 2.2Letφbe a Musielak-Orlicz function. LetAandBbe two measurable sets. IfA⊂B, then
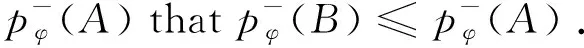

For every measurable setA, let
Now, we are ready to prove the main result of this paper.
Proof of Theorem 1.1For everyf∈Lφ,q(Ω) andn∈Z, let
rn∶=inf{λ∈(0,∞):φ({x∈Ω:|f(x)|>λ})≤2n}.
Clearly, the sequence (rn)n∈Zis non-increasing. Moreover, sincef∈Lφ,q(Ω), it follows that
Thus, we have
For everyn∈Z, let
An∶={x∈Ω:|f(x)|>rn}.
Now we claim that
(2.2)
and
(2.3)
Indeed, for everyn∈Z, we have by the definition ofrnthat, for everyk≥0 andλ∈[rn+k+1,rn+k),
(2.4)
Sinceλ An⊂{x∈Ω:|f(x)|>λ}. Combining this and Lemma 2.2, we then deduce that, for everyk≥0,n∈Z, andλ∈[rn+k+1,rn+k), Hence, we deduce that, for everyk≥0,n∈Z, andλ∈[rn+k+1,rn+k), (2.5) which, together with (1.3) and (2.4), implies that, for everyk≥0 andn∈Z, For everyq∈[1,∞), by the above inequality, we have, for everyn∈Z, Thus, we conclude that, for everyn∈Z, By summing this and interchanging the summation signs, we have This proves (2.2) for the caseq∈[1,∞). For the caseq=∞, by the definition ofrn, (2.5) and (1.3), we know that, for everyn∈Z, Thus, we have This proves (2.2). Then, (2.3) follows by repeating above steps. This proves the above claim. By monotonicity, the triangle inequality ofL1-norm and the symmetry, we have (2.6) Since, for everyn∈Z, φ({x∈Ω:rn+1<|f(x)|≤rn})≤φ({x∈Ω:rn+1<|f(x)|})≤2n+2, it follows from (1.3) that Using this, we then deduce that (2.7) By Lemma 2.2, we have, for everyk≥0, and It then follows that, for everyn∈Zandk≥0, By the above inequality, the Hölder inequality and the Minkowski inequality inlq, we have Observe that, for everyn∈Z, (see [19]). By this observation, (2.2) and (2.3), we conclude that A combination of this, (2.6) and (2.7) yields the assertion. Remark 2.3Letφbe a Musielak-Orlicz function. (i) If conditions (1.2) and (1.3) are replaced by the following conditions that there exists a positive constantCsatisfying, for everyf∈Lφ,q(Ω) andλ>0, μ({|f|>λ})≤Cφ({|f|>λ}) (2.8) and then the conclusion in Theorem 1.1 holds true. Indeed, in the above proof, we only used (1.2) and (1.3) for the set {|f|>λ}. then the conclusion in Theorem 1.1 also holds ture. Now we give a sufficient condition to ensure that (1.2) and (1.3) hold true. (2.9) and (2.10) then (1.3) holds true. (2.11) and (2.12) Ifφ(A)≥Cφ, we haveφ(A)1/p0≥1. Sinceφis of uniformly lower typep0onA, it follows that Sinceφis of uniformly upper typep1onA, it follows from above inequality that Combining this with (2.9) and Lemma 2.2, we then deduce that Thus, we conclude that, for every measurable setA, On another hand, for every measurable setAwithφ(A)≤Cφ, we have Sinceφis of uniformly lower typep0onA, it follows that that is, Combining this inequality and (2.12), we then deduce that It follows that A combination of this with (2.10) and Lemma 2.2 yields that The desired conclusion follows from this and the above paragraph. Remark 2.5Letφbe a Musielak-Orlicz function. (ii) Condition (2.9) is equivalent to the following: there exists a positive constantKsuch that φ(Ω)≤K. (2.13) Indeed, (2.13) follows immediately from (2.9). Conversely, A combination of (2.13) and Lemma 2.2 yields (2.9). Thus, condition (2.9) holds if and only ifφ(·,1)∈L1(Ω). To better understand these conditions in Lemma 2.4, we consider them in several special examples. In the weighted Lebesgue spaces,φ(x,t)∶=w(x)tp,p≥1, for anyx∈Ω andt∈(0,∞). We haveφis of uniformly lower and upper typep. Hence, (2.9) and (2.10) hold trivially. Letp(·) be a measurable function on Ω satisfying (2.14) In the variable Lebesgue spaces,φ(x,t)∶=tp(x) for anyx∈Ω andt∈(0,∞). We haveφis of uniformly lower typep-and of uniformly upper typep+. If (Ω,F,P) is a probability space, then (2.9) holds trivially, and (2.10) is equivalent to (2.15) However, ifp(·) is a variable exponent and (2.15) holds for all sets, thenp(·) is a constant, see [14] for the details. So we have to suppose that theσ-algebraFare generated by countable atoms and (2.15) holds for all (set) atomsA. The above inequality then becomes the analogy of the local log-Hölder continuous condition in probability space setting. But until now, we can not ask (1.3) only for atoms. Thus, the conditions of Lemma 2.4 can not cover the variable case. Furthermore, we still can not find an example to ensure that (2.9) and (2.10) hold true whenp-(A) Similarly, in the Orlicz spaces,φ(x,t)∶=Φ(t) for anyx∈Ω andt∈(0,∞), where Φ is an Orlicz function. In this caseφ(A)=P(A)Φ(1). It follows that Φ satisfies (2.15) if and only if Φ satisfies (2.10). Now, we provide the condition to fulfill (1.2). Lemma 2.7Letφbe a Musielak-Orlicz function. If infx∈Ωφ(x,1)=∶φ-∈(0,∞), then (1.2) holds true. ProofSince, for everyx∈Ω,φ(x,0)=0, it follows that, for every measurable setA, φ(x,1A)≥φ(x,1)1A≥φ-1A. It follows that This finishes the proof. Now we provide the proof of Corollary 1.3. see, for instance, [19]. Moreover,φis of uniformly lower type and upper typep. By Remark 2.6 and Lemma 2.4, we deduce thatφsatisfies (1.3). Sinceω∈A∞(Ω), it follows from [6] that, for every measurable setA, Observe thatωis integrable and Ω is finite. By this observation and the above inequality, we conclude that |A|ω(A)=φ(A). Therefore, this specialφsatisfies (1.2). A combination of this fact with the above paragraph and Theorem 1.1 yields the assertion. By Remark 2.6, we know that Theorem 1.1 can not easily cover the Orlicz case. To complete the proof of Theorem 1.1 in this section, we prove the Hölder inequality for Lorentz type space in Orlicz setting. Let Φ be an Orlicz function andq∈(0,∞). The Orlicz-Lorentz spaceLΦ,q(Ω) is defined to be the set of all measurable functionsfsatisfying The left inverse function Φ-1of an Orlicz function Φ is defined by setting, for everyt∈(0,∞), Φ-1(t)∶=inf{τ≥0:Φ(τ)≥t}. If Φ is strictly increasing and continuous function on (0,∞), then Φ-1is just normal inverse function of Φ. The following proposition completes Theorem 1.1. Proposition 3.1Let Φ be an Orlicz function andq∈[1,∞). If Φ is of lower typep0for somep0∈[1,∞) and of upper typep1for somep1∈(1,∞), then there exists a positive constantCsuch that where Ψ is the conjugate function of Φ. ProofBy [9], we know that, for anyt∈(0,∞), Φ-1(t)Ψ-1(t)≈t. It was proved in [7] that which, together with the above inequality, implies the assertion. We finish this paper by the following remarks. Remark 3.2According to Proposition 3.1, we know that the conditions (1.2) and (1.3) in Theorem 1.1 are redundant in the Orlicz setting. Moreover, in the caseφ(x,t)∶=Φ(t) for anyx∈Ω andt∈(0,∞), (1.3) holds if and only if there exists a positive constantCsuch that, for any measurable setA, This is because of the fact that see [7] for details. Remark 3.3Letφbe a Musielak-Orlicz function andq∈[1,∞). (i) Based on the Hölder inequality established in this paper, we believe that the dual space of generalized Orlicz-Lorentz spacesLφ,q(Ω) is given by the conjugate modularsφ*andq′, that is the spaceLφ*,q′(Ω). (ii) Following the idea of [19], using (i), we can establish the Burkholder-Gundy inequalities for generalized martingale Orlicz-Lorentz spaces. But we do not pursue it here. Remark 3.4It was mentioned in the introduction that optimal contant of the Hölder inequality was obtained in [15]. However, in terms of interaction of the variability inxandtthe present assumptions and constants are far from optimal. Whether the better assumptions and contants exist is a question for future research.
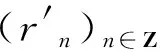

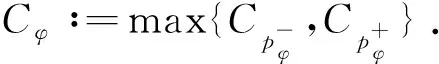
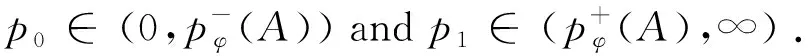

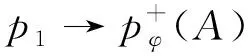
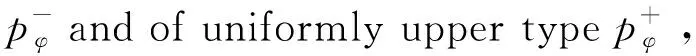
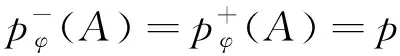
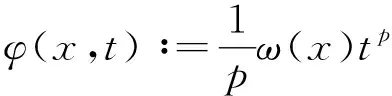
3 Hölder’s inequality for Orlicz-Lorentz spaces