领悟教材中之法 破解教材外之题——以一道2019年全国高考真题多视角解析为例

杜海洋

(四川省成都经济技术开发区实验中学校 610000)

很多时候我们与学生交流时，学生最爱说的一句：“课堂上我听得懂，就是课后做不来题.”这应该是让我们老师极其尴尬的，说得直白点，就是学不会，你也没策嘛！笔者发现导致其主要原因是一部分老师重结果轻过程，另就是学不致用，导致讲与练脱节，未将学生就近学习区思维激活起来.下面笔者就以在讲完解三角形这章内容进行复习时，选了一道高考试题进行多视角解答，浅议结合教材知识学以致用，以飨读者.

(1)求B；

(2)若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

选题理由(1)本题考查三角形的正弦定理和余弦定理、面积公式的运用，考查三角函数的恒等变换，以及化简运算能力，最后考查△ABC是锐角三角形这个条件的利用.由于题目所求是范围问题，又涉及到锐角三角形，所以在解答中突出解法的灵活性、开放性及细微性，考查很全面，又涉及本章主干知识，是一道经典的代表题.

(2)一道高考试题具有权威性，一方面体现本章知识在高考中的地位程度，另一方面容易让学生在课堂学习认真度极大提高.

(3)对于第(1)问求角，这应是正弦定理或余弦定理的边角互化的直接体现，由于等式各项的边为一次型，即本问首选采用正弦定理边化角的处理策略.对于第(2)问，我们首先会感悟函数求最值或值域常用的方法有:函数单调性法、不等式法、图象法、坐标法等等，尤其是三角函数的特殊性有没有破解这类问题“自身”的“独门绝技”？高中三角函数的定义可是单位圆引入的哦，三角函数图象用到圆，正弦定理的推导也用到三角形的外接圆，其实余弦定理推导也可用到圆等等，可见三角形与圆形影不离，那么这类题可以借用圆解不？下面笔者就从这几个不同的方面对此题进行探究.

探究一研读题意同学们发现第(1)问难度不大，运用三角函数的诱导公式和二倍角公式，以及正弦定理，计算可得所求角.

视角一、目标函数法

方法一以边为目标函数

评注建立不等式求最值或值域是常见的一种处理策略，尤其是均值不等式的运用.本法通过将面积转化为某一边的函数，利用了锐角三角形这一条件，通过余弦定理建立不等式组来确定a的范围，从而求得结果.由于此法涉及只有一边，并且边的次数为1，发现均值不等式不能奏效况且为锐角三角形，均值不等式直接控制不了“最大值”或“最小值”.本法体现了余弦定理典型的灵活运用.

方法二以角为目标函数

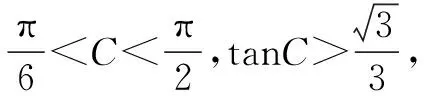
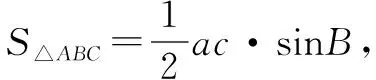
反思三角形涉及边和角两大核心要素，由以上两种解法我们体会到：题设尤其前提已知三角形是锐角、钝角三角形时，知道一边和一角求面积、周长或两边和与比等最值或值域，则隐含地告诉学生可以建立以角(边)为变量的函数，但建立以角为目标函数成为解决这类问题的通法.体现了属于典型的转化化归的数学思想

探究二我们深知一个定理或公式的得来，其推导方法及思想更重要，可以说重要的程度远远超过这些定理或公式.尤其在推导正弦定理时的平面几何法，以及外接圆法思想应该记忆犹新，自然会想到这两种方式都能推出正弦定理，可以大胆运用此思路试做！

视角二、几何法

解法三平面几何作图法(秒杀1).

评注数学来源于生活，我们深知数学很多的结论可以通过数学实验来验证或完成.尤其三角形三内角和定理，三边关系，圆锥曲线等定义或结论,通过实验让学生身临其境感受数学魅力.本法可以说是一次“实践出真知”.

解法四外接圆法(秒杀2)

类比法三，因为由已知条件知道角B和边c，又因为所求的是锐角三角形即联想直角三角形是其临界点，则构造以AB为直径的圆，同理易得当AC与圆弧AD相交或AC成为圆的切线时，此时点C为其临界点，以下解法同法三.

评注单位圆或三角形的外接圆是解决涉及三角形已知一角和边(不管角与边是否相对)求有关边、角、周长或面积的最值(值域)的快速解法，尤其是三角形给出锐角或钝角三角形的约束条件，利用此法可快速破解!

反思通过方法三、四我们真正体会到领悟教材定理、例题的解题方法及思路是解答问题的根本之源.这也是我们常常倡导不要“重结果，轻过程”的缘由吧！

探究三数形结合法是我们研究高中数学不可缺少的一种有效手段，坐标法是数形结合的真正体现，坐标法的优越性可将复杂的线段或角的关系转化为纯数据处理，从而避免了图形思维的难度.当然恰当的建系可为运算带来简便，提高解题速度.

视角三、数形结合法

解法五坐标法

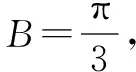
评注坐标法是高中数学中典型的数形结合方法体现，坐标法主要功能是将复杂的几何关系转化为“数”建立方程或不等式进行计算.解三角形用坐标法其中如何建系尤为重要，一般将已知角的顶点作为坐标原点为关键步骤，当然尽可能将其中一边放在坐标轴上，本法将a边与x轴重合的目的是点A的坐标易求.

探究四在证明余弦定理、两角差的余弦公式时再次体现了平面向量工具性的强大作用，那么就应该活学活用，现学现用.让学生真正体会教材定理、例题蕴含的知识宝库！

视角四、向量法

解法六(向量法1)

同法五要使△ABC为锐角三角形，即cosA>0，cosC>0.由向量

解法七(向量法2)

评注向量与三角密不可分，正弦定理、余弦定理的证明，两角差的余弦公式推导等都把向量的工具性体现得淋漓尽致，尤其要注意a·b>0时，两向量的夹角可为0°等一些特殊情况.

反思由本例的几种角度探究我们体会到方法来源于教材，其中解法不只是教材的定理、性质等直接运用，还包括推导这些定理、性质的方法与思路的再现.这就是典型的活学活用，现学现用！真正让学生重视课本、领悟课本精髓而又不拘泥课本.

细心的读者发现这是典型的“子母题”.(请读者根据以上提供的几种思维方法进行解答，笔者发现此题利用三角形外接圆可以“秒杀此题”)

总之，教学要重视教材，提炼教材的精华，要将教材的思维方法付诸实施，才能让学生感受解题有本之根！解三角形问题离不开边和角，涉及一边和一角、一角和两边关系等、因为边角的互化关系，最终可将问题化归为边或角达到归一，这就是我们常说类型题解法的“大格局”. “多想少算”是当今高考命题一大亮点，尤其在解答一些小题时可结合运动观点进行最值或值域的妙解，如采用的单位圆法，外接圆法，隐形圆法等可以“秒杀”此类问题.一题一世界，选择高质量的试题进行探究，知一题懂一类.“刷”高质量的代表题，真正让学生摆脱“题海”，以不变应万变，决胜高考！总之：解三角形是高考考查的重点和热点，尤其面积与正余弦定理的结合每年必考，所以我们平时不但要对基本公式熟练掌握，还有对通性通法进行灵活运用.以上介绍的解法仅是涉及能转化为求边或角的值或值域的一些基本方法与教材同源，同学们需要平时学习中从教材探索总结才能不断地变通及提高学习效率.