从属于贝形区域的一类逆函数的三阶 Hankel 行列式

郭栋，李宗涛

（1.滁州职业技术学院基础部，安徽滁州239000； 2.广州民航职业技术学院人文社科学院，广东广州510403）

1 引言及预备知识

令H 表示单位圆U={ z :| z|＜1}内具有下述形式的单叶函数的全体

H中的所有的单叶函数记为S.

Sakaguchi[1]引入了关于对称点的星象函数类Ss*，满足条件：

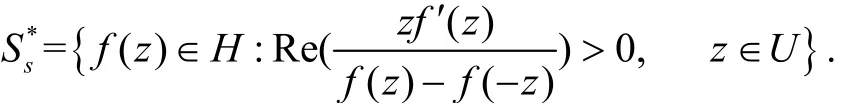
Noonan 和Thomas[2]首次引入函数f(z)的q阶Hankel 行列式：

其中 a1=1,m≥1,q ≥ 1. 当m, q 取一些特殊值时，可得

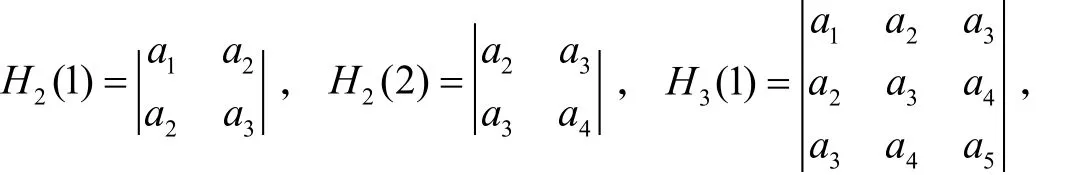
则有H3(1)=a3H2(2)-a4(a4-a2a3)+a5H2(1).

部分作者[2-5]研究了许多解析函数类上的H2(2)行列式. 最近一些作者[6-9]研究了解析函数类上的H3(1)行列式，得到了其上界. 受此启发，本文构造一类从属于贝形区域的解析函数类，研究其上f-1的H3(1)行列式.

定义1[10]函数q ( z )= 1+ z2+ z 将单位圆盘映射为右半平面的贝形区域，在C {i, -i }单叶解析，区域关于实数轴对称. 此函数是一个正实部函数 q(0)=q′(0) = 1.

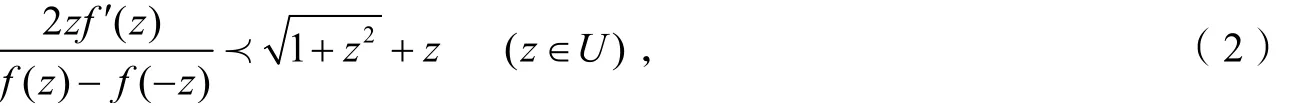
记函数f ( z )∈Ls( q).

引理1[11]假设p ( z ) = 1+p1z+p2z2+⋅⋅⋅在内解析，满足Re p ( z ) ＞ 0，则

引理 2[12]假设p ( z ) = 1+p1z+p2z2+…在U={ z :| z|＜1}内解析，满足Re p ( z) ＞ 0，则存在复数y、 z (| y|≤1,| z|≤ 1,)，有

引理 3[13]假设p ( z ) = 1+p1z+p2z2+⋅⋅⋅在U={ z :| z|＜1}内解析，满足Re p ( z ) ＞ 0，则

2 主要结果

定理1如果f ( z )∈Ls( q)且是f 的逆函数，则有

证明如果f ( z )∈Ls( q)，那么存在解析函数，使得

成立.

由式（3～5）得

因为

是f 的逆函数，则有

由式（10）和（11），可得

由式（11）和（12），可得

比较两边的系数得

由上式及式（6～9）得

由引理1 及式（13～16）可得定理1.

定理2如果是f 的逆函数，则有

证明由式（13）和（14）及引理3 得

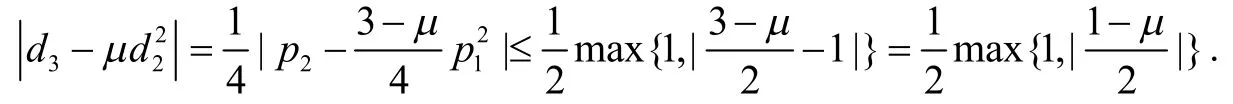
定理3如果f ( z )∈Ls( q)且是f 的逆函数，则有

证明由式（13～15）及引理2 得

令| p1|=p(0≤ p ≤ 2)，由三角不等式上式子化为

定理4如果f ( z )∈Ls( q)且是f 的逆函数，则有

证明由式（13～15）及引理2 得

令| p1|=p(0≤ p ≤ 2)，由三角不等式上式化为

下面需要求 G ( p, | y |)在闭区域 Ω={( p, | y|):0≤ p≤2,0 ≤|y |≤1}上的最大值.2)| |)y . 令，得2p= 或

定理5如果f ( z )∈Ls( q)且是f 的逆函数，则有

证明由于，则由不等式得

由式（17）及定理1、2、3、9 可得定理5.