任意跨宽比三点弯曲梁断裂力学参数的权函数法求解

童第华, 吴学仁, 赵晓辰,2, 徐 武, 胡本润,2

（1.中国航发北京航空材料研究院 检测研究中心，北京 100095；2.中国航空发动机集团 材料检测与评价重点实验室，北京100095；3.上海交通大学 航空航天学院，上海 200240；4.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连116024；5.航空材料检测与评价北京市重点实验室，北京 100095）

矩形截面三点弯曲梁是断裂力学中最常见的裂纹几何之一，它不但是一种常用的材料断裂韧度和疲劳裂纹扩展速率测定的标准试样[1]，也是许多工程结构的一种重要部件。该部件裂纹问题的应力强度因子（SIF）和裂纹嘴张开位移（CMOD）等断裂力学关键参量最早是由Gross和Srawley[2-4]利用边界配置法（BCM）针对特定的跨宽比（S/W = 4）给出的，并被长期应用至今。后续研究工作还计算了该试样的加载点位移[5-6]。Kaya和Erdogan利用奇异积分方程方法给出了S/W = 4的高精度应力强度因子（SIF）和裂纹嘴张开位移（CMOD）[7]。Bakker[6]通过严格的推导给出了S/W = 4试样的宽范围解析解，并结合有限元分析对SIF和CMOD的精度进行了全面评价。

材料断裂性能的测定通常采用S/W = 4的三点弯曲标准试样，而工程结构中的S/W比值则是任意的。任意跨宽比（S/W）三点弯曲梁的高精度SIF和CMOD解是对构件进行断裂力学分析的前提。尽管Fett[8]利用BCM求得的权函数分析了不同S/W值的应力强度因子和加载点位移，但是加载点位移不便于实际使用，而裂纹嘴张开位移则更容易通过实验测定。

本工作针对任意跨宽比S/W的三点弯曲梁，利用Wu（吴学仁）-Carlsson[9-11]解析权函数法求得宽范围无量纲裂纹长度（0 ≤ α ≤ 0.85）的高精度SIF和CMOD解。求解中所需的裂纹面应力分布由Filon的经典解析公式计算得到[12]，进而通过对解析权函数法结果的多元线性回归，确定三点弯曲梁任意跨宽比S/W值（S/W＝2～16）的宽范围SIF和CMOD表达式。最后对解析权函数法在黏聚断裂韧度计算中的应用做简单讨论。

1 利用解析权函数法求解SIF和CMOD

1.1 有限宽板边缘裂纹的Wu-Carlsson解析权函数

根据断裂力学的权函数理论，SIF可以通过对权函数m（a, x）与假想裂纹处的应力分布σ（x）的乘积进行积分而求得，见式（1）[9-11]。权函数m（a, x）仅与裂纹几何（包括载荷-位移边界条件）有关。

式中： a和x分别是裂纹长度和沿裂纹的坐标。

对于边缘裂纹，坐标x的原点位于裂纹嘴处。为便于推导，引入无量纲量：α= a/W，=x/W和σ（）/σ0。其中σ0为名义应力，W为板宽，如图1所示。

于是式（1）可以写成：

三点弯曲梁属于典型的有限宽矩形板边缘裂纹，其解析权函数m（α/α）已由 Wu-Carlsson及其合作者给出（L/W≥ 2）[9-11]。注意图1中的板长度L有别于跨距S。鉴于本工作考虑S/W≥ 2，则肯定有L/W≥ 2。该解析权函数m（α/α）的无量纲级数展开式为：

图1 三点弯曲梁Fig. 1 Three-point bending beam

式中：函数Fi（α）是根据文献[9-11]中的规范化解析权函数法，利用有限宽矩形板边缘裂纹在一种参考载荷下的SIF和CMOD已知解确定的。基于这些Fi（α），就能够通过式（3b）得到系数βi（α），于是就能最终确定式（3a）的权函数m（α/α）。该权函数的精度已经过严格验证。有关推导和验证的具体细节可参见文献[9-11]。

为方便使用，文献[10-11]给出了有限宽板边缘裂纹权函数的βi（α）系数（式（3b））的高精度拟合表达式：

1.2 用权函数法求解复杂应力作用下的应力强度因子

对有限宽板边缘裂纹的解析权函数m（α,/α）与无裂纹体在假想裂纹位置的应力分布σ（x）的乘积按式（2）进行积分，便能求得在任意σ（x）作用下的应力强度因子K。在工程实际中，一个非常简便有效的通用方法是用多项式来表达复杂的σ（x）分布，其中的每一项则可以表示为式（4）的幂函数（n为正整数）分布应力（图2）：

将式（4）和式（3）代入式（2）中，就能得到幂函数分布应力下的无量纲应力强度因子fn的封闭解[9-11]：

按式（5）求得的fn值见表1。

对于裂纹面受多项式分布应力的情况：

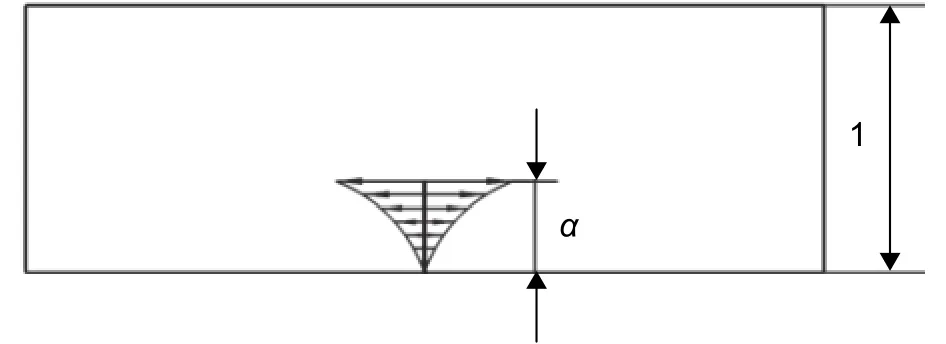
图2 裂纹面受幂函数分布应力Fig. 2 Crack line power stress loading

表1 由式（5）得到的裂纹面幂函数应力σ（）/σ0=n（n = 0～6）引起的无量纲应力强度因子fnTable 1 Non-dimensional SIF fn for crack line power stress σ（）/σ0=n（n = 0-6）determined by Eq（5）.

表1 由式（5）得到的裂纹面幂函数应力σ（）/σ0=n（n = 0～6）引起的无量纲应力强度因子fnTable 1 Non-dimensional SIF fn for crack line power stress σ（）/σ0=n（n = 0-6）determined by Eq（5）.

n α 0 1 2 3 4 5 6 0.01 1.1226 6.8236×10-13 5.2464×10-5 4.4008×10-7 3.8597×10-9 3.4771×10-11 3.1888×10-13 0.05 1.1402 3.4471×10-2 1.3217×10-3 5.5346×10-5 2.4245×10-6 1.0913×10-7 5.0012×10-9 0.1 1.1890 7.0886×10-2 5.3978×10-3 4.5017×10-4 3.9331×10-5 3.5335×10-6 3.2339×10-7 0.2 1.3672 1.5577×10-1 2.3174×10-2 3.8112×10-3 6.5968×10-4 1.1774×10-4 2.1441×10-5 0.3 1.6602 2.6753×10-1 5.7829×10-2 1.3985×10-2 3.5821×10-3 9.4960×10-4 2.5749×10-4 0.4 2.1113 4.2491×10-1 1.1788×10-1 3.7080×10-2 1.2447×10-2 4.3438×10-3 1.5552×10-3 0.5 2.8241 6.6303×10-1 2.2011×10-1 8.4007×10-2 3.4501×10-2 1.4810×10-2 6.5452×10-3 0.6 4.0333 1.0583 4.0145×10-1 1.7748×10-1 8.5181×10-2 4.2987×10-2 2.2429×10-2 0.7 6.3558 1.8100 7.5861×10-1 3.7524×10-1 2.0330×10-1 1.1657×10-1 6.9437×10-2 0.8 11.9548 3.6179 1.6315 8.7726×10-1 5.2096×10-1 3.2956×10-1 2.1773×10-1 0.85 18.6264 5.7758 2.6786 1.4869 9.1465×10-1 6.0119×10-1 4.1376×10-1 0.9 34.6348 1.0967×101 5.2027 2.9615 1.8731 1.2691 9.0252×10-1

相应的无量纲应力强度因子不需进行数值积分，仅通过简单的四则运算就能求得：

1.3 用权函数法求解裂纹张开位移

除SIF外，受任意载荷作用下的裂纹面张开位移（COD）和裂纹嘴张开位移（CMOD）也可用权函数法方便地求得[9-11]。根据权函数m（α,/α）与裂纹面位移u（α/α）的关系，结合裂纹尖端条件u（α/α= 0）=0，通过对式（8）的积分，有：

将式（3）的权函数m（α/α）和式（2b）的f代入式（8）中，得到任意载荷下的COD：

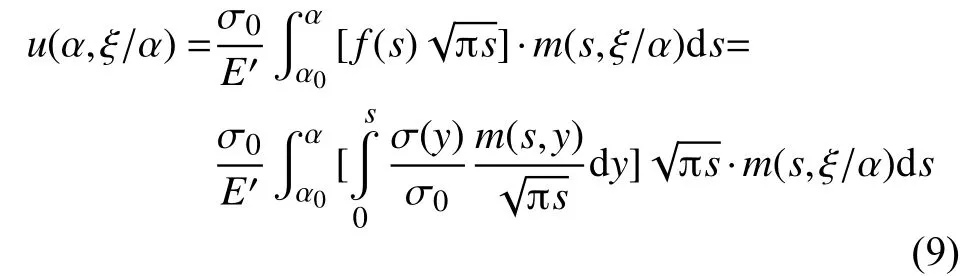
在许多情况下，从实验的角度考虑CMOD比COD更为重要。利用式（9）能够方便地计算得到CMOD。对于幂函数分布应力情况σ（）/σ0=n, 记相应的 CMOD 为Vn（Vn=u（α/α= 0）E'/（σ0α）），则有：

根据式（10）计算的裂纹面受幂函数分布应力σ（）/σ0=n作用下的 CMOD 见表 2。

利用这些值, 采用类似于式（7）计算SIF的方法，就能通过简单的四则运算得到在多项式分布应力（式（6））作用下的 CMOD：

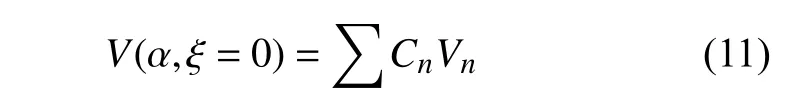
2 任意跨宽比S/W三点弯曲梁的无裂纹应力计算

利用权函数法计算应力强度因子和裂纹面张开位移，除了需要该裂纹几何的权函数m（α/α）（式（3））外，还需要无裂纹体中假想裂纹处的无量纲应力分布σ（）/σ0。无裂纹的σ（）/σ0计算属于常规的弹性力学问题，一般可通过有限元等数值方法计算得到，但对于本工作考虑的任意S/W三点弯曲梁（图1），由于集中力加载导致的奇异性，即使采用高度细分的有限元网格也很难给出＝1.0区域的高精度应力分布。Filon对任意跨宽比S/W三点弯曲梁的无裂纹应力给出了经典的解析解[12]，即式（12）的无穷级数：

表2 由式（10）得到的裂纹面幂函数应力σ（）/σ0=n（n = 0～6）引起的无量纲裂纹嘴张开位移CMOD：V（α/α = 0）=u（α/α = 0）E'/（σ0α）Table 2 Non-dimensional CMOD for power stresses σ（）/σ0=n, V（α/α = 0）= u（α,/α = 0）E'/（σ0α）, determined byEq（10）

表2 由式（10）得到的裂纹面幂函数应力σ（）/σ0=n（n = 0～6）引起的无量纲裂纹嘴张开位移CMOD：V（α/α = 0）=u（α/α = 0）E'/（σ0α）Table 2 Non-dimensional CMOD for power stresses σ（）/σ0=n, V（α/α = 0）= u（α,/α = 0）E'/（σ0α）, determined byEq（10）

n α 0 1 2 3 4 5 6 0.01 2.9127 8.8592×10-3 4.5425×10-5 2.8583×10-7 2.0058×10-9 1.5059×10-11 1.1838×10-13 0.05 2.9632 4.5292×10-2 1.1640×10-3 3.6674×10-5 1.2880×10-6 4.8382×10-8 1.9026×10-9 0.1 3.1026 9.6129×10-2 4.9725×10-3 3.1450×10-4 2.2143×10-5 1.6665×10-6 1.3123×10-7 0.2 3.6592 2.3602×10-1 2.4849×10-2 3.1738×10-3 4.4965×10-4 6.7961×10-5 1.0736×10-5 0.3 4.7001 4.7430×10-1 7.6079×10-2 1.4687×10-2 3.1349×10-3 7.1269×10-4 1.6920×10-4 0.4 6.5374 9.0944×10-1 1.9634×10-1 5.0714×10-2 1.4453×10-2 4.3833×10-3 1.3877×10-3 0.5 9.8973 1.7566 4.7518×10-1 1.5328×10-1 5.4510×10-2 2.0629×10-2 8.1505×10-3 0.6 16.6091 3.5619 1.1510 4.4315×10-1 1.8821×10-1 8.5119×10-2 4.0214×10-2 0.7 32.2131 8.0118 2.9870 1.3284 6.5276×10-1 3.4200×10-1 1.8740×10-1 0.8 79.9443 2.2331×10-1 9.3447 4.6773 2.5934 1.5365 9.5360×10-1 0.85 149.6840 4.3872×10-1 1.9274×10-1 1.0145×10-1 5.9244 3.7013 2.4248 0.9 355.1260 1.0858×10-2 4.9789×10-1 2.7395×10-1 1.6748×10-1 1.0969×10-1 7.5418

式（12）中的级数展开项数n的选择取决于对求解精度的要求。经过收敛性分析，取n= 100和125得到结果差别在0.15%以内, 故这里对式（12）取n= 100。结合工程结构三点弯曲梁的典型情况，本工作考虑梁的跨宽比为S/W= 2～16。具体计算中取S/W= 2、4、8和16作为示例，根据式（12）计算的无裂纹应力分布σ（ξ）/σ0，见图3。

图3 不同跨宽比S/W三点弯曲梁的无裂纹应力分布，由Filon式（12）求得（n = 100）[12]Fig. 3 Un-cracked stress distribution for three-point bending beam, using Filon’s expression (12) with 100 terms[12]

把以上计算得到的假想裂纹处的应力分布拟合为式（13）所示的多项式形式（0 ≤≤ 0.95）：

式中的系数Cn见表3。

3 任意跨宽比S/W三点弯曲梁的SIF和CMOD

三点弯曲梁受式（13）所示多项式形式的裂纹面应力分布，其SIF和CMOD可以很简单地通过式（7）和式（11）确定（Cn、fn和Vn分别见表 3、表 1和表2）。按此求得的SIF和CMOD结果分别见表4、表5和图4。对于S/W= 4情况，与Kaya和Erdogan[7]、ASTM[1]、Bakker[6]，Guinea 等[13]和 Fett[8]的结果做了广泛比较。本工作计算结果与文献中公认的Kaya和Erdogan[7]高精度结果最为接近，SIF和CMOD的最大差异分别为0.27%和0.39%。而对于α= 0.2～0.4的 CMOD解，ASTM[1]中的Srawley公式和Guinea等[13]给出的结果与Kaya和Erdogan[7]的相对误差均超过1.0%。当裂纹长度较小时（α＜ 0.2），ASTM[1]中的 Srawley 公式过高估计了SIF，这与Bakker[6]的结论完全一致。这表明利用解析权函数法能够快速求得任意跨宽比S/W的三点弯曲梁的高精度SIF和CMOD。而这种方法的计算效率则是有限元法的103～104倍，且不需要数值解法所需的建模经验。

为确定任意跨宽比S/W的三点弯曲梁的SIF和 CMOD，这里基于式（7）和式（11）的计算结果，结合理论极限值：α= 0为f（α）（1-α）3/2=1.0731，V（α）（1-α）2= 2.7832；α= 1.0 为f（α）（1-α）3/2=0.37384，V（α）（1-α）2= 1.3172，拟合得到了以下高精度表达式（拟合偏差小于1%），其适用范围为0 ≤α≤ 1.0, 2 ≤S/W≤ 16。

式中：系数λi和χi（i= 0,1…,6）为：

表3 式（13）三点弯曲梁σ（）/σ0的应力多项式系数CnTable 3 Crack line stress polynomial coefficients Cn for three-point bending beam in Eq.（13）

表3 式（13）三点弯曲梁σ（）/σ0的应力多项式系数CnTable 3 Crack line stress polynomial coefficients Cn for three-point bending beam in Eq.（13）

Cn S/W 10 12 16 0 2 4 6 8 0.9303 0.9530 0.9686 0.9758 0.9812 0.9846 0.9884 1-2.6150 -2.2367 -2.1574 -2.1135 -2.0966 -2.0846 -2.0649 2 2.4415 1.1596 0.7733 0.5721 0.4717 0.4063 0.3115 3-1.3218 -0.6728 -0.4493 -0.3331 -0.2763 -0.2412 -0.1875

表4 三点弯曲梁SIF和CMOD的比较，S/W = 4Table 4 Comparison of SIF and CMOD for three-point bending beam, S/W = 4

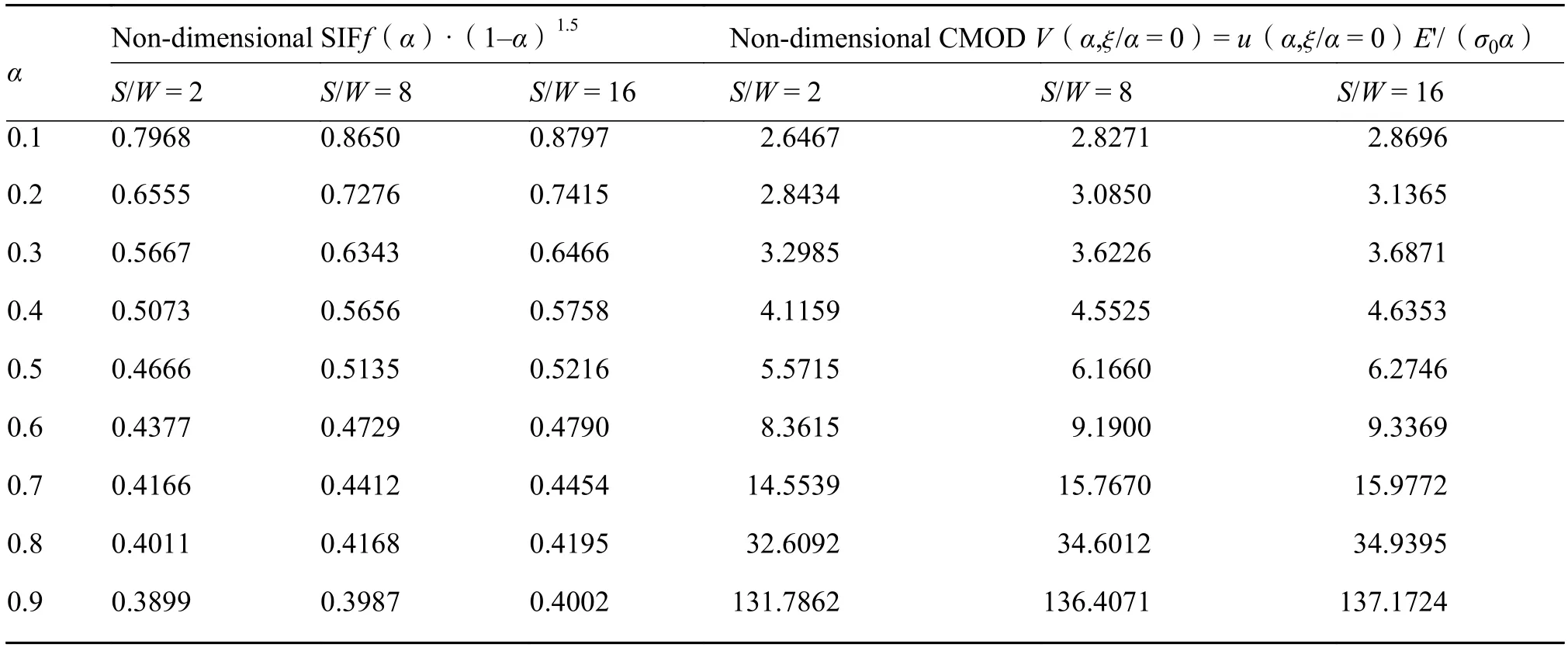
表5 三点弯曲梁的SIF和CMOD，S/W = 2, 8和16Table 5 SIF and CMOD for three-point bending beam, S/W = 2, 8 and 16

为了在实验中方便地测量裂纹长度，需要得到无量纲裂纹长度α和CMOD之间的柔度关系式。通过式（14d）进行逆运算得到相应的柔度关系如图4（b）所示。图4（b）中也把本文的结果与Guinea等[13]根据插值方法得到的2.5 ≤S/W≤ 16柔度关系式（15）做了比较，二者的差别在1%之内。

4 三点弯曲梁的黏聚断裂韧度计算

作用在裂纹尖端后方的黏聚应力起着约束裂纹张开和阻滞裂纹扩展的作用，如图5所示。它所引起的黏聚断裂韧度（KIC，c，为负值）对于脆性材料的断裂准则研究十分重要。由于KIC，c直接影响起裂断裂韧度KIC，ini计算结果的准确性（KIC，ini＝KIC，un-KIC，c，KIC，un为失稳断裂韧度），其求解计算被认为是确定混凝土双K断裂韧度的核心环节[14-16]。而计算黏聚断裂韧度KIC，c则需要相关裂纹几何的权函数（或格林函数，二者仅差一个系数(πα)1/2）。文献中对三点弯曲梁试样即有限宽矩形板边缘裂纹的黏聚断裂韧度计算问题有较多讨论[15-17]，但值得注意的是，这些文献普遍采用了著名的Tada-Paris-Irwin早期应力强度因子手册[18]中作用在裂纹面任意位置的一对集中力P引起的K解公式，即式（16）的格林函数：

为便于积分，文献[17]还用式（17a）的“通用权函数” 表达式对式（16b）进行了最小二乘拟合（拟合偏差 ＜ 1.5%）。

与式（17a）对应的格林函数为：

式中的系数M1-4见文献[15，17]。

本文作者在文献[10-11]中采用多种方法，对有限宽矩形板边缘裂纹的各种权函数的精度做了综合验证和评价，发现式（16）和式（17）的精度存在较大问题：其误差与α和ζ/α有关，局部最大值超过了15%，并非所称的2%[17-18]。这必然会明显影响KIC，c和后续KIC，ini的计算精度。

图4 三点弯曲梁（S/W = 2, 4, 8, 16和纯弯曲）的SIF和CMOD的比较Fig. 4 Comparison of SIF and CMOD for three-point bending beam（for S/W = 2, 4, 8, 16 and pure bending）（a）SIF；（b）CMOD

利用文献 [9～11] 的权函数（即本文式（3）），可以很方便地计算黏聚应力引起的黏聚断裂韧度KIC，c。在图 5（a）中，当裂纹面的任意区段受任意区段的线性分布应力作用时, 可以把该应力写为：

图5（a）中的区段线性分布应力引起的无量纲应力强度因子为[9-11]：

图5 裂纹面受区段线性应力和两种黏聚应力分布（a）裂纹面受区段线性应力；（b）第一种黏聚应力分布；（c）第二种黏聚应力分布Fig. 5 Linear stress segment acting on part of the crack and two cohesive stress distributions（a）linear stress segment acting on part of the crack；（b）the first cohesive stress distribution； （ c） the second cohesive stress distribution

利用式（18）和（19），可以方便地求得图 5（b，c）的两种黏聚应力分布引起的黏聚断裂韧度KIC，c。

5 结论

（1）利用有限宽板边缘裂纹的Wu-Carlsson解析权函数，结合无裂纹应力分布的Filon解析解，根据三点弯曲梁的无裂纹应力分布的多项式系数和幂函数应力下的权函数封闭解，通过简单的四则运算，求得了跨宽比S/W= 2、4、8、16和∞的三点弯曲梁的应力强度因子和裂纹嘴张开位移；其中，S/W=4的计算结果与公认的Kaya和Erdogan积分方程解高度一致。针对工程应用需求，给出了任意跨宽比的宽范围应力强度因子和裂纹嘴张开位移的拟合表达式。

（2）对利用权函数法计算材料的黏聚断裂韧度KIC，c做了讨论，指出了文献中所采用的Tada-Paris-Irwin早期手册中的格林函数及其后续拟合的权函数公式的精度问题，以及对计算结果的影响。