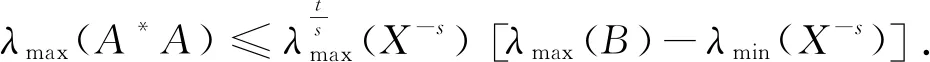算子方程正算子解的性质

赵转萍

(山西大学商务学院 数学教学研究部,山西 太原 030031)

算子方程作为泛函分析的一个重要组成部分，它在最优化理论，控制论以及统计学等方面都有广泛应用.一直以来，许多国内外数学家在有限维空间中，利用矩阵理论对算子方程的解进行研究，得出了一系列深刻的结论[1-5]，并将这些结论推广到了无限维Hilbert空间中[6-7].本文主要利用算子理论的基本知识，在无限维Hilbert空间中,给出一类算子方程：

X-s+A*XtA=B(A,B∈B(H),B>0)

(1)

正算子解的一些性质.

1 预备知识

设Hilbert空间H是复可分的，其上有界线性算子的全体记为B(H).A是B(H)上任意给定的一个算子，σ(A)、A*、r(A)表示算子A的谱、伴随算子、谱半径. (·,·)与‖·‖分别表示Hilbert空间中的内积和范数.

定义1设A∈B(H)，对于∀x∈H，如果满足(Ax,x)≥0，则称A为正算子，记为A≥0；显然，正算子A满足A≤‖A‖I；若A>0，称A为可逆的正算子，显然，当A≥B>0时，A-1≤B-1.

定义2设A∈B(H)，如果满足A*=A，称A是自伴算子.

定义3设A∈B(H)，称σ(A)=sup{λ∈C,A-λI不可逆}为算子A的谱.

引理1[1]设A∈B(H)，且A是一个正规算子，则有ω(A)=r(A)=‖A‖.

引理2[1]设P、Q是正算子，且P>Q，如果PQ=QP，则对∀t>1有Pt>Qt成立.

引理3[2]设A、B为B(H)上的两个自伴算子，且A≤B，则对∀T∈B(H)满足T*AT≤T*BT；对于任意给定的正算子A、P，下列结论显然成立：

(H1)A可逆，则对于∀t>0,t∈R，满足‖At‖=‖A‖t.

(H2)P可逆，记λmax(P)=max{λ:λ∈σ(P)}，λmin(P)=min{λ:λ∈σ(P)}，有λmin(P)I≤P≤λmax(P)I.

2 主要结论及证明

证明 由方程知X-s=B-A*XtA≤B≤‖B‖I，故

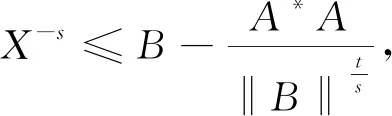
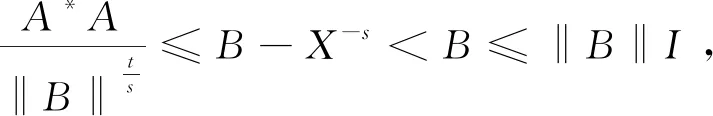
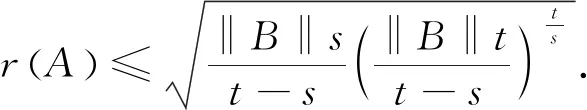
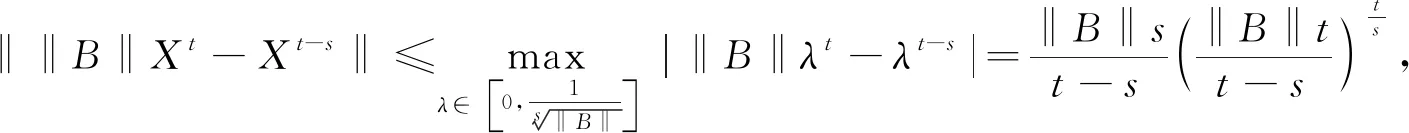
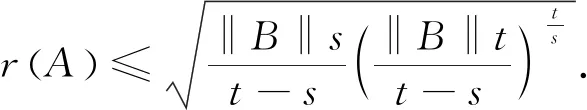
若X是方程的正算子解，则由方程知X-s=B-A*XtA≤B=α0B,设X-s≤αkB，下证X-s≤αk+1B.因为：

所以，对于一切n∈N有X-s≤αk+1B成立.

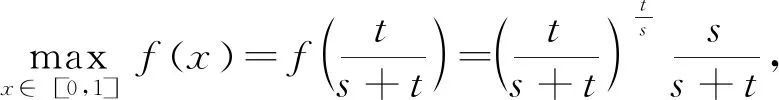
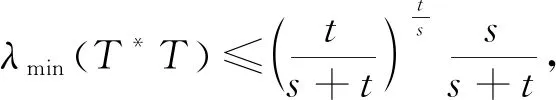
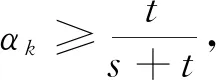
定理4如果算子方程(1)有正算子解，则下列两个结论成立：

证明 (1)因为0

0<λmin(X-s)I≤X-s≤λmax(X-s)I,

0<λmin(B)I≤B≤λmax(B)I,

且

λmax(X-s)≤λmax(B),

故