金兹堡-朗道方程组的整体吸引子

刘 帅，陈淑红

（闽南师范大学数学与统计学院，福建漳州363000）

整体吸引子是无穷维动力系统研究的重要内容，对于揭示系统解的长时间行为具有重要的意义.本文主要研究BEC - BCS跨越模型在有外力作用时，所得到的依赖于时间t的金兹堡-朗道方程组整体吸引子的存在性.

Henry[1],Roger[2]对金兹堡-朗道理论及整体吸引子的研究取得了长足的进步.Schakel[3]利用导数展开法从微观BCS模型中推导出具有时间依赖性的金兹堡-朗道理论；Drechsler等[4]推导出金兹堡-朗道理论去描述BCS 超导性与玻色凝聚的跨越；Machid 等[5]研究了BEC - BCS 跨越附近原子费米子气体的具有时间依赖性的金兹堡-朗道方程，证明了除BEC 限制外，具有时间依赖性的金兹堡-朗道方程的GL 系数是复数.Ghidaglia 等[6]和Promislow[7]在1 维和2 维空间研究了带立方非线性项的金兹堡-朗道方程的有限维整体吸引子；郭柏灵[8]研究了广义Kuramoto-Sivashinsky 型方程周期初值问题的整体吸引子；Sell[9]研究了3维Navier-Stokes 方程整体吸引子的存在性；戴正德[10]研究了耗散KDV 型方程Cauchy 问题的动力学行为及整体吸引子的存在性.

基于以上的研究，本文致力于BEC - BCS跨越中带外力项的金兹堡-朗道方程组的整体吸引子，并得到了以下结果.

1 引理

引理1[1]令1 ＜p ＜∞，若对于任意的u ∈C2()满足

则有

通常地，n表示边界∂Ω的外法向量.

由式(5)，可以推出

引理2[2]令E 是一个巴拿赫空间，{St,t ≥0}是一个半群算子，St:E →E，满足St⋅Sτ= St+τ，S0= I，这里I是一个恒等算子，且假定算子半群St满足如下条件：

1)算子St在E 上是一致有界的，即对于任意的R ≥0，存在一个常数C(R)，使得当||u⇀||E≤R 时，对于任意的t ∈[0,∞)，有||Stu⇀||E≤C(R);

2) 存在一个E 上的有界吸收集B0，即对于任意的有界集B ⊂E，存在一个常数T，使得当t ≥T 时，有StB ⊂B0;

3)当t ＞0时，St是一个全连续算子；

则算子半群St有一个紧整体吸引子.

2 先验估计

为了证明定理1，先对弱解Δ(x,t)和φB(x,t)建立适当的先验估计.

其中

证明式(1)-(2)可以转化为

其中

由引理1，

其中

因为

3 整体吸引子的存在性

为了得到方程组(1)-(4)整体吸引子的存在性，我们需要证明定理1.

证明 取巴拿赫空间E = H1,2(Ω)×H1,2(Ω)，设=(Δ(x,t),φB(x,t))T是式(1)-(4)的弱解，做映射St:St(x,t)=(x,t)为E →E 的映射，且S0= S0(x,0)= u⇀(x,0)，则St是由式(1)-(4)生成的半群算子.下面逐条验证引理2的条件.

利用定理2、定理3的结论，可见对以R为半径的球BR⊂E，取B ⊂BR，则

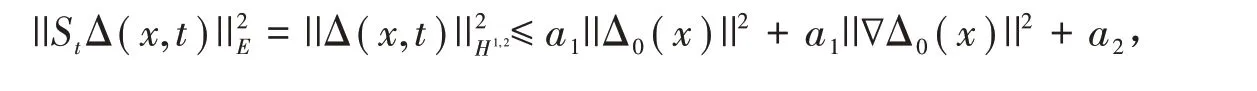
此处a1，a2是正常数.

故St在E上是一致有界的.

由定理2、定理3的结论可得

其中A1,A2,||φB0(x)||2,||∇φB0(x)||2全为有界常数.

取D = max{A1,A2,||φB0(x)||2,||∇φB0(x)||2}，可得

由定理4得，当t ＞0时，

其中K为有界常数.因此St是一个全连续算子.