函数的合成与分解
鲁 彬
(江苏省姜堰第二中学,225500)
《普通高中数学课程标准(2017年级)》要求:“高中数学课程内容突出函数、几何与代数、概率与统计、数学建模活动与数学探究活动四条主线,它们贯穿必修、选择性必修和选修课程”.由此可见,函数在高中数学中占有重要地位,同时也是高考考查的重要内容.高考中的函数内容丰富,考点众多,题型多变,对学生综合运用数学知识和思维能力提出很高的要求.笔者通过研究,发现在一类函数与不等式(或者方程)结合的试题中,把目标函数进行恰当地变形并分解为几个子函数,根据需要逐个研究子函数的相关性质,往往能够化繁为简.下面通过几道例题与大家分享与交流.
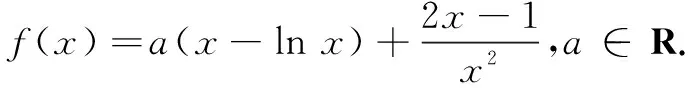
(1)略;
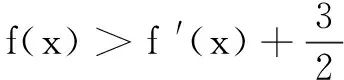


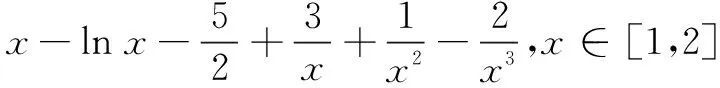
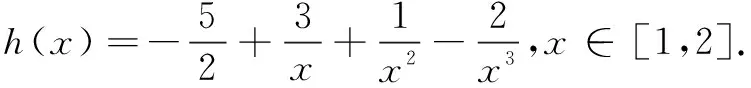
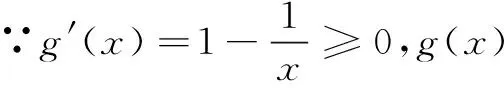
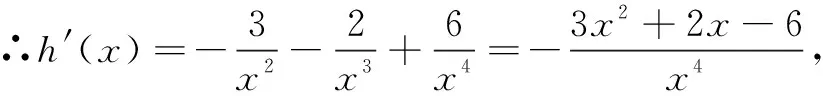
当x∈(1,x0)时,h′(x)>0;当x∈(x0,2)时,h′(x)<0.
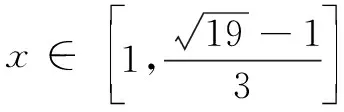

又因为x不可能同时取到1,2,
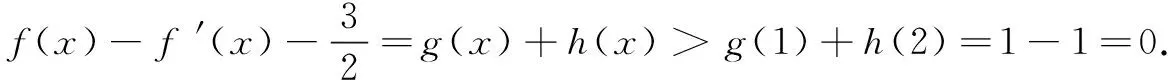
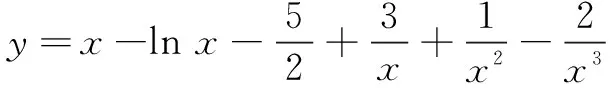

(1)(2)略;
(3)设g(x)=(x2+x)f′(x),其中f′(x)是f(x)的导函数.证明:对任意x>0,g(x)<1+e-2.
证明(3)由(1)得k=1,
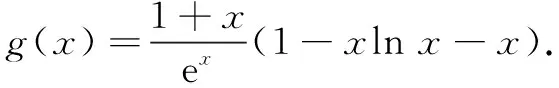

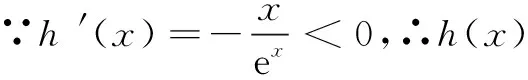
② ∵φ′(x)=-lnx-2,令φ′(x)=0,得x=e-2.当x∈(0,e-2)时,φ′(x)>0,φ(x)在(0,e-2)上单调递增;当x∈(e-2,+∞)时,φ′(x)<0,φ(x)在(e-2,+∞)上单调递减.故φ(x)≤φ(e-2),即1-xlnx-x≤1+e-2.
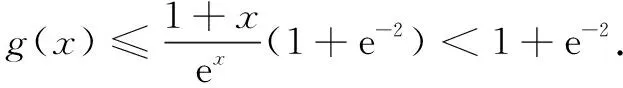
评注本题把g(x)分解成两个子函数h(x),φ(x)的积,分别研究h(x),φ(x)的取值范围得到:h(x)<1,且φ(x)≤1+e-2.结合h(x)>0以及不等式的性质,可得
g(x)=h(x)·φ(x)≤h(x)·(1+e-2)<1·(1+e-2)=1+e-2.若由h(x)<1且φ(x)≤1+e-2直接得到h(x)·φ(x)<1·(1+e-2)=1+e-2,这显然是错误的.因此两个不等式相乘时应正确运用不等式的性质.

(1) 略;
(2)证明:f(x)>1.
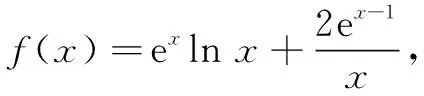
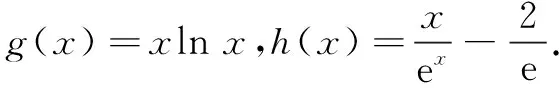

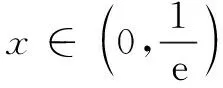
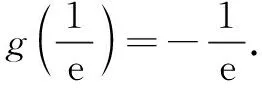
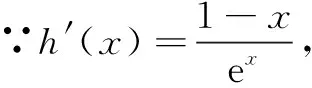
所以当x∈(0,1)时,h′(x)>0;当x∈(1,+∞)时,h′(x)<0.
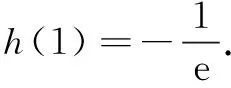
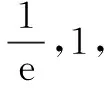
评注(1)一般地,若要证F(x)≥0,移项得f1(x)≤f2(x),通过介值λ,使得f1(x)≤λ≤f2(x)成立即可.这个介值通常与两个子函数的最值有关,有时也会涉及两个介值λ1,λ2,使得f1(x)≤λ1≤λ2≤f2(x)成立.(2)另一种情况,通过中间函数φ(x),使得f1(x)≤φ(x)≤f2(x)成立即可,这个中间函数φ(x)可取y=f1(x),y=f2(x)的公切线对应的函数解析式.
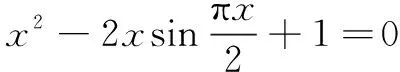
解显然x=0不是方程的解.


易知f(x)和g(x)都是奇函数,其中x∈(-∞,0)∪(0,+∞),故只需研究x∈(0,+∞)的部分.



故方程的解需满足x=1且x=4k+1,k∈N,即x=1.
由对称性,可知x=-1也是方程的解.
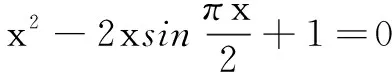
评注本题把方程变形并分解为两个子函数f(x)和g(x),分别研究两个函数f(x)和g(x)的最值,得到1≤f(x)=g(x)≤1.由夹逼准则,可知f(x)=g(x)=1,且等号成立时x取值的交集即为所求.

