基于跳扩散模型的DC型养老金时间一致最优投资策略的研究

付渴 曹静

摘 要 将养老金投资过程分成财富积累阶段和财富给付阶段，建立了DC型养老金在退休前和退休后个人账户积累额变动的连续时间随机模型. 该模型考虑了工资的随机风险因素，并用跳扩散模型刻画风险资产. 以均值方差准则作为优化目标，运用推广的 HJB方程分别得到了退休前和退休后的时间一致最优风险资产投资最优解. 最后通过算例及敏感性分析研究了各个因素对风险资产投资的影响. 在这些因素中缴费比例、死亡力对风险资产投资比例均有负向影响.

关键词 金融学;最优投资策略;二次规划;DC型养老金;跳扩散模型;随机工资

中图分类号 F840.67           文献标识码 A

Abstract The pension investment process is divided into two stages： the wealth accumulation stage and the wealth payment stage. Continuous time stochastic models of the amount of DC pension accumulation in individual accounts before and after retirement are established. The models consider the stochastic risk factors of wages and jump-diffusion model is used to portray risky assets. Taking the mean-variance criterion as the optimization objective， the optimal solution of venture capital investment before and after retirement was obtained by using the generalized HJB equation. Finally， through numerical examples and sensitivity analysis， the influences of various factors on venture capital investment are analyzed. Among these factors， contribution ratio and death force have negative influences on the proportion of venture capital investment.

Key words finance;optimal investment strategy;quadratic programming;DC pension plan; jump-diffusion model;stochastic salary

1 引 言

养老金是老年社会保障制度的重要组成部分，根据贡献和收益的不同设置，养老金主要有两种类型：固定收益型（DB： defined benefit）和固定缴款型（DC： defined contribution）. 在DB型养老金中，退休后的收益由保险公司预先确定，而工作期间的缴款额根据养老基金的价值进行调整. 在该计划中保险公司承担了可能发生的各种风险，例如投资风险、养老金计划成员寿命风险等. 近年来，随着人口结构的变化和死亡率的下降，DB型养老金面临着向退休人员给付规定收益的巨大压力. 而在DC型计划中，缴款额是预先确定的常数或养老金计划成员收入的固定比例，收益则取决于退休前缴款额的积累及该养老基金投资组合的回报. 如今，随着金融市场的快速发展和人口死亡率的降低，许多国家的养老金计划都是基于DC型也即固定缴款型计划的.

现有文献中，关于DC型养老金计划模型的优化目标主要有3种. 第一种是最大化终端财富效用，收益性是此类优化目标关注的重点. 常浩等（2018）[1]将终端财富的效用分别用幂效用函数和指数效用函数来描述，并对比和分析了这两种效用函数对DC型养老金最优投资策略的影响. Chen等（2017）[2]考虑的是最大化终端财富与最低退休工资差值的S型效用函数. 第二种是动态最小化养老基金账户与预定投资目标之间的预期二次损失，该类优化目标更加关注投资的安全性，为参保人提供了稳健的养老金给付. 何林和梁宗霞（2016a）[3] 将积累期结束时实际与预期累积额的二次偏差的最小化作为优化控制目标，为了描述参保人对正向偏差的偏好和负向偏差的厌恶，在目标函数中加入了一个负的一次偏差项. 第三种是在养老金的管理中应用均值方差准则，此类优化目标兼顾了收益与风险的平衡，更加符合养老金管理的要求. Bjrk等（2014）[4]考虑的均值-方差准则中其风险规避系数是状态依赖的，并在该准则下得到最优投资策略，由于方差缺乏迭代期望性质，多周期或连续时间框架下动态MV准则下的最优投资问题不满足Bellman最优性原理，因此模型最优解是时间不一致的，需要采用推广的HJB方程来求解这样的时间不一致问题.

在对风险资产价格过程的假设中，最早的文献大都是基于风险资产的价格过程满足几何布朗运动的假设下进行的. 肖建武等（2006）[5]考慮到风险资产价格过程的常方差弹性（CEV）模型，并在最大化指数效用的条件下采用Legendre 变换将原问题转化为对偶问题进行求解得到最优策略. Sun等（2016）[6]考虑到金融市场中风险资产的价格会出现大起大落式的跳跃情况，便用跳-扩散模型来刻画风险资产价格过程，此类信息到达的时间及造成的冲击影响均是随机的，可以利用泊松过程予以数学描述.

在影响养老金财富积累的因素选择上，Sun等（2016）[6]考虑了保费返款条例，其风险规避系数是状态依赖的. Bian等（2018）[7]考虑了体制转换模型. 孙惠玲等（2015）[8]考虑了通货膨胀、市场利率的Vasicek模型. 何林和梁宗霞（2016）[9]考虑了生命周期、风险偏好和累计水平对资产配置策略的影响. 杨鹏（2018）[10]主要研究的是Vasicek模型的随机微分博弈. 高建伟和乌云高（2018）[11]在不确定理论下研究最优投资策略问题. 何林和梁宗霞（2006）[2]考虑了工资变动及其工资替代率. 伍慧玲和董洪斌（2016）[12]考虑了通胀风险及随机收入等因素. 考虑到DC型养老金的投资期间一般长达几十年，养老金参保人的工资水平大多都是随机波动的，所以考虑随机工资是非常有必要的.

参考张初兵和荣喜民（2012）[13]对整个养老金投资阶段的划分，考虑了退休前和退休后的两个阶段，分别为财富积累阶段和给付阶段. Li和Rong（2016）[14]在养老金计划中对随机工资的刻画可资借鉴. 同时假设了风险资产服从跳扩散模型，给出了时间一致最优风险资产投资最优解. 最后给出了算例，更直观地分析各因素对整个投资计划的影响，增加了对研究的有效性和可操作性的验证.

2 均值方差下时间一致最优化模型的建立

由图3可知风险资产的最优投资比例会随着缴费比例的增加而减少的. 可以观察到，在刚开始的时候，缴费比例对风险资产的最优投资比例所造成的影响并不显著，而通过数十年的积累效应，这种影响程度越来越大. 对于缴费比例较少的参保人，为保证退休后有足够的养老金给付，需要将相对较多的钱投放风险资产中以获取更多利益.

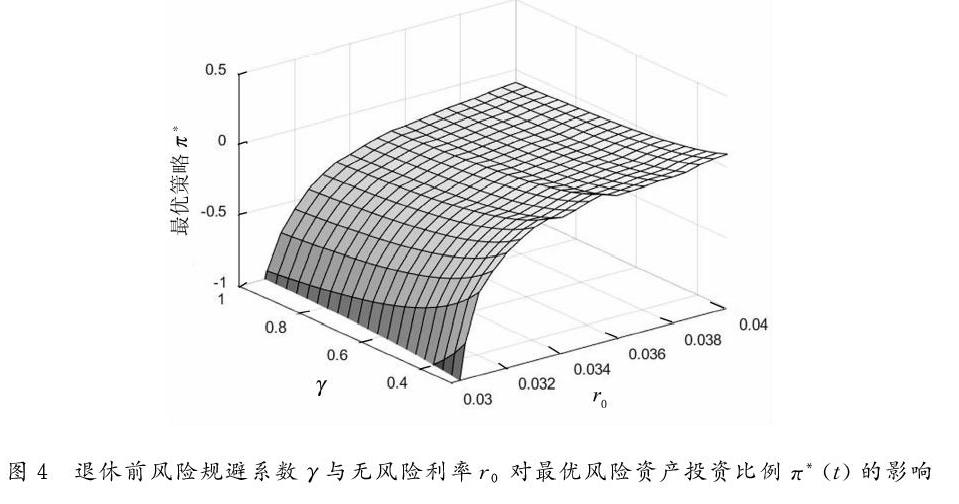
风险规避系数描述了投资人对风险的规避的程度，图4给出了风险规避系数γ与无风险利率r0对最优风险资产投资比例π*（t）的影响. 退休前，财富过程处于积累阶段，风险规避程度越大越会影响投放在风险资产中的比例. 但随着无风险利率的增加，最优风险资产投资比例并不会因此而减少，但会更加谨慎地选择其投放比例，也即增加的幅度会变缓. 因为此时无风险利率所带来的收益依然远不如风险利率，所以依然会增加投放在风险市场中的比例，但考虑到安全性，会缓慢的增加该投放比例.

2）退休后（给付阶段）

图5显示了最优风险资产投资比例π*（t）随时间的变化规律.很明显地观察到最优资产策略随时间呈负相关关系. 可以解释为，刚退休时，财富积累值达到最大，为了保证后期有足够的财富给付，此时需要将相对较大比例的财富积累投放在风险市场中以获得更大的利润.而随着时间增加，不断的定期给付养老金，整个财富积累不断减少，为安全起见需要减少投放在风险资产上的比例来降低风险.

死亡力描述了一段时间内某一特定年龄的死亡概率，在这里假设死亡力为定值，由图6可知死亡力对最优风险资产投资比例有负向影响. 这是因为随着死亡力的降低也即死亡人数的降低，需要给付的养老金就会越多，为了保证能够有足够的财富作为养老金定期给付给生存者就需要增加投资于风险资产的比例以此获取更大的利益.

图7（a）和图7（b）分别给出了风险规避系数γ与无风险利率r0对最优风险资产投资比例π*（t）和最优值函数V的影响. 退休后，当无风险利率r0增加时，无风险资产更具有吸引力，因此投资人将会把更多的资产投放到无风险市场中从而减少持有风险资产的比例. 而风险规避程度越大，投资人将财富投放到风险市场中的比例越小以此来规避风险.注意到当无风险利率和风险规避系数均增加时最优值也会增加，说明在合适的时候适当的增加无风险资产的比例会增加最优值.

μz和λ分别代表风险资产的价格平均跳幅与风险资产价格跳的强度，图8（a）和图8（b）分别描述了这两个因素对风险投资资产比例和最优值函数的影响. 当风险资产的价格平均跳幅μz增加时，最优风险资产投资比例会减少来避免风险，而当风险资产价格跳的强度λ增加时该比例会增加来获取更大利益，当两者同时增加时，风险资产投资比例整体呈上升趋势，说明投资人会增加在风险资产上的投资份额，但投资是理性的. 同时，随着平均跳幅和强度的增加，最优值也会不断增加，体现了风险越大，收益越大的特点.

5 结 论

研究了具有跳-扩散价格模型和随机工资的DC型养老金的最优投资问题，将投资过程分成了财富积累阶段和财富给付阶段，分别对应退休前和退休后.首先，介绍了目前养老金管理的现状以及发展趋势，并结合实际情况说明了研究DC型养老金的必要性，根据目前国内外对DC型养老金问题研究的进展，重点关注了时间一致框架下DC养老金投资和给付问题的研究及求解.其次，基于现有研究，假定风险资产服从跳扩散模型，考虑了随机工资的影响，分别给出了退休前和退休后的财富积累过程和投资优化目标，建立了广义的HJB方程来解决时间不一致问题，得到最优投资策略和有效前沿.最后，通过数值模拟，分析了缴费比例、死亡力等参数对最优投资策略和最优值函数的影响，并从实际生活的角度对其进行了合理解释.

参考文献

[1] 常浩，王春峰，房振明. 随机利率与随机波动率环境下的DC型养老金计划[J]. 控制与决策，2019，34（3）：581-590.

[2] CHEN Z，LI Z F，ZENG Y，SUN J Y.Asset allocation under loss aversion and minimum performance constraint in a DC pension plan with inflation risk[J]. Insurance： Mathematics and Economics， 2017，75：137-150.

[3] 何林，梁宗霞. DC型養老金积累期最优资产配置问题研究[J]. 保险研究， 2016（6）：102-111.

[4] BJRK T，MURGOCI A，ZHOU X Y. Mean-variance portfolio optimization with state-dependent risk aversion[J]. Mathematical Finance，2014，24 （1）：1-24.

[5] 肖建武，尹少華，秦成林. 养老基金投资组合的常方差弹性（CEV）模型和解析决策[J]. 应用数学和力学，2006，27（11）：1312-1318.

[6] SUN J Y，LI Z F， ZENG Y. Precommitment and equilibrium investment strategies for defined contribution pension plans under a jump-diffusion model[J]. Insurance： Mathematics and Economics，2016，67：158-172.

[7] BIAN L H，LI Z F，YAO H X. Pre-commitment and equilibrium investment strategies for the DC pension plan with regime switching and a return of premiums clause[J]. Insurance： Mathematics and Economics，2018，81：78-94.

[8] 孙惠玲，王传玉，房冬冬. 考虑通胀和随机利率的 DC 型养老金计划最优投资问题研究[J]. 延安大学学报：自然科学版，2015，34（4）：21-26.

[9] 何林，梁宗霞. 生命周期、风险偏好和积累水平对DC型养老金资产配置策略的研究影响[J]. 经济理论与经济管理，2016（4）：25-33.

[10]杨鹏. 随机利率下DC型养老金的随机微分博弈[J]. 应用概率统计，2018，34（5）：441-449.

[11]高建伟，乌云高. 不确定理论下的DC型养老金的最优投资策略问题[J]. 数学的实践与认识，2018，48（4）：97-106.

[12]伍慧玲，董洪斌. 带有通胀风险和随机收入的确定缴费养老计划[J]. 系统工程理论与实践，2016，36（3）：545-558.

[13]张初兵，荣喜民. 均值方差模型下DC型养老金的随机最优控制[J]. 系统工程理论与实践，2012，32（6）：1314-1323.

[14] LI D P，RONG X M，ZHAO H. Time-consistent investment strategy for DC pension plan with stochastic salary under CEV    model[J]. Journal of Systems Science & Complexity ，2016，29（2）：428-454.

[15]HE L，LIANG Z X. Optimal dynamic asset allocation strategy for ELA scheme of DC pension plan during the distribution phase[J]. Insurance： Mathematics and Economics，2013，52（2）：404-410.

[16]BJRK  T，MURGOCI A. A general theory of markovian time inconsistent stochastic control problems[J]. Ssrn Electronic Journal，2010，18（3）：545-592.