一类具有随机扰动的SIQR模型的灭绝性

刘 娟

（蚌埠学院，安徽 蚌埠233030）

0 引言

近年来传染病模型受到了国内外学者的广泛关注，成为生物数学模型中重要的一类模型。利用微分方程理论研究传染病模型可以说明传染病的传播特性，能实现对传染病的预防与控制。目前对确定型传染病模型研究得较多，许多有意义的结果被得出［1-6］。但是在现实的环境中，随机干扰无处不在，随机因素对传染病的爆发有重要的影响，因此，在确定型模型中加入随机扰动项是很有必要的。文献［7］研究了下列具有时滞项的传染病模型：

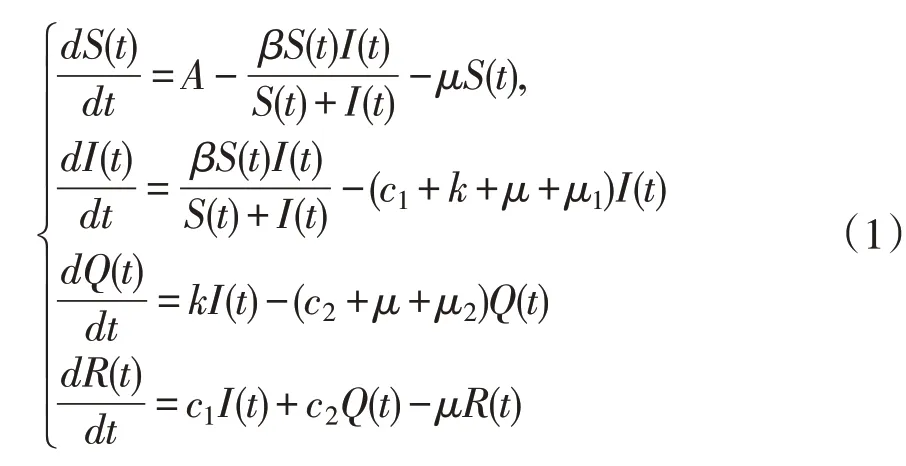
（1）式中S(t)、I(t)、Q(t)、R(t)分别表示易感者、染病者、隔离者、治愈者在时刻t的数量［8-10］。 A 表示人口的常数输入率，μ为人口的自然死亡率，假设易感者、染病者、隔离者具有相同的死亡率，μ1，μ2表示染病者、隔离者的因病死亡率，c1，c2和k均为系统的状态转移率为感染率函数。文献［7］研究了模型（1）Hopf分支的存在性。

对于某些传染病而言，确定型模型是无法全面描述其传染规律的，模型（1）并未考虑到疾病传播过程中存在的白噪声，而白噪声可以引起系统稳定性发生变化，甚至导致系统中的某一群体灭绝。因此考虑到白噪声的影响，本文在模型（1）中引入随机扰动项。假设外界白噪声主要影响参数为β，即βdt→βdt+σdB(t) ，B(t) 为 标 准 的 布 朗 运 动 且B(0)=0，σ2为白噪声强度，这样可以得到传染病系统（2）。本文将研究随机传染病模型（2）正解的存在唯一性及疾病何时消失。

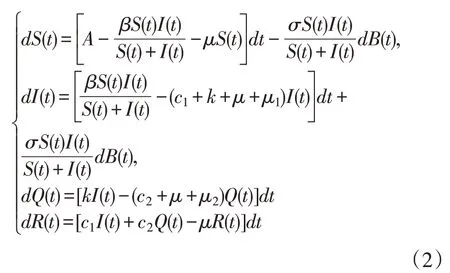
1 系统正解的存在及唯一性

定理1 任意给定的初始条件X(0)=(S(0)，I(0)，Q(0)，R(0))，系统（2）存在唯一的解，且该解以概率1 存在于中，即系统（2）存在唯一的全局正解。

证明 设I=ev(t)，即v(t)=lnI，利用Itô公式有

则将系统（2）变为

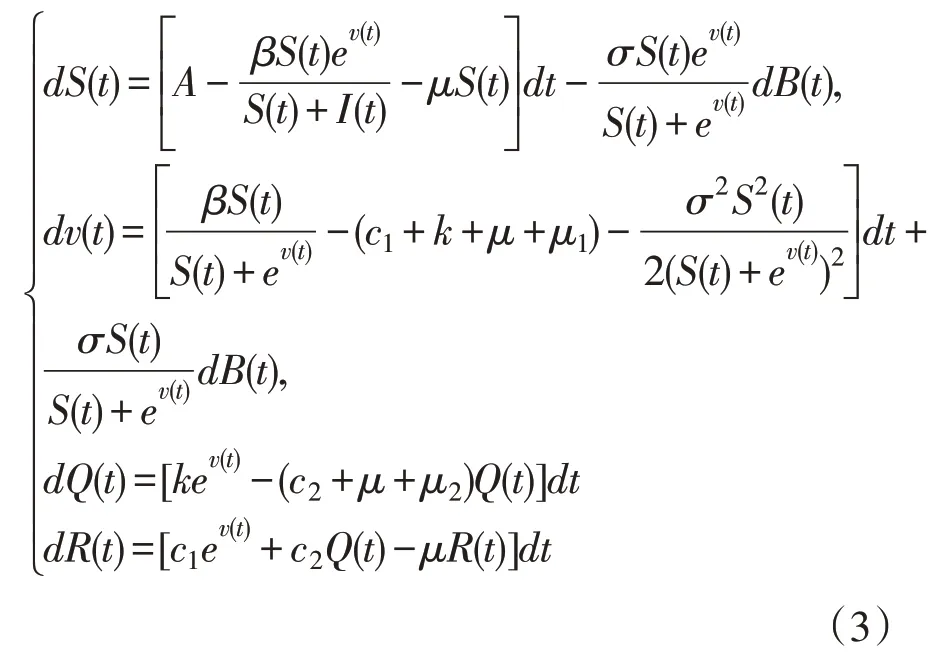
易知系统（3）与系统（2）等价，且系统（3）满足局部利普希茨条件，则对任意的初始条件，系统（3）存在有唯一的局部解X(t)(t∈[0，τe])，其中τe是系统的爆破时间。以下证明X(t) (t∈[0，τe])是系统（2）的全局正解，只要证明τe=∞a.s.，就可得该结论。

设k0≥1，能使(S(0)，I(0)，Q(0)，R(0))都位于区间中，再设k≥k0，设停时

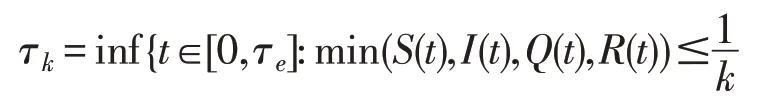
或max(S(t)，I(t)，Q(t)，R(t))≥k}

规定inf ∅=∞，由停时定义知τk是k的单调增函数，设如能证明τ∞=∞，则τe=∞且X(t) ∈(t≥0)。所以利用反证的思想证明τ∞=∞，假设τ∞≠∞，则存在常数T 及ε∈(0，1)，有

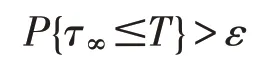
成立，故存在k1≥k0，使得对所有的k≥k1，有

对于系统（2），将等式两边相加得

对于d(S+I+Q+R)=[A-μ(S+I+Q+R)]dt

利用初值X(0)=(S(0)，I(0)，Q(0)，R(0)) ，可求得

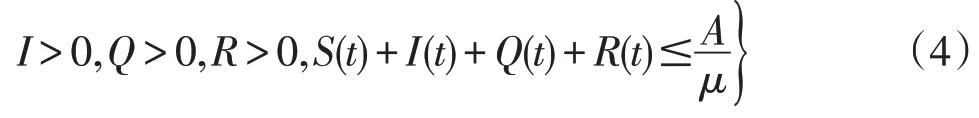
为系统（2）的正不变集。

定义

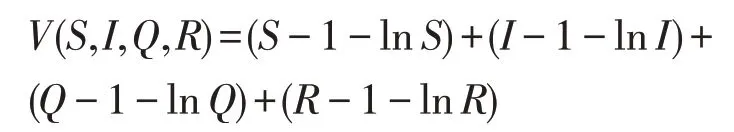
令T＞0，则对任意t:0 ≤t≤τkT，利用Itô公式有

令

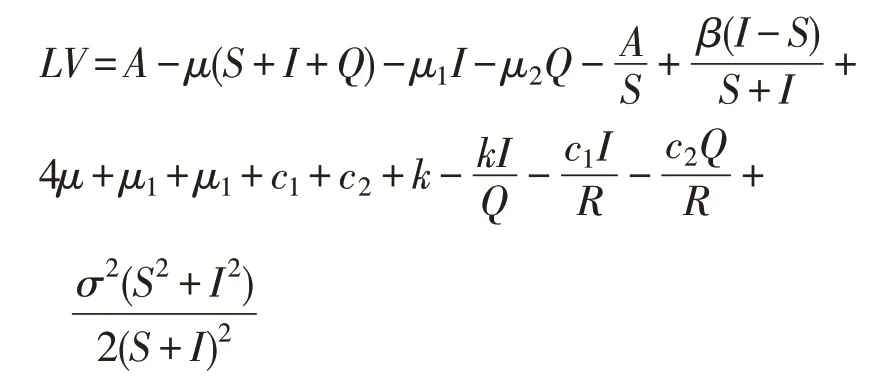
则

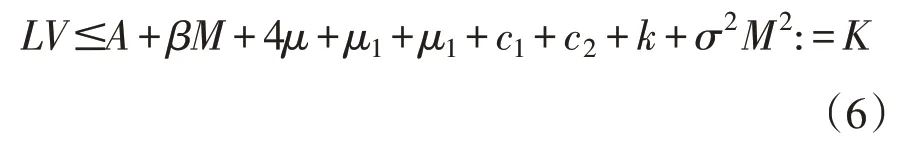
将（6）式代入（5）式得

对（7）两边取0到τkT的积分，再取期望得

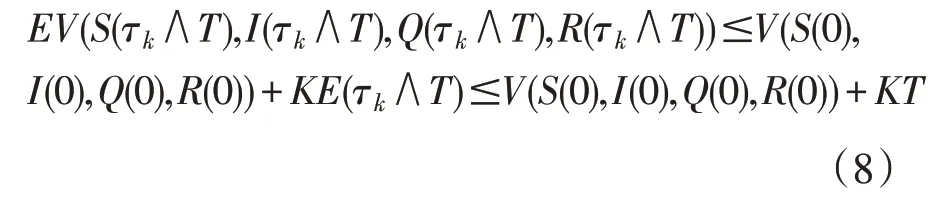
对所有的k≥k1，有P{τk≤T}＞ε。而对每个ω∈{τk≤T}，S(τk,ω)，I(τk，ω)，Q(τk，ω)，R(τk，ω)这四个量中至少有一个等于k或，则

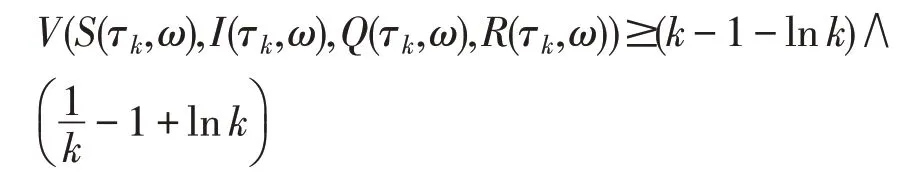
由（8）得

其中Ωk={τk≤T}，1Ωk(ω)为Ωk的示性函数，令k→∞，得

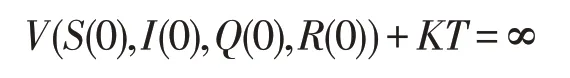
矛盾，故假设不成立，由此证明了τe=∞a.s.，则系统（2）存在唯一的全局正解。

2 系统疾病的灭绝性

以下讨论系统（2）中疾病的灭绝条件，对于疾病何时消失，有如下的定理。

定理2 设X(t)=(S(t)，I(t)，Q(t)，R(t)) 为系统（2）的解，对于任意初始条件X(0)∈Γ∗，若

则

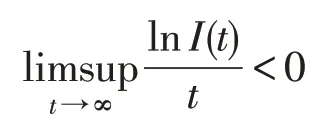
证明 利用Itô公式，将系统（2）中的第二项变为

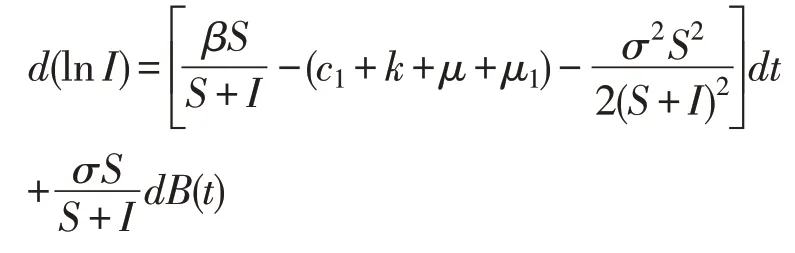
将上式两边取0到t的积分，再除以t，得

即得

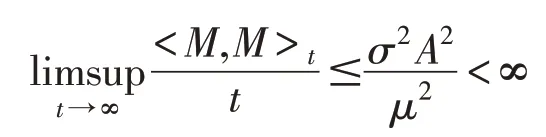
由强大数定律得在（9）式两边取上极限，并将（10）式代入（9）式得

3 结论

本文在文献［7］基础上，讨论了一类具有随机扰动的SIQR模型的正解存在性及疾病的灭绝性，定理2的结果表明，在满足一定条件的前提下，若能使白噪声强度足够大，则疾病I（t）几乎处处指数趋于0，即疾病将灭绝，几乎消失。定理说明了外界白噪声对传染病系统的影响，具有一定的生物学意义。