无源对流扩散方程的两类修正差分格式

王彩华,杜金月,张静

(天津师范大学数学科学学院,天津300387)

1.引言

界点集Γ=Γh={x0,xN}.记结点集对应的下标集ω={i|i=1,2,··· ,N−1},γ={0,N},.

本文中u(x0),u(x1),··· ,u(xN)为方程(1.1)在剖分结点处的精确值,简写为u0,u1,··· ,uN.U0,U1,··· ,UN为数值方法在结点处的近似值.A(xi)简记为Ai,记Pe(x) =A(x)h/ε,Pei=.

因本文在数值实验部分选取了多种差分格式进行了综合数值比对,这里先将相关参考文献中的差分格式(简记为FD1,FD2,...,FD7)及实验结果简介如下.

基于模型方程(1.1),文[3]首先给出一种差分格式FD1,该格式具有二阶精度和无条件稳定收敛性,能够突破中心差分格式µ ≤2的限制,实验表明此格式适合数值求解参数ε较大的对流扩散问题,但当ε减小时FD1 数值精度下降.根据对流扩散过程的迎风效应,文[3]继续将FD1修改成具有二阶精度、无条件收敛的差分格式FD2;进一步地,文[3]在FD2基础上通过摄动处理,建立了具有四阶精度的差分格式FD3.实验表明差分格式FD2,FD3适合求解ε较小的问题,但当网格过密部分结点位于边界层附近时数值解精度变差.

Dennis等人提出了四阶差分格式FD4[4],但数值实验表明仅当ε较大时数值精度较好.陈国谦在二阶指数型的Il’in[6]格式基础上,通过对系数进行二阶摄动修正,得到新的差分格式FD5[5],此差分格式具有四阶精度,针对无源对流扩散问题数值计算效果较好.但文[7]指出FD5求解含源问题时数值精度下降.

文[7]通过对微分方程系数常数化处理与余项修正的思想,给出变系数的对流扩散方程的四阶指数型差分格式FD6[7],FD6与FD5针对无源问题数值计算效果相当,FD6亦适宜于求解含源问题.

文[8]给出具有四阶精度的FOC差分格式,但此格式色散误差和耗散误差较大.基于截断误差余项修正思想,文[9]在FOC基础上给出一种有理型的四阶紧致差分格式FD7[9],实验结果表明该差分格式在ε较大时计算效果较好,却不适应小参数问题.

综上可见,有些参考文献所给出的差分格式适合求解参数ε较大时的对流扩散问题,而有些格式适合求解参数ε较小时的问题.本文考虑能否在设计差分格式时即可根据ε的大小灵活选择合适的差分格式,且数值计算精度更高,为此设计了两类差分格式: 一类是横向系列差分格式,适用于求解ε较大时的对流扩散问题,通过修正方法可使得该系列格式达到二阶、四阶、六阶、八阶数值精度,且第5节实验表明当参数较大时本文的高阶差分格式数值精度优于各种参考差分格式;另一类是纵向系列格式,适用于求解ε较小时的对流扩散问题,实验表明随着参数ε的减小,横向系列格式数值计算精度逐渐变差,而纵向系列格式数值精度逐渐提高,且亦优于参考格式.

本文将横向系列修正差分格式简记为HDS1(同中心差分格式CDS),HDS2,HDS3,HDS4等(HDS:Horizontal Difference Scheme);将纵向修正的系列差分格式简记为VDS1(同Il’in格式),VDS2,VDS3等(VDS: Vertical Difference Scheme).

2.横向与纵向系列修正差分格式的设计思路

设函数u(x)充分光滑,当i=1,2,··· ,N−1时,将ui+1、ui−1在点xi处进行Taylor展开

如设

显然q1(x)=1.对上式两边求导,有

得到递推公式

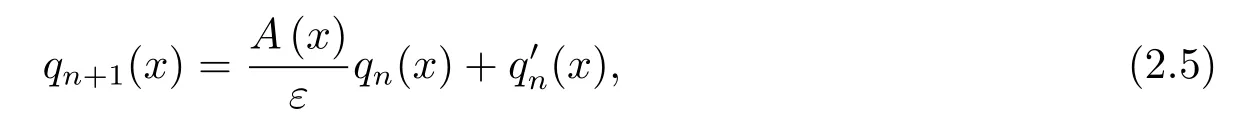
依据上面递推公式,可列出u(x)的高阶导数降阶组式如下

横向系列差分格式的设计思路: 当ε较大时(例如为1时),将上面降阶组式(2.6)代入泰勒展式(2.1),(2.2),可见,(2.1),(2.2)中h幂次保留几项将对数值精度影响较大.如式(2.1),(2.2) 只保留到u′′(x)项,且将组式(2.6) 的的表达式代入到式(2.1),(2.2),两式联立消去u′(x)即可得到二阶差分格式HDS1(同经典的中心差分格式CDS);在HDS1基础上继续修正,(2.1),(2.2)保留到u(3)(x),u(4)(x),组式(2.6)相应的降阶式子代入式(2.1),(2.2),消去u′(x),则得到四阶差分格式HDS2;继续修正,展式(2.1),(2.2)保留到u(5)(x),u(6)(x) 可得到六阶差分格式HDS3;展式(2.1),(2.2)保留到u(7)(x),u(8)(x),可得到八阶差分格式HDS4.这一过程可以继续下去,本文仅详细给出了HDS1-HDS4的差分格式.

纵向系列差分格式是在文[13]基础上的改进,设计思路为: 当ε较小时(ε <<1),由降阶组式(2.6)可见ε的负指数幂次如何保留对数值格式精度影响远超过h的作用,此时上面的横向差分格式设计不适宜求解小参数问题,本文设计了纵向差分格式.如组式(2.6) 仅保留纵向第一列关于1/ε指数幂次最大的项,舍去其他项,将其代入(2.1),(2.2),得到的关于u′(x) 的系数是收敛级数,联立(2.1),(2.2)消去u′(x)即得到的纵向差分格式VDS1(同Il’in格式);在VDS1 基础上继续修正,保留1/ε指数幂次下一项即次大的项,整理可得差分格式VDS2;同理进一步修正可得VDS3.这一过程可以继续下去,本文仅给出了VDS1-VDS3 的差分格式.在纵向系列差分格式设计中,组式(2.6)中因为对u′′(x),u(3)(x)...都取了部分项作为近似代入(2.1),(2.2）,这与常见差分格式构造思路不同，不能也不必进行关于h的截断误差分析.

接下来具体给出横向系列差分格式与纵向系列差分格式.

3.横向系列修正差分格式

为简便记u(k)(xi)为u(k)i,联立式(2.1)和(2.2),且由降阶组式(2.6)可知,当i=1,2,··· ,N−1时

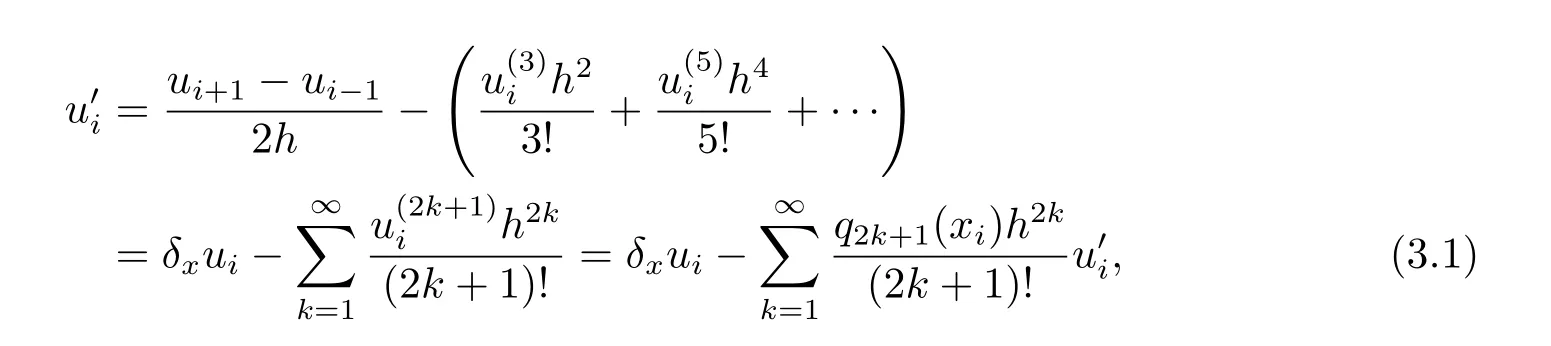
其中

其中ξi7,ξi8∈(xi−1,xi+1).

同前面格式推导过程一样地,整理式(3.31)可得

4.纵向系列修正差分格式

由式(2.1),(2.2)及组式(2.6)得

此格式记为VDS2.

Ⅲ纵向差分格式VDS3

观察组式(2.6)中qk(k=1,2,···),在VDS2基础上,如保留分母中关于ε相同幂次的第三列和第四列,即保留qk的前四列,其通项分别为

5.数值实验

例5.1对流扩散问题{

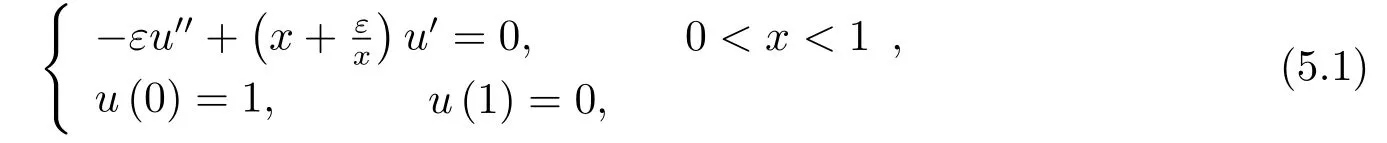
精确解

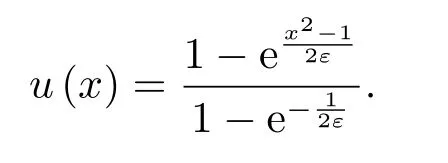
图5.1 参数不同时算例5.1的精确解图

图5.1绘制了该问题精确解图像,可见当参数ε很小时,解出现右边界层.

记Eh表示步长为h的最大误差,收敛率以下表格中xEm表示xm.

从下表5.1可见,当ε=1时不同数值方法其数值精度从低到高约可排序为: FD1,FD2,FD4,VDS1,VDS2,CDS,FD3,FD6,VDS3,FD5,HDS2,FD7,HDS3,HDS4.横向修正的差分格式的数值结果是最好的.因为计算机双精度数机器精度约为10−16,数值结果的误差越小时受到舍入误差影响越大,造成收敛率与理论分析不完全一致.因本文纵向系列修正差分格式是针对ε较小时设计的格式,数值结果也验证了横向修正差分格式更适宜求解ε较大时的问题.

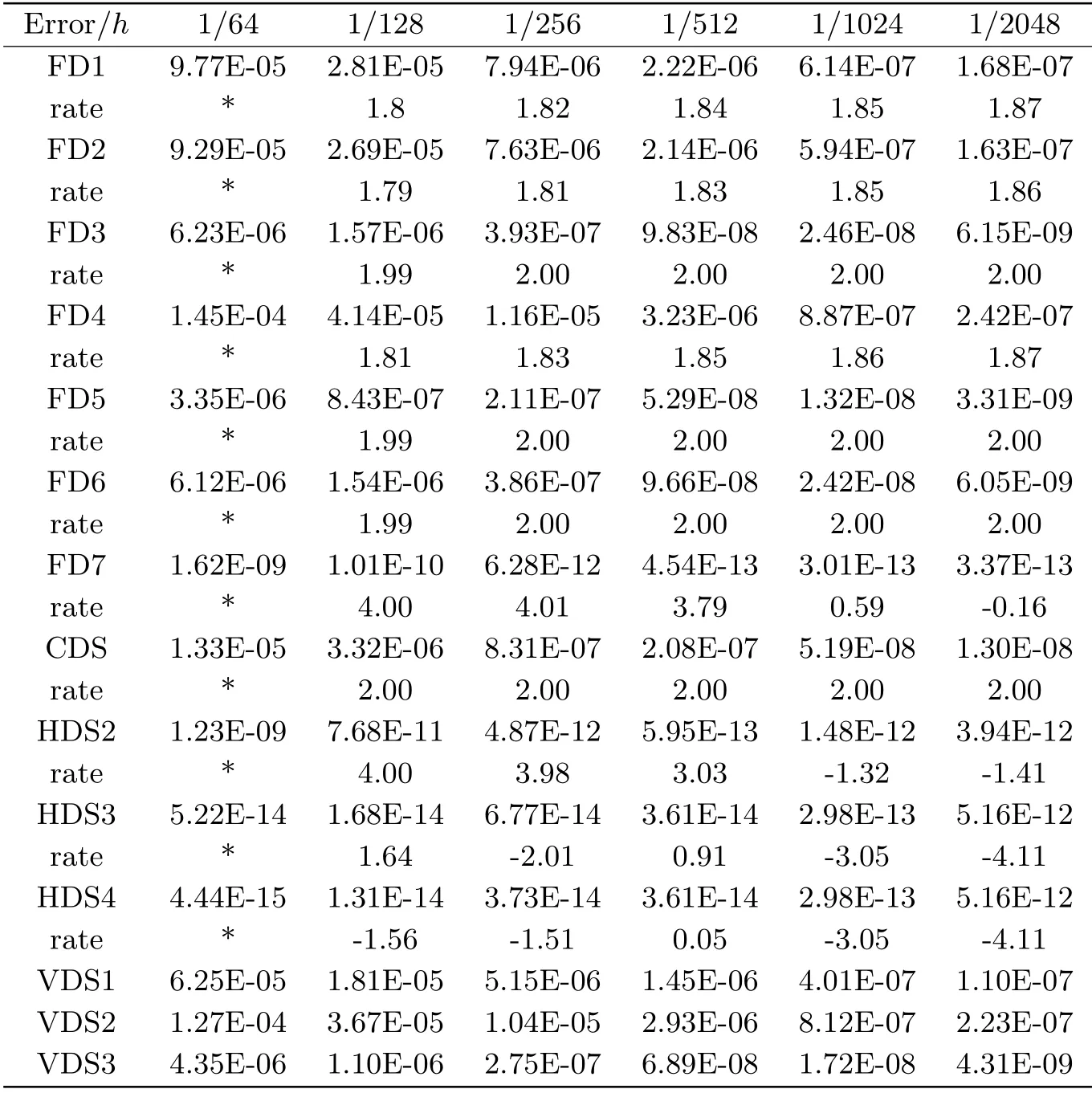
表5.1 算例5.1,当ε=1 时最大绝对误差及收敛阶比较

当参数ε=0.01时,表5.2中数值方法的精度从低到高约为: FD1,CDS,FD2,VDS1,FD3,FD7,HDS2,FD4,VDS2,FD6,FD5,HDS3,HDS4,VDS3.但与表5.1比较,随着参数ε的减小,横向差分格式的计算精度逐渐下降,而纵向差分格式计算精度逐渐提高,且此时本文的HDS3,HDS4,VDS3格式计算精度优于文献的七种参考格式.各种差分格式的计算收敛阶与理论分析基本吻合.

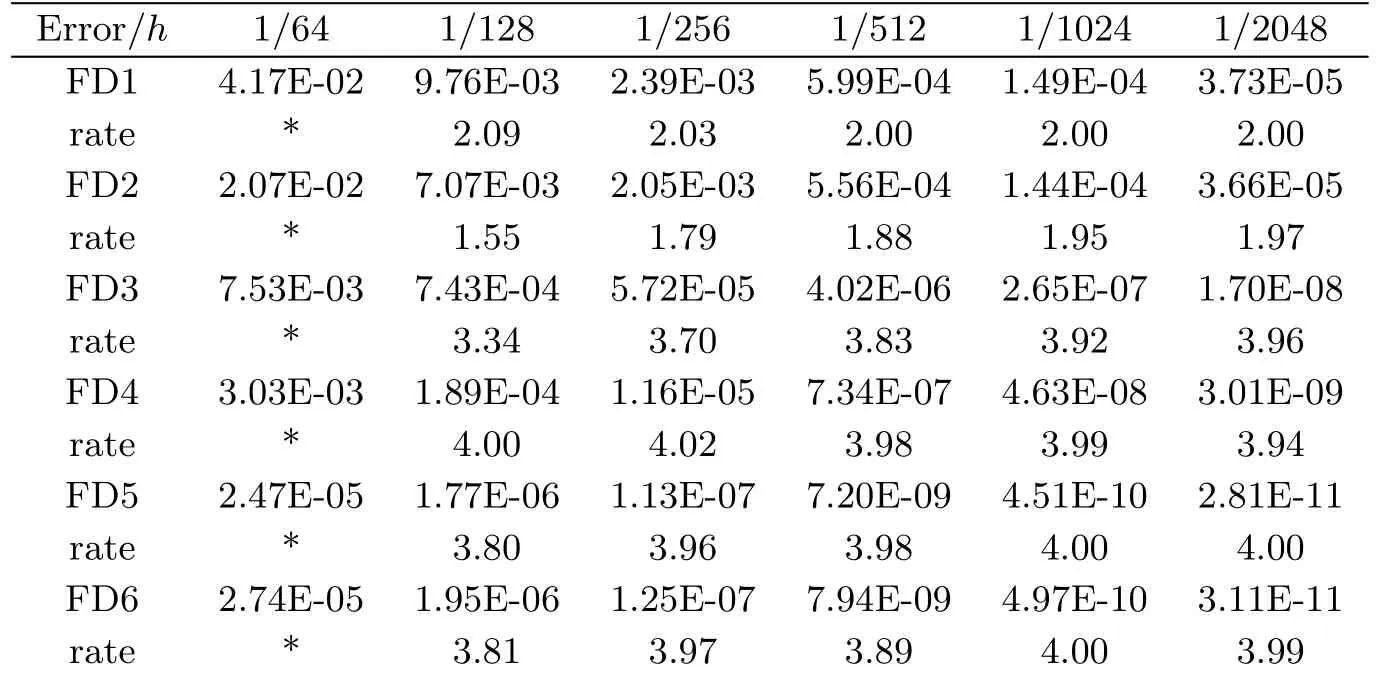
表5.2 算例5.1,当ε=0.01 最大绝对误差及收敛阶比较

FD7 8.66E-02 1.55E-03 5.89E-05 3.23E-06 1.94E-07 1.20E-08 rate * 5.80 4.72 4.19 4.06 4.01 CDS 8.55E-02 1.95E-02 4.64E-03 1.16E-03 2.90E-04 7.24E-05 rate * 2.14 2.07 2.00 2.00 2.00 HDS2 1.09E-02 7.58E-04 4.81E-05 3.06E-06 1.91E-07 1.20E-08 rate * 3.85 3.98 3.97 4.00 4.00 HDS3 7.45E-04 1.34E-05 2.12E-07 3.38E-09 5.25E-11 1.01E-12 rate * 5.80 5.98 5.97 6.00 5.70 HDS4 2.99E-05 1.35E-07 5.35E-10 2.23E-12 2.98E-13 1.30E-12 rate * 7.79 7.98 7.90 2.90 -2.13 VDS1 6.43E-04 1.80E-04 4.61E-05 1.17E-05 2.92E-06 7.31E-07 VDS2 3.25E-06 2.56E-07 2.38E-08 3.37E-09 6.77E-10 1.59E-10 VDS3 1.06E-08 2.09E-10 4.82E-12 1.17E-13 1.13E-13 1.57E-13

当参数ε=0.001时,表5.3可见各种方法的数值精度从低到高排列约为: CDS,FD1,FD4,FD7,HDS2,FD2,FD3,HDS3,FD6,FD5,VDS1,HDS4,VDS2,VDS3.与表5.1,表5.2中数据比较,随着参数ε减小,与差分格式设计初衷吻合,此时横向系列格式的计算精度变差,而纵向系列修正差分格式的数值精度明显优于横向系列格式,亦优于参考格式的计算精度,说明纵向格式更适宜求解参数ε较小的对流扩散问题.

表5.3 算例5.1,当ε=0.001 最大绝对误差及收敛阶比较

表5.4可见各种数值方法计算精度从低到高: FD1,FD4,FD7,CDS,HDS2,HDS3,HDS4,FD2,FD3,FD5,FD6,VDS1,VDS2,VDS3,参数变得更小时,文[3-9]中的FD1,FD2,FD3,FD4,FD7差分格式数值精度亦很低,而FD5,FD6数值精度较高.本文设计的横向差分格式数值精度也逐渐变差,但纵向修正差分格式VSD1,VSD2,VSD3数值精度越来越高,且优于参考格式计算精度,说明纵向修正差分格式更适宜于求解小参数奇异扰动问题.

表5.4 算例5.1,当ε=0.0001 最大绝对误差及收敛阶比较

小结: 实验结果与差分格式设计目的吻合,横向系列修正差分格式适合于求解ε较大时的对流扩散问题,而当ε较小时纵向系列修正差分格式数值精度更好.且本文设计的差分格式的数值精度优于文[3-9]中的差分格式的计算结果.我们亦针对另外两个算例进行了实验,得到了类似的结论,限于文章篇幅省略.