AN ABLOWITZ-LADIK INTEGRABLE LATTICE HIERARCHY WITH MULTIPLE POTENTIALS *

Wen-Xiu MA (马文秀)

School of Mathematics, South China University of Technology, Guangzhou 510640, China

Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia

Department of Mathematics and Statistics, University of South Florida, Tampa, FL 33620, USA

Department of Mathematics, Zhejiang Normal University, Jinhua 321004, China

College of Mathematics and Systems Science, Shandong University of Science and Technology,Qingdao 266590, China

Department of Mathematical Sciences, North-West University, Mafikeng Campus,Mmabatho 2735, South Africa E-mail: mawx@cas.usf.edu

Abstract Within the zero curvature formulation, a hierarchy of integrable lattice equations is constructed from an arbitrary-order matrix discrete spectral problem of Ablowitz-Ladik type. The existence of infinitely many symmetries and conserved functionals is a consequence of the Lax operator algebra and the trace identity. When the involved two potential vectors are scalar, all the resulting integrable lattice equations are reduced to the standard Ablowitz-Ladik hierarchy.

Key words Integrable lattice; discrete spectral problem; symmetry and conserved func-tional

1 Introduction

The inverse scattering transform is one of the powerful methods to solve Cauchy problems for nonlinear integrable equations, and it can also explain various geometrical and algebraic in-tegrable properties of nonlinear equations such as Hamiltonian structures and Virasoro algebras [1, 2]. The starting point of the direct and inverse scattering theory is a pair of matrix spectral problems (or a Lax pair [3]), which has a significant role in solving nonlinear integrable equa-tions. Other powerful theories on integrable equations, for example, Riemann-Hilbert problems [2], R-matrix theory [4], and Sato-function theory [5], also underline the importance of matrix spectral problems or Lax pairs.

It is important to search for nonlinear integrable equations from zero curvature equations,that is, compatibility conditions of pairs of matrix spectral problems, in both continuous and discrete cases. Among the well-known integrable equations are the KP-type continuous and discrete equations. The related KP theories are well developed, and the residue technique is systematically used to present sufficiently many conserved quantities required in showing integrability of the KP equations. For non-KP-type equations, the working techniques are varied[6]. The structures that integrable equations possess are very particular,and the involved nonlinearity causes difficulty in both the exploration of integrable properties and the construction of soliton solutions. It is particularly challenging to develop new ideas that are helpful in exploring multi-component integrable equations (see, for example, [7]).

We will focus on lattice equations within the zero curvature formulation. Let f be a lattice function. We specify the shift operator E and the inverse E−1of E as

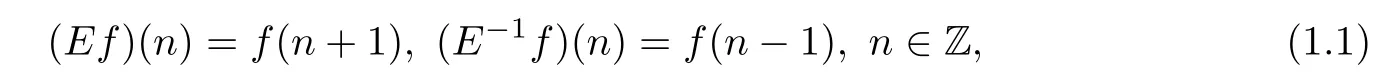
and always write

Moreover, it is known that the inverse operators of many discrete operators exist (see, for example, [8]). For example, we can have

In this article, we would like to generalize the standard Ablowitz-Ladik matrix spectral problem [11, 12]:

and consider a vector potential case of Q and R to construct a hierarchy of commuting multicomponent integrable Ablowitz-Ladik lattice equations. The basic technique to be adopted will be the discrete Lax technique or the technique of discrete zero curvature equations (see, for example, [8–10, 13]). Unlike the standard Ablowitz-Ladik case [14], the multi-component case has only one possibility to expand Lax operators in powers of λ, either positive or negative.Conclusions and remarks will be given in the last section.

2 A Multi-Component Ablowitz-Ladik Hierarchy

Let m ≥1 be a given integer. We consider a discrete arbitrary-order matrix spectral problem:

where Q and R are m-dimensional row and column vectors,respectively. The spectral problem(2.1) is a generalization of the standard Alblowit-Ladik one [11, 12], which corresponds to the case of m=1.

We solve a discrete stationary zero curvature equation

to generate an associated hierarchy of integrable lattice equations. A direct computation shows

when a solution is denoted by

where a is scalar, b is a row vector,c is a column vector,and d is an m×m matrix. Therefore,equation (2.2) equivalently requires

Then by the last three equations above, we can have

Thus, on the basis of the first equation in (2.4), we can take

to get a solution to the stationary zero curvature equation (2.2). Note that here it is crucial that the (1,1)-block in the spectral matrix U is assumed to be scalar.

Now, we assume that

We point out that the other way to expand in terms of negative powers of λ generally does not work, though it works well in the case of m=1 (see, for example, [14]). Once we take the initial data

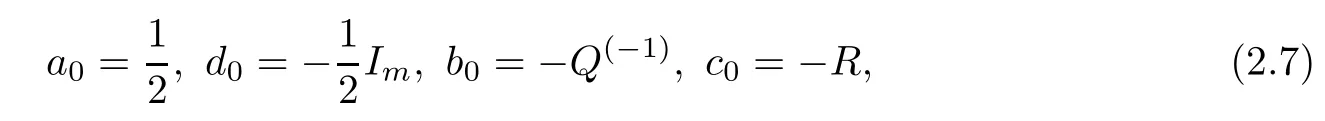
we can further have a recursion relation to determine all sets of ai,bi,ci, and di, i ≥1, as follows:

In particular, we can work out

We then take the Lax operators as follows:

where (P)≤0means taking non-positive power terms of λ in P, and we can directly see that the discrete zero curvature equations

give rise to a lattice hierarchy

where c−1=b−1=0. This can be written as

When m=1, (2.12) is reduced to the standard Ablowitz-Ladik hierarchy (see [14, 15]).

The first two lattice equations are

and

The inverse scattering transform and the Hamiltonian interpretation was presented for this nonlinear lattice equation (see, for example, [16, 17]).

3 Symmetries and Conserved Functionals

To show the existence of infinitely many symmetries of the lattice hierarchy (2.12), we can check the commutative property of the Lax operators (see, for example, [10]):

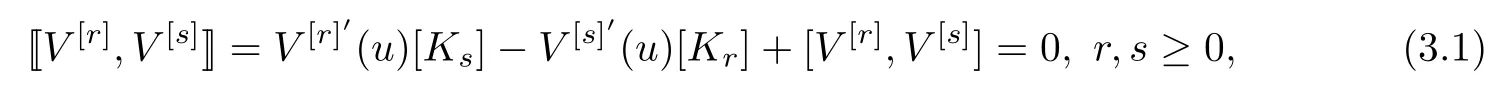
which ensures the existence of infinitely many common commuting Lie symmetries:

where Ks, s ≥0,are defined as in(2.13). In the above computations,P′stands for the Gateaux derivative of P with respect to u in a direction S:

Based on the theory of Lax operator algebras[10],it is only needed to check the commutativity ofat u=0, which can be easily observed:

Therefore, we do have an Abelian symmetry algebra (3.2).

When the underlying matrix algebra in the zero curvature formulation is simple,the associated zero curvature equations lead to classical integrable hierarchies[18, 19]; when semisimple,the associated zero curvature equations generate a collection of different integrable hierarchies;and when non-semisimple, we get hierarchies of integrable couplings [20], which require extra care in establishing their integrability. Particularly,we have the trace identity [9]

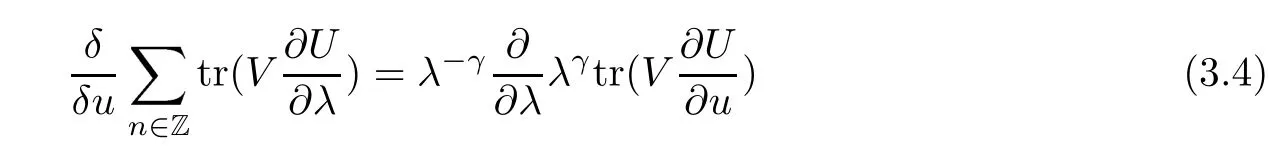
over simple or semi-simple matrix Lie algebras, and the variational identity [21]

over non-semi-simple matrix Lie algebras, where the bilinear form 〈·,·〉is symmetric, nondegenerate, and ad-invariant. In the above two identities, V =ΓU−1, and γ is a constant and can be computed by using Γ:

where Γ is a solution of the discrete stationary zero curvature equation (2.2).

For the spectral matrix U in (2.1), we have

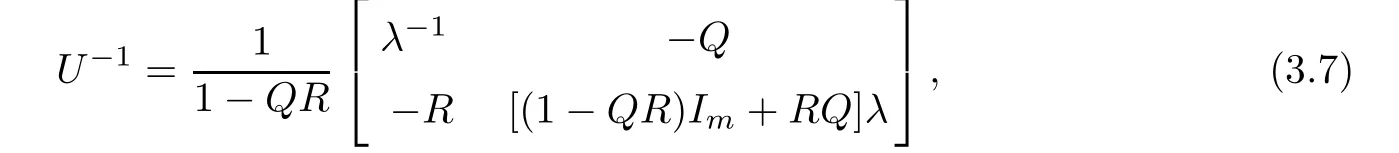
and therefore, we can work out

where V =ΓU−1.

Then, comparing the coefficients of λ in the trace identity tells that γ = 0, and thus, we have

where

As usual, it is a consequence of the Liouville integrability theory of zero curvature equations(see[9]for details)that all those functionalsare common conserved functionals of each equation in the lattice hierarchy (2.12). This can be precisely observed as follows. Note that we have an identity

which could be directly proved. Upon making two expansions

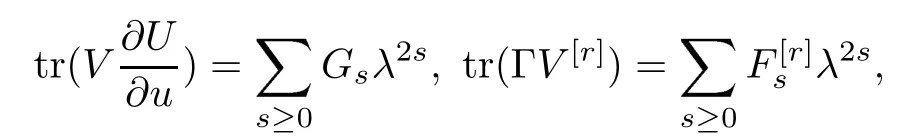
it follows that

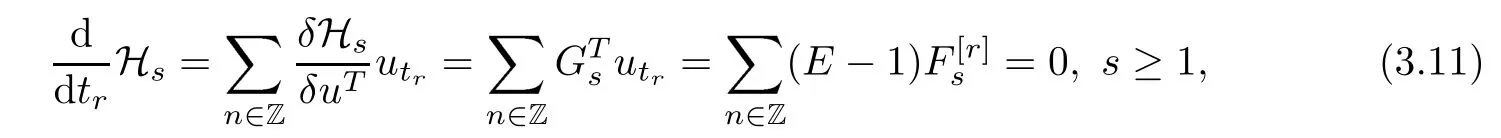
which means that each Hsis a conserved functional of the equation utr=Kr(r ≥0).

4 Concluding Remarks

We have generated a multicomponent Ablowitz-Ladik integrable lattice hierarchy from a discrete arbitrary-order matrix spectral problem, and presented infinitely many symmetries and conserved functionals, which are consequences of the Lax operator algebra and the trace identity, respectively. It should be interesting to study Darboux transforms, non-isospectral flows, and self-consistent sources for the resulting multi-component equations (see [22–25] for the Ablowitz-Ladik case).

Another generalization for the standard Ablowitz-Ladik spectral problem is as follows:

and this case uses the negative powers of λ for a solution Γ to the stationary zero curvature equation (EΓ)U −UΓ = 0. However, this is Gauge equivalent to the generalized matrix spectral problem (2.1) with two new potential vectors, Qnew= (Rrev)T= (Rm,··· ,R1) and Rnew=(Qrev)T=(Qm,··· ,Q1)T, and an exchange of λ ↔λ−1, because of

Therefore, in the case of m = 1, that is, the standard Ablowitz-Ladik case, we can have two expansions in terms of positive and negative powers of λ for the solution Γ (see [14, 15]).The question remains open whether one can derive an integrable lattice hierarchy from a more general spectral matrix

where m1,m2≥2 and P,Q are m2×m1and m1×m2potential matrices, respectively.

We remark that recent studies show plenty of lump and interaction solutions to integrable equations (see, for example, [26–32]), particularly between lumps and other kinds of exact solutions to nonlinear integrable equations in (2+1)-dimensions (see, for example, [33–36] for lump-kink interaction solutions and [37–39] for lump-soliton interaction solutions). All those supplements various theories of soliton solutions and dromion-type solutions, through basic techniques including the Hirota perturbation technique, symmetry reductions, symmetry constraints, and the Riemann-Hilbert approach (see, for example, [40–46]). It is believed that the existence of soliton solutions and interaction solutions to nonlinear equations should be a characteristic property of their complete integrability. It is definitely interesting to construct lump, soliton and interaction solutions to integrable lattice equations and identify nonlinear lattice equations that possess lump, soliton, and interaction solutions.