掘进巷道围岩变形分析与空顶时间确定

（山西霍宝干河煤矿有限公司，山西 临汾 041602）

1 工程概况

山西霍宝干河煤矿有限公司干河煤矿1#煤层中三采区辅助运输巷位于+80水平西翼，与+80水平西翼三条大巷垂直布置，巷道采用综合机械化掘进，巷道净宽4.8m、净高3.9m，设计长度1700 m。巷道老底、直接底、直接顶、基本顶由下至上分别为K7中粒砂岩、泥岩、砂质泥岩、K8中粒砂岩，其厚度分别为2.6m、4.6m、4.96m、3.12m，围岩力学参数见表1。巷道掘进过程中，掘进后空顶时长一般为30 min，有时出现围岩变形较大甚至局部片帮，通常认为是由于临时支护不及时导致，本文将对巷道掘进过程中的空顶时间开展研究。

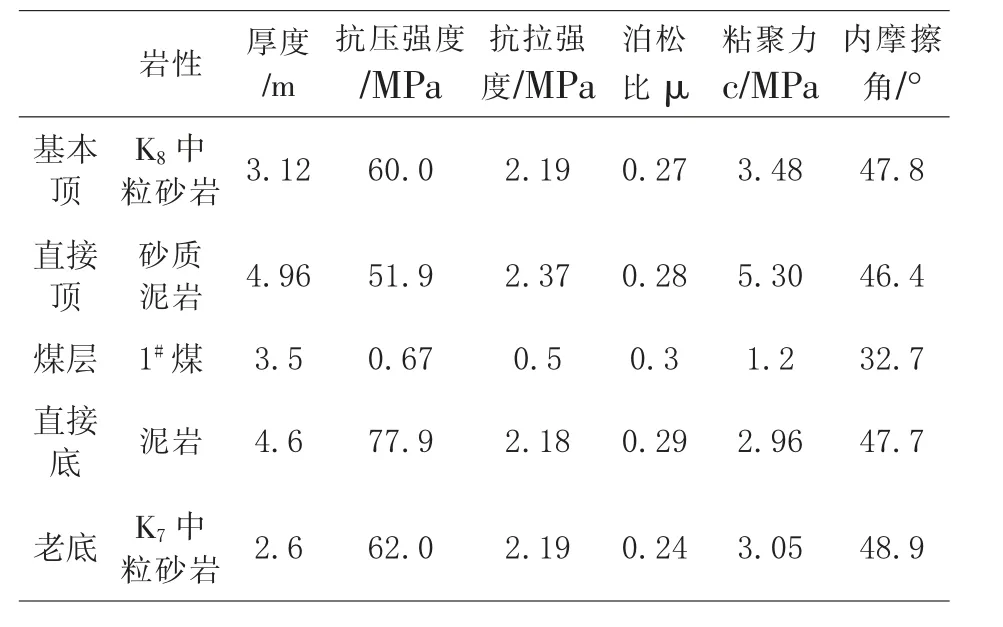
表1 三采区辅助运输巷围岩力学参数

2 巷道周边煤岩体变形分析

2.1 煤层界面应力分布

煤层巷道施工过程中，两侧煤体因围岩应力重新分布而产生塑性变形，巷帮煤层由浅入深分别为塑性区、弹塑性区及弹性区煤体[1-2]。煤层界面是指煤层与顶底板岩层的交界处，一般来说煤体粘聚力c和内摩擦角φ高于煤层界面的粘聚力c0和内摩擦角φ0，并且顶底板岩层泊松比μ0大于煤层泊松比μ。故巷道开挖后若不采取支护措施，会产生剪应力τxy作用于煤层界面，使煤体顶底板间挤出。煤层界面是煤体相对顶底板岩层运动时的滑移面，因此该界面上的切应力τxy与正应力σy满足应力极限平衡方程，即满足τxy=-|σytgφ0+c0|。并且在弹塑性区域与应力极限平衡交界位置处，即在x=x0时满足平衡方程

式中：A为侧压系数，H为巷道埋深，k为应力集中系数，γ为覆岩的平均容重，进一步求解得到=AkHγ。

通过联立求解上述两个平衡方程即可得到应力极限平衡区宽度x0见式（1）。

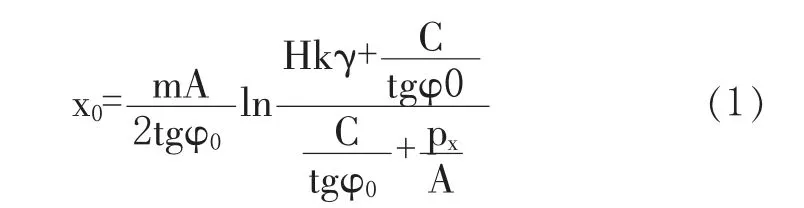
式中：px为支护阻力；m为所掘巷道的高度；C为煤柱与顶底板交界处的粘聚力。

2.2 煤帮应力分析

巷道掘进后围岩发生形变见图1。

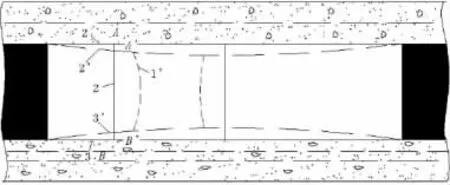
图1 掘进巷道围岩形变

煤体受压变形，是从弹性变形到塑性软化变形的过程，并且煤层在所受应力大于其极限抗压强度后，残留的强度仍可承载一定应力[3]。在煤帮深处x=x0处即为弹塑性交界处，这一区域煤体破坏程度低，但由于其处于屈服极限状态导致这一部分的应力最高，屈服函数为f（σ1，σ2，σ3）。在应力极限平衡区范围内变形是垂直应力σy=σ1产生的低围压作用下而变形的，这是由于该区内的垂直应力σy远大于水平应力σx，且σ1主应力与σy之间夹角较小导致。即当x=x0时：σy=σc，εy=εc，其中σc为单轴抗压应力极限，εc为与σc对应的应变。令x=0 即可得到σc的计算公式为：

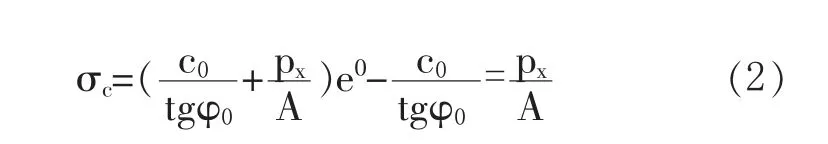
2.3 掘进巷道围岩变形分析

分析图1可以得到煤体在垂直方向上产生的应变为：εy=（σc-σy）ctgθ+εc，其中进一步得到垂直方向上产生应变量εy为：

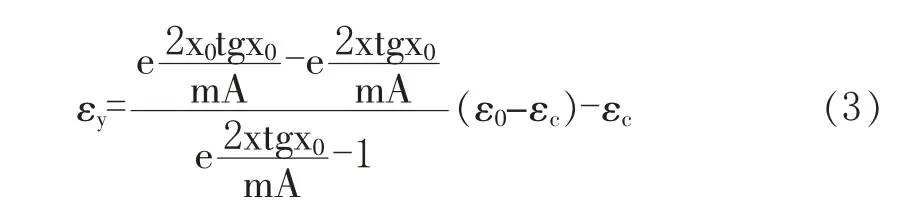
煤层在垂直方向上所受应力σy基本不发生变化，故应力作用下产生的应变εy与纵坐标y无关，因此煤体在垂直方向上的应变，即顶底板移近量为：

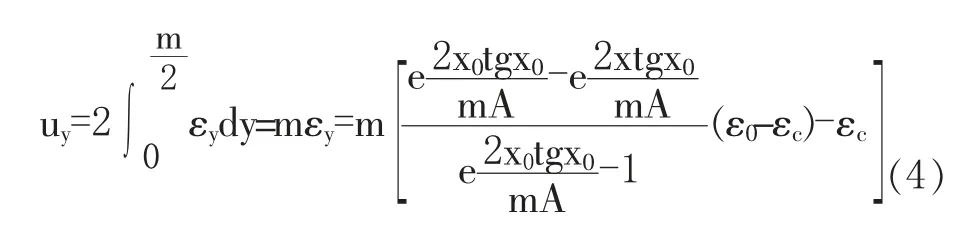
由于应力极限平衡区内的煤体为塑性状态，其所产生的体积应变可忽略不计。因此，应力作用下顶底板向巷道内移近时会将煤体从帮部挤入巷道，这一部分煤体的总面积与顶底板相对移近的总面积相同。而故巷道两帮的移近量为：

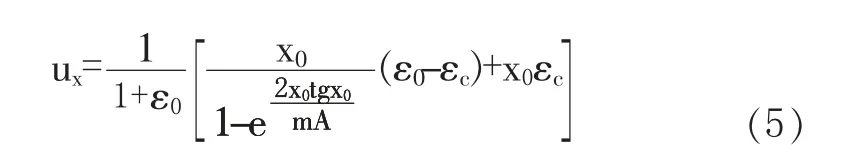
干河煤矿三采区辅助运输巷所处煤层均厚3m，平均埋深500m，煤层界面上的粘聚力C0为28.9 kPa，摩擦角φ0为27.7°，覆岩平均容重γ取26.8 kN/m3，侧压系数A取0.5，应力集中系数k取2，将上述参数代入式（5）可得到巷道空顶时间为30 min时，顶底板移近量达0.498m，两帮移近量达0.512 m。因此，需要在合理的空顶时间时进行支护，避免新掘巷道断面发生较大形变。

3 合理空顶时间确定

3.1 数值模拟分析

巷道开挖后，如未及时支护，新断面会在应力作用下发生明显变形，本节在借鉴其他掘进巷道建模经验[4-5]的基础上，借助有限差分软件FLAC3D建立数值分析模型，其模型长40m、高41.7m、宽29m，共划分约14万个网格，见图2，并假定目前掘进支护空顶距为3.5m，在空顶区间内设置位移监测点，分析不同空顶时长对围岩稳定性的影响。

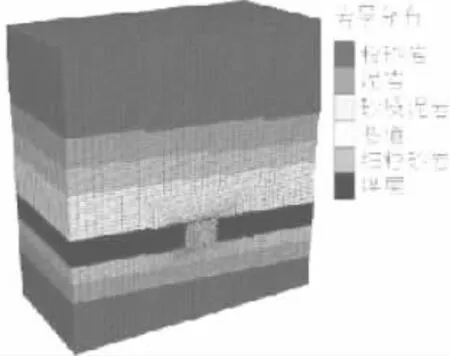
图2 模型建立

空顶40时步，即巷道开挖后4 min内围岩的变形及应力分布见图3。

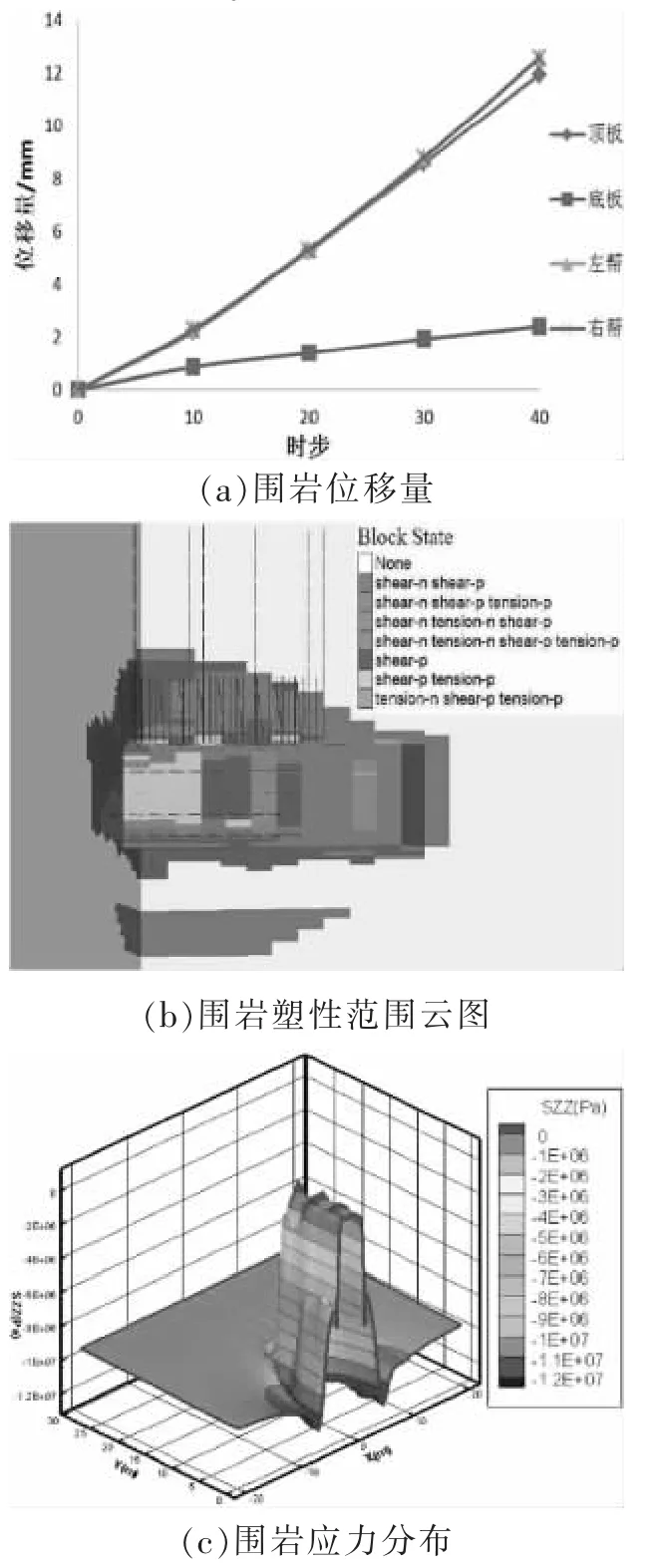
图3 空顶4 min 围岩的变形及应力分布

由图3可知：①巷道开挖后4 min内顶板下沉量及两帮移近量呈线性增加，两帮最大移近量与顶板最大下沉量分别为22.3 mm、12.1 mm；②掘进迎头并未承受明显的拉应力，空顶区内围岩均承受一定的拉应力；③距掘进迎头0.5～1m范围内的变形最为明显，该范围内顶板及两帮受拉应力影响产生了明显的塑性破坏，拉伸塑性破坏深度约0.2m，顶板与帮部由于剪切力造成的塑性破坏深度为0.5 m与2 m；④空顶区域内随着围岩深部及两帮距顶板中部距离的增加，所受应力逐渐减小；⑤巷道两帮产生12.83MPa应力集中的区域距巷帮表面0.5m，掘进迎头产生10.81MPa应力集中的区域距巷帮表面0.6 m。

空顶200时步，即巷道开挖后20 min内围岩的变形及应力分布见图4。

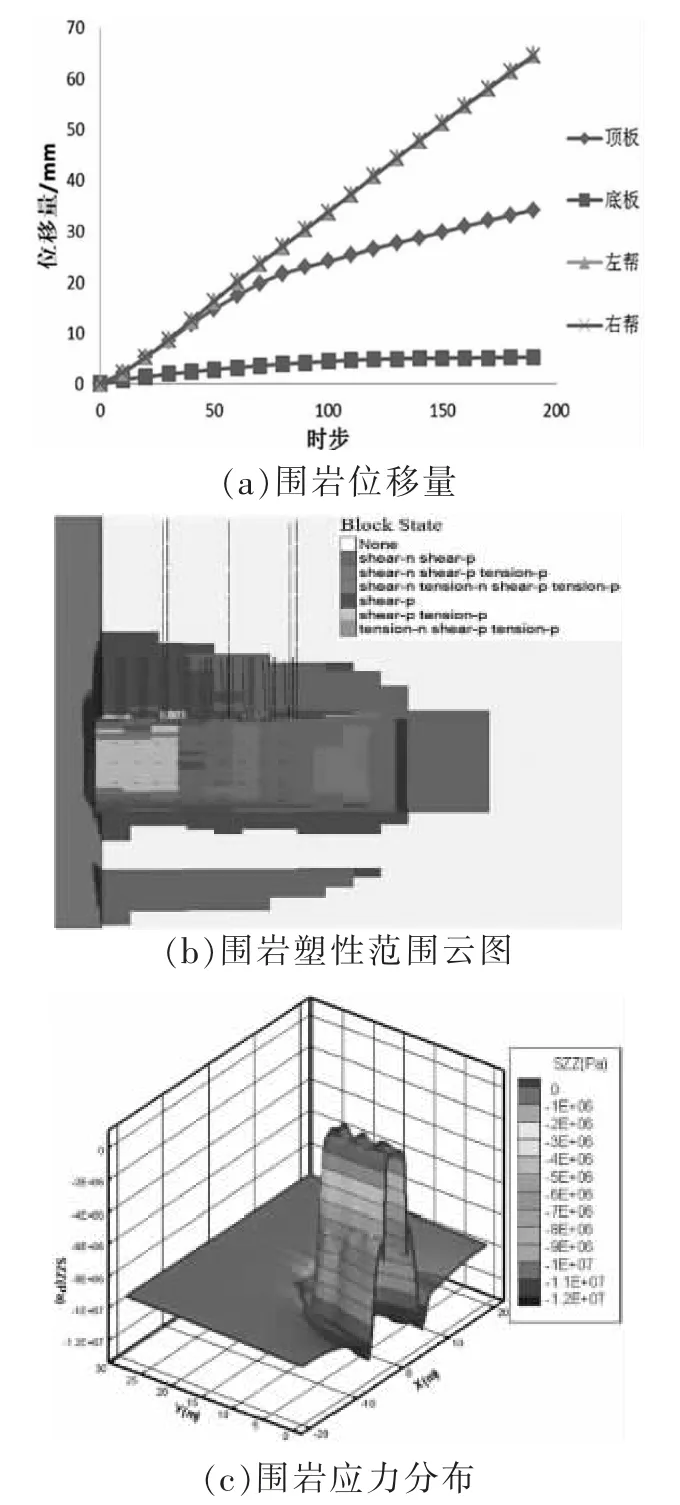
图4 空顶20 min时围岩的变形及应力分布

由图4数据可知：①巷道开挖后20 min内顶板下沉量及两帮移近量线性增加，70时步后顶板下沉量的增速降低，最终两帮最大移近量与顶板最大下沉量分别增加至71.1 mm、42.3 mm；②掘进迎头并未承受明显的拉应力，空顶区内围岩均承受一定的拉应力；③可以观察到距掘进迎头0.5～1m范围内的变形最为明显，该范围内顶板及两帮受拉应力影响产生了明显的塑性破坏，拉伸塑性破坏深度约0.4m，顶板与帮部由于剪切力造成的塑性破坏深度为2 m与3.5 m；④空顶区域内随着围岩深部及两帮距顶板中部距离的增加，所受应力逐渐减小；⑤巷道两帮产生12.59MPa应力集中的区域距巷帮表面2.1m，掘进迎头产生10.71MPa应力集中的区域距巷帮表面2.3 m。

空顶800时步，即巷道开挖后80 min内围岩的变形及应力分布见图5。

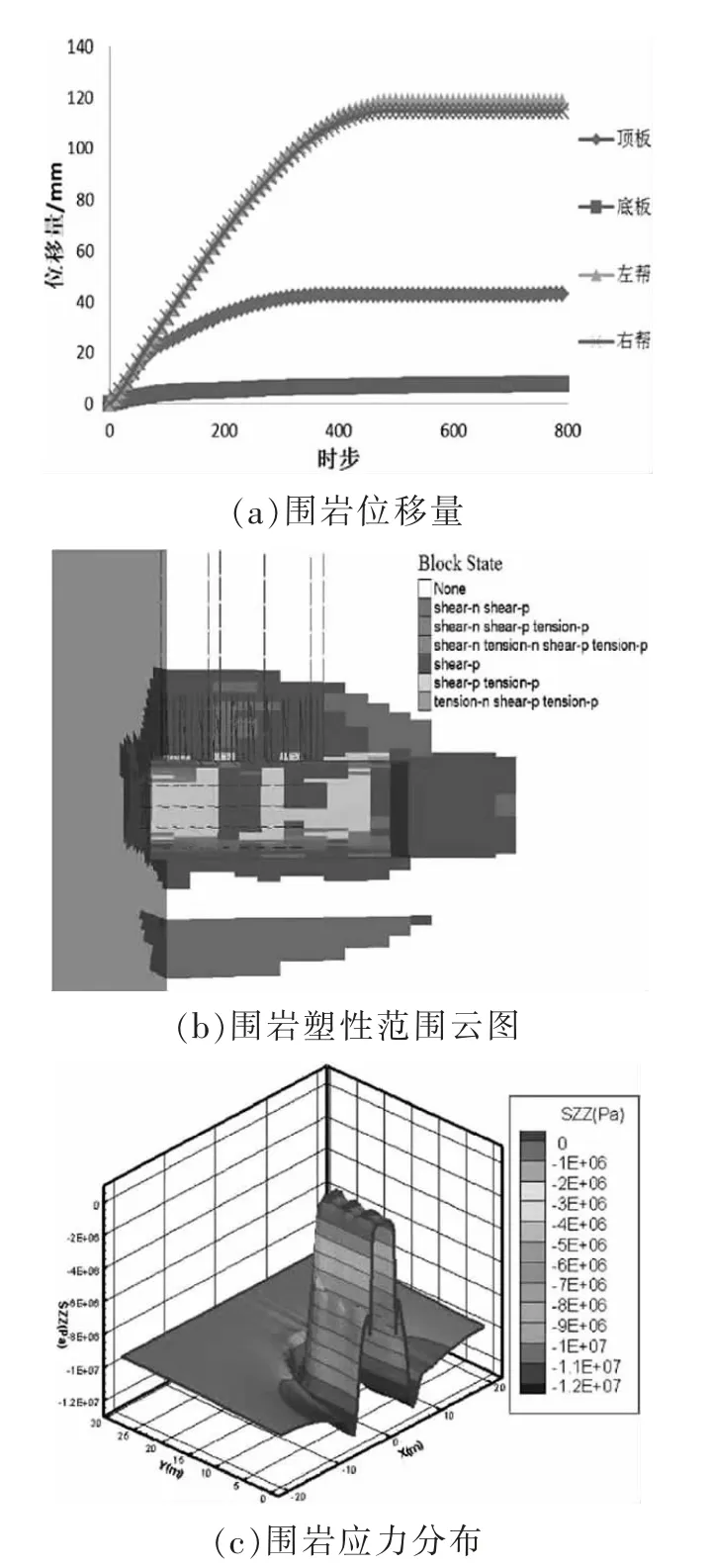
图5 空顶80 min时围岩的变形及应力分布

由图5数据可知：①巷道开挖后20 min后两帮移近量及顶板下沉量的增速进一步降低，40 min后基本稳定不再增加，两帮最大移近量与顶板最大下沉量分别稳定在240.1 mm、58 mm；②进迎头并未承受明显的拉应力，空顶区内围岩军承受一定的拉应力；③可以观察到距掘进迎头0.5～1m范围内的变形最为明显，该范围内顶板及两帮受拉应力影响产生了明显的塑性破坏，拉伸塑性破坏深度约0.4m，顶板与帮部由于剪切力造成的塑性破坏深度为2.5 m与5 m；④空顶区域内随着围岩深部及两帮距顶板中部距离的增加，所受应力逐渐减小；⑤巷道两帮产生12.42MPa应力集中的区域距巷帮表面3.5m，掘进迎头产生11.29MPa应力集中的区域距巷帮表面3.0 m。

通过分析4 min、20 min、80 min空顶时长下围岩变形及应力发现，掘进后空顶时间在4 min之内，围岩变形速率较快，围岩不稳定因素较多；空顶时间超过20 min后，围岩变形增速放缓，但两帮及顶板产生塑性破坏的深度达到2m，会造成支护时锚杆失效，因此需将掘进巷道的空顶时间控制在20 min以内。

3.2 现场实践效果分析

在三采区辅助运输巷掘进过程中，将空顶时间控制在20 min以内进行临时支护作业，即在现场掘进后需要在永久支护下进行临时支护准备作业，先将顶梁架设在机载前探支架上，并在顶梁上铺金属网临时固定，空顶时间接近20 min时再将机载前探支架升起并固定临时支护，确认安全后进行锚杆索永久支护作业、并同步布置围岩监测测站，对该断面的变形情况进行监测，监测结果见图6。

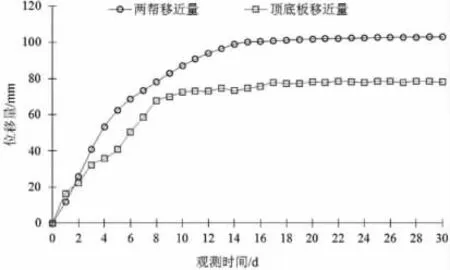
图6 围岩变形监测结果

由图6可以看出，三采区辅助运输巷掘进过程中将空顶时间控制在20 min以内进行支护作业，30天内顶底板最大移近量为80 mm、两帮最大移近量为100 mm，巷道围岩变形量均控制在有效范围内，临时支护效果较好。

4 结语

1）通过理论分析，三采区辅助运输巷掘进时空顶时间为30 min时，巷道顶底板最大移尽量为498 mm，两帮最大移近量为512 mm，围岩变形较大，影响新掘巷道断面；

2）借助有限差分软件FLAC3D分析空顶时间为4、20、80 min时围岩的应力分布及变形情况，发现将空顶时间控制在20 min时，未支护产生的塑性区宽度不会影响支护效果，得到三采区辅助运输巷掘进时合理的空顶时间为20 min。

3）当掘进工作面空顶时间控制在20 min时，巷道顶底板最大移尽量为80 mm，两帮最大移近量为100 mm，巷道断面变化较小，临时支护效果较好。