基于组合赋权VIKOR法的装备故障样本分配方法*
徐 达 周 诚 关 矗 李 闯
陆军装甲兵学院兵器与控制系,北京 100072
0 引言
故障样本分配是装备维修性验证试验的一项重要工作,分配到装备各组成部件的样本量是否合理,直接影响维修性验证试验结果的可信度。常规的故障样本分配是采用基于故障率的分层抽样方法或简单随机抽样方法,目前国内外相关标准和文献大都采用这一方法,但该方法仅考虑了故障率,容易造成故障样本分配结果不合理,如有些故障率低但危害性高的组成单元分配到的样本数量却很少,致使维修性验证试验结果可信度不高。
针对这一问题,近年来有许多学者做了大量的研究,主要集中在2方面:一是设法提高故障率的预测精度,不只局限于依据可靠性预计故障率的传统方法;如文献[1]提出了利用验前信息和Monte Carlo仿真相结合的方法计算故障率。文献[2]构建了广义加权组合预测模型,并与最小二乘法有机结合,有效提高了故障率预测精度。然而,这类方法从本质上仍是基于故障率进行样本分配,没有解决因素单一的问题。二是考虑多个影响因素。如文献[3]提出了一种基于多因子融合的故障样本分配方法,考虑了故障率、故障影响、单元重要度和维修费用4个影响因素。文献[4-7]也分别考虑了多个影响因素,旨在提高测试性验证试验中样本分配结果的可信度。但这类方法仍存在考虑影响因素不全面、确定各因素重要性权重时赋权方法单一,导致赋权结果片面等问题。
针对现有装备故障样本分配方法存在的不足,本文提出了一种基于组合赋权多准则妥协解排序法(简称VIKOR)的装备故障样本分配方法,依据故障
样本分配影响因素体系,采用AHP-变异系数法的主客观组合赋权法,确定各影响因素的权重,利用构建的基于组合赋权VIKOR法的故障样本分配模型实现试验样本的合理分配。
1 故障样本分配影响因素体系的建立
影响装备故障样本分配的因素有多种,进行故障样本分配时,构建完善的故障样本分配影响因素体系是确保分配结果合理的关键。通过分析装备实际使用情况,建立了包含故障率、严酷度、故障影响、单元重要度、维修时间和维修费用的影响因素体系,如图1所示。
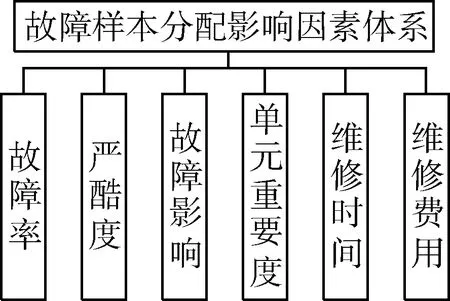
图1 故障样本分配影响因素体系
1)故障率。作为国内外相关标准及文献主要考虑的一个影响因素,可见故障率对样本分配结果影响很大。故障率可通过历史资料获得,也可通过Weibull分布、GA-BP神经网络等故障率预测模型获得。一般情况下,系统组成单元故障率越高,分配到的样本量越多。
2)严酷度。装备故障模式严酷度分析是进行危害性分析前的一项重要工作,根据故障影响的严重程度,常将严酷度等级分为以下4类:灾难的、致命的、中等的和轻度的[8]。引入梯形模糊数,如表1所示,有效消除了人为因素的影响。

表1 严酷度等级、分类准则及其梯形模糊数
3)故障影响。通常借助严酷度或扩散度等因素定量化描述故障影响程度。故障影响程度越大,该组成单元应分到越多的样本量。
4)单元重要度。系统组成单元重要度越高,表明该组成单元在系统中越重要,在故障样本分配时应分配到越多的样本数量。单元重要度定性描述及评分等级如表2所示。
5)维修时间。考虑到装备实际使用需求,维修时间应与分配的样本量成反比。
6)维修费用。维修费用是指在装备维修性验证试验过程中,所消耗的人力、物力和财力的总和。从开展试验的经济性角度考虑,维修费用越低,在故障样本分配时应分配到越多的样本数量。

表2 单元重要度及评分等级
2 影响因素权重的确定
采用层次分析法(AHP)-变异系数法的主客观组合赋权法确定影响因素权重,解决了单一主观或客观赋权方法赋权结果过于片面的问题,所得权重更加科学、合理,能够更加客观地反映出各影响因素在故障样本分配中的重要程度。
2.1 AHP法确定主观权重
层次分析法是一种充分利用专家信息处理决策问题的一种有效方法[9]。由专家对影响因素进行两两相对重要性比较,采用“1~9标度”法打分,得到判断矩阵T[10]:
T=[tij]n×n
(1)
式中:n为影响因素个数,tij表示第i个相对于第j个影响因素的重要度,

对T进行一致性检验。
CI=(λmax-s)/(s-1)
(2)
CR=CI/RI
(3)
式中:s为T的阶数,CI为一致性指标,RI为平均随机一致性,取值可参考文献[8]。
若CR<0.1,一致性检验通过,反之需要反复调整T直至通过。
2.2 变异系数法确定客观权重
变异系数法是一种直接利用各影响因素所包含的信息计算权重的客观赋权法[11]。
首先对原始数据无量纲化,计算变异系数:
(4)

各影响因素的权重为:
(5)

2.3 确定组合权重
按照一定的方法将主观权重和客观权重进行组合,可求得组合权重[12]。
采用“加法”集成法计算组合权重向量w=(w1,w2,…,wn)T。
其中:
(6)
式中:wi为第i个影响因素的组合权重,α为决策者对不同赋权方法的偏好程度0≤i≤1,0≤α≤1。
3 故障样本分配模型的构建
VIKOR是一种多准则条件下求解理想方案的决策方法[13]。构建基于组合赋权VIKOR法故障样本分配模型,首先根据装备客观指标数据,结合各影响因素的权重系数,确定正、负理想解,而后利用VIKOR法求出系统组成单元与理想解的相对贴近度大小,并以此为依据求解最优的样本分配方案。
设装备某系统有m个部件,n个影响因素。原始数值矩阵为:
X=[xij]m×n
(7)
式中:i∈[1,m],j∈[1,n]。
对X进行标准化处理,消除量纲并按效益型和成本型分类,得到规范化矩阵Y=[yij]m×n。
(8)
将Y与w相乘,得到加权标准化矩阵Z:
Z=[zij]m×n=[yijwj]m×n
(9)
计算正理想方案Z+和负理想方案Z-:
(10)
(11)

(12)
(13)

(14)
(15)
计算第i个部件的相对贴近度Ei:
(16)
Ei值越大,表示该部件应分配到越多的故障样本数量。
因此,系统第i个部件应分配到故障样本数量为Ni:
(17)
式中:ki为第i个组成单元的重要度,通常由装备订购方给出;li为第i个组成单元的数量,NZ为故障样本总量。
4 应用实例
装甲装备加温器是保证装备在寒区或冬季低温条件下平稳启动、正常发挥装备性能的关键,对提高装备全地域作战能力至关重要。以某型装甲车辆加温器维修性试验为例,采用基于组合赋权VIKOR法的故障样本分配方法对加温器各部件进行样本数量分配。该加温器原始数据如表3所示。
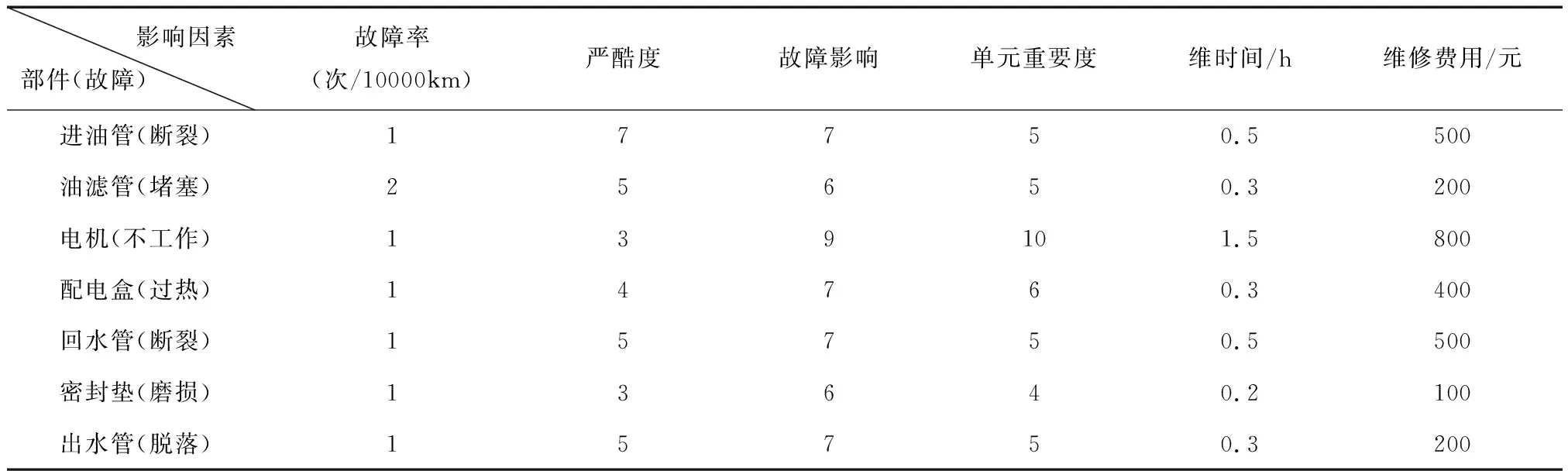
表3 故障样本分配原始数据
原始矩阵X:
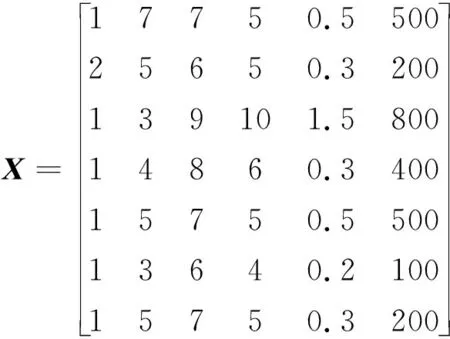
令α=0.5,计算组合权重:
w=(0.10,0.25,0.30,0.15,0.08,0.12)T
根据公式(8)和(9),计算加权标准化矩阵:
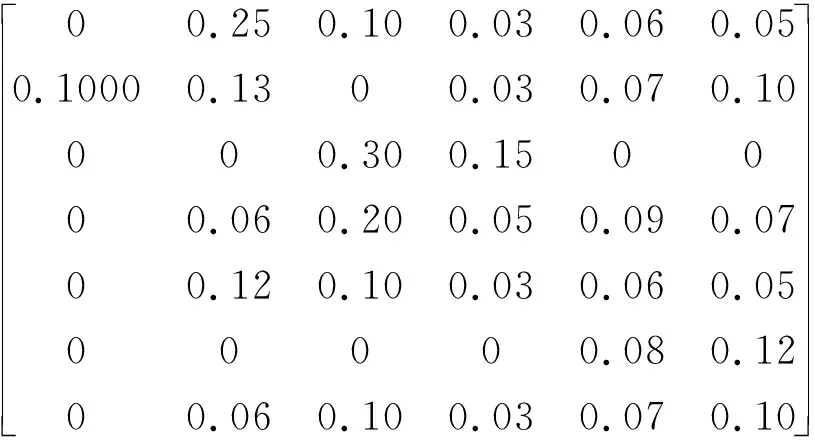
根据公式(10)和(11)计算Z+和Z-:
Z+=[0.25,0.13,0.30,0.20,0.13,0.12,0.10]
Z-=[0,0,0,0,0,0]
根据公式(14)和(15)对理想方案进行无量纲化:

根据公式(16)计算第i个部件的相对贴近度Ei:
Ei=[0.55,0.49,0.578,0.40,0.45,0.42,0.45]
令K=[0.15,0.15,0.2,0.1,0.15,0.1,0.15],L=[1,1,1,1,1,1],NZ=30,根据公式(17)计算第i个部件应分配到故障样本数量为Ni:
N≈[5,5,7,2,4,3,4]
基于故障率的按比例分层抽样方法和基于组合赋权VIKOR法的故障样本分配方法的分配结果如表4所示。

表4 两种方法的故障样本分配结果对比
由表4可知,对各部件分配的故障样本数量取整后,两种方法的故障样本总和分别是31和30。从故障样本分配结果来看,基于故障率的样本分配方法分配到各部件故障样本数量总体上比较均匀,而基于组合赋权VIKOR法的故障样本分配方法分配到各部件的样本数量与基于故障率的样本分配方法的分配结果明显不同,各部件分配到的故障样本数差别较大,如分配给电机、配电盒和密封垫的样本数量各减少了1个,分配给进油管和油滤管的样本数量各减少和增加了1个等,原因是本文所提方法考虑影响因素比较全面,综合权衡各因素在故障样本分配过程中的重要程度后,进行样本分配,而不是仅依据部件的故障率。
5 结论
综合考虑了故障率、严酷度、故障影响、单元重要度、维修时间和维修费用等因素对装备故障样本分配的影响,提出了一种基于组合赋权VIKOR法的故障样本分配方法,较好解决了装备维修性验证试验中考虑影响因素不全面的问题,采用AHP-变异系数法的主客观组合赋权法确定的影响因素权重更加客观,克服了单一赋权方法的不足,基于组合赋权VIKOR法故障样本分配模型实现了故障样本的合理分配,结合装备实例验证了所提方法的科学性和合理性,对新装备维修性验证试验具有较高的参考价值。

