正弦余弦算法的樽海鞘群算法

陈忠云 张达敏 辛梓芸

(贵州大学大数据与信息工程学院 贵州 贵阳 550025)

0 引 言

近年来，元启发式算法作为一种有效的演化计算技术，已受到众多学者的重视。元启发式算法是指受到生物行为和物理现象的启发提出的一类算法，其核心思想是实现搜索过程中随机性行为和局部搜索的平衡。常用的元启发式算法包括粒子群优化算法(Particle Swarm Optimization,PSO)[1]、正弦余弦算法(Sine Cosine Algorithm,SCA)[2]等。在解决众多多模态、离散和非差异的现实寻优问题中，元启发式算法呈现了优良的可操作性以及寻优能力，并成功应用于各种科学领域，如过程控制、生物医学信号处理、图像处理以及许多其他工程设计问题。

樽海鞘群算法 (Salp Swarm Algorithm,SSA)是2017年由Mirjalili等[3]提出的一种新型群智能算法，具有结构简单、参数少、容易实现等优势，但仍存在求解精度低和收敛速度慢等缺陷。文献[4]将樽海鞘群算法中跟随者单步位置更新方式改为两步，分别根据自适应平局移动策略和领域最优引领策略进行更新，再引入方向学习策略以一定概率对个体位置进行扰动，提高种群多样性，使算法跳出局部最优。文献[5]提出固定惯性权重，可以加快搜索过程中的收敛速度，并应用于特征选择问题。文献[6]结合樽海鞘群算法和混沌理论提出混沌樽海鞘群算法，在解决特征提取问题时，能发现最优特征子集，最大限度地提高分类精度，最小化所选特征的数目。文献[7]提出基于樽海鞘群算法的无缘时差定位，利用SSA解决TDOA定位结算问题，验证算法在多站时差定位问题上的有效性与优越性。文献[8]提出基于Logistics混沌方法对粒子进行初始化，增加初始个体多样性。文献[9]将正弦余弦算法作为一种局部算法嵌入到花授粉中，对花粉个体分别进行正弦和余弦优化。文献[10]提出差分演化策略，可增强算法的局部开采能力。

为解决标准樽海鞘群算法存在的求解精度不高和收敛速度慢等问题，本文提出一种正弦余弦算法的樽海鞘群算法(Salp Swarm Algorithm Using Sine Cosine Algorithm,SCSSA)。选用Logistics映射来生成樽海鞘群算法的初始种群，增强初始个体的均匀性。种群个体更新后，将正弦余弦算法作为局部因子嵌入到樽海鞘群算法中，并对最优樽海鞘个体采用差分演化变异策略，有助于增强算法的全局探索和局部开发能力。通过求解8个典型复杂函数的最优解来验证正弦余弦算法的樽海鞘群算法的有效性。

1 樽海鞘群算法

樽海鞘群算法[3]是Mirjalili等提出的一种全新的智能优化算法，其思想源于樽海鞘的聚集行为，即樽海鞘链。它以水中的浮游植物(海藻等)为食，通过吸入喷出海水完成在水中的移动。在樽海鞘群算法中，樽海鞘链由两种类型的樽海鞘组成：领导者和追随者。领导者位于樽海鞘链的最前面，而其他个体则为追随者。

该算法定义每个樽海鞘个体的位置向量X用于在N维空间中搜索，N是决策变量的数目。X将由维度为d的N个樽海鞘个体组成。因此，种群向量由N×d维矩阵构成：

(1)

在樽海鞘群算法中，食物源的位置是所有樽海鞘个体的目标位置。因此，领导者的位置更新公式为：

(2)

由式(2)可知，领导者位置更新主要受到食物源位置影响。系数c1是樽海鞘群算法中最重要的参数，其可以使SSA的探索能力和开发能力处于平衡状态。c1定义如下：

c1=2e-(4t/Tmax)2

(3)

式中：t为当前迭代次数；Tmax为最大迭代次数。

利用牛顿运动定理更新追随者的位置：

(4)

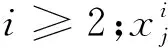
(5)

因此，由式(2)和式(5)可以模拟樽海鞘链的行为机制。

2 算法设计

2.1 Logistics映射的种群初始化

樽海鞘群体的初始化对SSA的收敛速度和寻优精度至关重要。在樽海鞘群初始时，由于没有任何先验知识可使用，基本上大部分群智能算法的初始位置都是随机生成的。初始种群均匀分布在搜索空间，对提高算法寻优有很大帮助。

混沌序列具有随机性、遍历性和规律性，通过其产生的樽海鞘群体有较好的多样性。其基本思路是：通过映射关系在[0, 1]区间产生混沌序列，然后将其转化到个体的搜索空间。产生混沌序列的模型有许多，本文采用Logistics映射生成的混沌序列来初始化樽海鞘群算法群体。Logistics映射的数学表达式为：

(6)

式中：μ∈[0, 4]是混沌参数，μ越大，混沌性越好，本文取μ=4；i= 1,2,…,N表示种群规模；j= 1,2,…,d表示混沌变量序号。

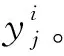
(7)

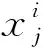
2.2 正弦余弦算法(SCA)

由式(5)追随者位置更新公式可知，第i只樽海鞘位置会根据第i和i-1只樽海鞘位置坐标中点进行更新。在此过程中并没有判别xi是否优于原来位置，这种单方向根据第i只樽海鞘的位置信息机制，樽海鞘个体之间缺少交流，信息利用率较低。为使群体之间拥有更多的交流机会，进一步优化樽海鞘群算法的探索和开发能力，本文引入正弦余弦算法[2]作为局部优化算子嵌入到樽海鞘群算法中，即在更迭后期对全部樽海鞘个体采用正弦余弦操作，指导樽海鞘个体更新樽海鞘位置，更新公式如下：

(8)

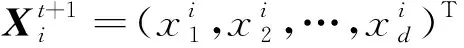
正弦余弦优化策略的嵌入，一方面能够很好地填补樽海鞘群算法位置更新公式存在依赖性的缺陷，无论是正弦机制还是余弦机制，樽海鞘个体都能够与食物源进行位置交流，促进最优信息在种群中得到传递，每一个樽海鞘个体都能较好运用自身和食物源的位置差信息，促使樽海鞘个体朝向最优解移动；另一方面，使得樽海鞘个体进一步在同一个搜索空间的不同范围中进行全局搜索和局部开发。正弦机制可使全局搜索找到最优解降低余弦机制的寻优盲点，减少樽海鞘个体陷入局部最优，而余弦机制可使局部开发填补正弦全局搜索收敛速度满的缺点，提高探索能力，加快算法收敛。正弦余弦的相互使用，可较好平衡算法的探索和开发能力，共同促进算法性能的优化。

2.3 差分演化变异策略

(9)

式中：F是缩放因子；R1、R2、R3、R4是区间[1,N]上互不相同的随机整数，代表不同樽海鞘个体；j是维度；mj为扰动后的食物源位置。使用式(10)交叉操作选择新的食物源位置。

(10)

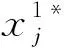
2.4 SCSSA步骤

正弦余弦算法的樽海鞘群算法步骤如下：

Step1初始化个体位置。使用Logistics映射生成混沌序列，根据搜索空间的上下限，把混沌序列逆映射为一个N×d维的矩阵。

Step2计算初始适应度值。根据测试函数计算N个樽海鞘的适应度值。

Step3选定食物源。将Step2中计算后的适应度值升序(或降序)排列，适应度值最好的樽海鞘位置选定为食物源位置。

Step4更新领导者和追随者位置。确定食物源位置之后，选取种群中一个的樽海鞘个体根据式(2)更新领导者位置，其余的樽海鞘根据式(5)更新追随者位置。

Step5正弦余弦指引策略。利用式(8)对Step4所生成的樽海鞘个体进行正弦或余弦操作，以更新到新的樽海鞘位置。

Step6计算适应值。计算更新后种群的适应度值，引入差分演化变异策略，根据式(9)和式(10)更新食物源位置。

Step7重复Step4-Step6，如果达到设置的精度要求或规定的最大迭代次数，则终止算法，输出全局最优解。

3 仿真实验

为了验证本文提出的SCSSA在求解优化问题上的有效性和鲁棒性，将SCSSA与标准的SSA[3]、PSO以及SCA在8个典型的标准测试函数上进行仿真实验，在最优值求解上独立进行50次对比实验。8个复杂函数如表1所示，其中包含单峰、多峰等不同特征的测试函数。单峰函数为在定义上下限内只有一个严格上的极大值(或极小值)，通常用来检测算法收敛速度。多峰函数为含有多个局部最优解或全局最优解的函数，经常用于检测算法探索能力和开发能力。测试函数维度设置为50维。

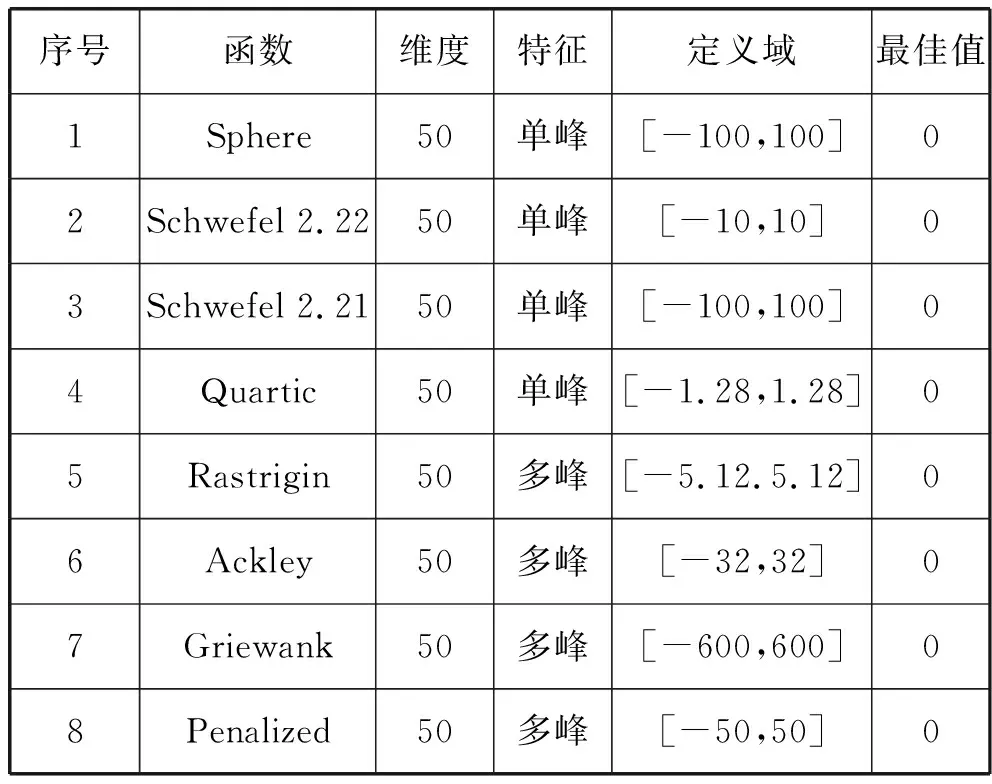
表1 基准函数

实验环境为：Windows 7系统，8 GB内存，CPU 2.5 GHz，算法基于MATLAB 2014b用M语言编写。实验最大迭代次数为1 000，种群个数为30，各算法参数设置如表2所示。

表2 算法参数设置

表3记录了50次独立实验后各算法寻优结果的最佳值(Best)、平均值(Mean)、标准偏差(Std)、求解成功率(SR/%)和平均耗时(Time/s)等数据。其中求解成功率为计算成功次数除以本次实验的求解次数。判断一次求解是否成功的公式如下：

(11)

式中：FA为每次实际求解最佳值；FT为测试函数理论最佳值。

表3 各算法的寻优结果

最优值、平均值都可以反映算法的收敛精度和寻优能力。对于4个单峰函数(f1-f4)，SCSSA在求解精度上最高达到1.00E-40。求解f3(Schwefel 2.21)时，SSA和SCA的求解能力很差，与理论最优值存在1.00E+01级的误差。而SCSSA的寻优精度相比SSA、PSO和SCA都更好，且求解精度变化不大。对于4个多峰函数(f5-f8)，SCSSA在求解f5和f7(Rastrigin和Griewank)的精度时获得了理论最优值0，且SCSSA较其他3种算法仍然具有很好的寻优精度。因此，SCSSA在求解单峰、多峰的基准函数时都有更好的寻优效果。

标准差和成功率可以反映算法的稳定性和跳出局部最优的能力。由表3可知，SCSSA独立50次计算的标准差始终比其他三种算法都要小。这说明SCSSA对于低维和高维基准函数的寻优求解有着很好的稳定性，且在多峰函数上寻优能力比较强，跳出局部最优的能力相比其他算法更好。8个基准函数中有单峰和多峰，除了Penalized这个多峰基准函数外，SCSSA在成功率基本上为100%，而标准SSA在f1的成功率为100%，但在其余基准函数的成功率几乎为0。SSA在寻优求解能力上的表现有很大不足，特别是在求解f3和f5时，标准差和成功率都较差，说明标准SSA在跳出局部最优的能力是较弱。而在SCSSA中引入正弦余弦优化策略，对算法后期跳出局部搜索具有很大作用。

从平均耗时来看。SCSSA相对于标准SSA的平均耗时都要大，PSO总体运行时间均优于SCSSA、SSA和SCA。SCSSA在SSA的基础上引入多个算子，使得算法能够搜索到更多的解，同时增加了算法运行时间。总体来看，SCSSA平均耗时的增加不大，在允许范围内。

基于50次独立运行算法的平均值和标准差不会比较每次运行结果。Derrac等[11]提出，对于改进进化算法性能的评估，应该进行统计检验。为了判断SCSSA的每次结果在统计学上是否明显与其他算法的最佳结果不同，在5%的显著性水平下进行Wilcoxon统计检验。表4为所有基准函数的SCSSA和其他算法的Wilcoxon秩和检验中计算的p-value。例如，如果最佳算法是SCSSA，则在SCSSA/SSA, SCSSA/PSO、SCSSA/SCA等之间进行成对比较。由于最佳算法无法与自身进行比较，因此，针对每个函数中的最佳算法标记为N/A，表示“不适用”。这意味着相应的算法在秩和检验中没有统计数据与自身进行比较。符号“+”“?”和“≈” 分别表示SCSSA的性能要优于、劣于和相当于对比算法。p-value小于0.05的可以被认为是拒绝零假设的有力验证。

表4 Wilcoxon 秩和检验的p-value

可以看出，SCSSA的p-value全部小于0.05，这表明其优越性在统计学上是显著的，即SCSSA比其余算法具有更高的收敛精度。

选择平均绝对误差MAE作为评价指标对算法进行定量分析，结果如表5所示。

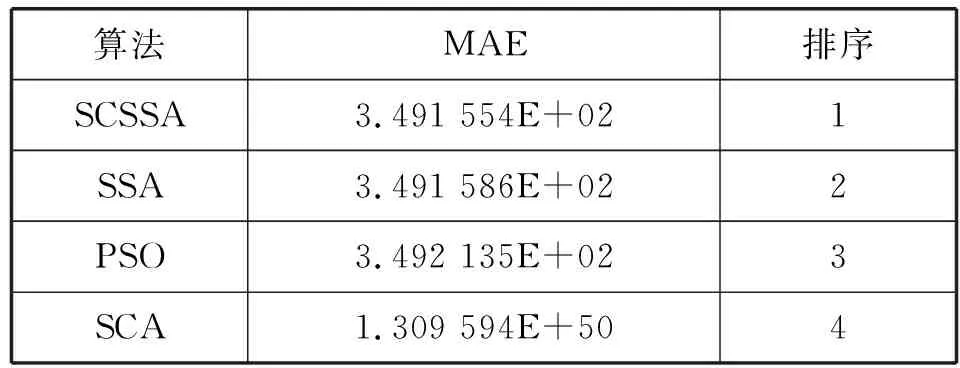
表5 MAE算法排名

MAE的计算公式为：

(12)

式中：mi为算法产生的最有结果的平均值；oi为相应基准函数的理论最优值；Nf为基准函数个数。

可以看出，SCSSA排名均为1，与另外3种算法相比，SCSSA提供了最小的MAE，进一步证明了SCSSA的有效性。

图1为8个基准函数在50维的平均收敛曲线。由于不同算法收敛精度存在较大差异，为了便于观察收敛情况，本文对寻优适应度值(纵坐标)取10为底的对数。由图1(a)-(d)可看出，SCSSA的收敛曲线下降最快。在迭代前期，SCSSA有一小段时间收敛曲线下降很快，这说明引入Logistics映射初始化种群增加了种群多样性，使得算法前期收敛速度就较快，且随着更迭次数的增加持续寻优，未出现停止状况。由图1(b)和(c)可知，SCA、PSO和SSA在迭代后期出现不同程度的停滞，且寻优精度较低。

图1(e)-(h)是多峰函数的平均收敛曲线。SCSSA引入Logistics映射初始化种群算法的收敛性在f5-f8上迭代前期收敛速度很快，这也进一步说明使用Logistics映射初始化种群的作用。在迭代后期，虽然SCSSA收敛速度较前期平缓，但也一直在寻优，而其他3种算法后期基本都陷入局部最优，出现不同程度的停滞现象。SCSSA最终的寻优精度较其他算法仍然表现较好。无论单峰、多峰，还是低维和高维，对于每个基准函数，SCSSA比其他算法的收敛速度和寻优精度都更佳。由表3可知，对于函数f5、f7，SCSSA的最佳值为0，故图1(e)、(g)中，SCSSA曲线的后面部分未显示。

图1 基准函数平均收敛曲线

综上可知，正弦余弦算法的樽海鞘群算法对于所有基准函数都有很好的寻优结果，特别是对于多峰的函数，具有较好的稳定性和寻优能力。

4 结 语

本文在标准樽海鞘群算法的基础上，引入混沌映射和使初始化种群均匀分布，将正弦余弦算法嵌入樽海鞘算法中，更好地平衡探索和开发能力，最后加入差分演化变异策略使算法易于跳出局部最优。本文提出一种改进的正弦余弦算法的樽海鞘群算法，并将其应用于复杂函数的寻优问题中。不仅使用最优值、标准差等指标对算法进行检验，还提出使用Wilcoxon秩和检验对算法显著性水平进行验证。研究表明：基于正弦余弦算法的樽海鞘群算法可以获得更好的全局搜索和局部搜索能力，且收敛到质量更好的最优解，算法的有效性和鲁棒性也得到验证。