基于Lyapunov 稳定性的风机速度渐近跟踪控制

于江波刘怡彤石啊莲

(1.山东建筑大学 理学院，山东 济南250101；2.齐鲁师范学院 数学学院，山东 济南250200)

0 引言

稳定性是现代系统与控制科学的重要概念。 早在2000 年前，古代中国的汉朝淮南王刘安所著的《淮南子·说山训》中就曾指出“下轻上重，则覆必易”，这是中国古代出现的对稳定性概念的最初理解[1]。 1892 年，李雅普诺夫(Lyapunov)发表了著名的博士论文《运动稳定性一般问题》，利用柯西关于微积分极限描述的ε - δ语言，将常微分方程解对初值的连续依赖由有限时间拓展到无穷时间区间，给出了有关稳定、渐近稳定的科学概念，开创了运动稳定性的一般理论。 自此，李雅普诺夫稳定性理论在系统理论与工程应用中起着愈来愈重要的作用[2]。

众所周知，非线性微分方程难以求得解析解[3-5]。 李雅普诺夫稳定性理论的一个强大功能是在不必已知方程解的情况下，通过选取李雅普诺夫函数的方法，就可以判定解的某些性能，这为人们认识更广泛的非线性微分方程提供了重要工具。20 世纪90 年代发展起来的反步法(Backstepping)是非线性系统控制理论的一个突破[2]，其将复杂的非线性系统分解为不超过系统阶数的子系统，为每个子系统选取李雅普诺夫函数和虚拟控制量，按照负反馈调节方式，一直后退到整个系统，最后完成整个控制律的设计。 应用反步法可以解决一大类形如下三角形式的非线性系统控制设计与李雅普诺夫稳定性问题[6-10]。

文章将应用李雅普诺夫稳定性理论结合反步法研究风机速度控制系统的速度控制问题。 风机是一类依靠输入的机械能提高气体压力并排送气体的机械装置，目前已广泛应用于矿井、矿山、矿井、隧道、船舶和建筑物的通风、排尘、冷却中。 风机关系到系统的输配能耗，是建筑节能非常关键的部分。 针对一类由直流电动机驱动的风机速度控制系统，近年来已有大量的研究。 Freeman 等[11]研究了电流可测情况下的风机速度控制；Jiang 等[12]随后提出了电流不可测情况下的速度控制器；Wu 等[13]进一步在电流不可测、电感系数未知的情况下，基于黎卡提微分方程的观测器设计了速度控制器；Wu 等[14]利用时变卡尔曼滤波器实现了外部扰动情况下的风机速度控制；Yu 等[15]通过拟符号函数技术实现了风机速度对于任意设定速度的实用跟踪控制。 但是上述文献中针对风机系统的研究，都是基于理想情况下转动负载是风机速度的线性函数的假设，然而直流电机本身是一个非线性系统，且多变量、非线性、强耦合的控制对象，从电机电流和励磁的非线性变化来看，运用非线性的控制方法更加合理、准确[16]。Freeman 等[11]也指出，转动负载实际上是与风机速度成正向增长关系的非线性函数。

因此，文章针对转动负载是不确定的非线性函数情况，探讨了风机系统的速度跟踪控制问题。 应用李雅普诺夫稳定性理论进行了系统稳定性分析，基于矩阵相似变换的方法对风机系统再建模，避免了现有文献中需要在反馈设计前进行一个预前反馈的假设。 引入动态辅助变量对未知参数进行估计，并应用反步法设计了速度控制器，通过Matlab 仿真软件验证能否实现风机速度对于任意给定的设定速度的渐近跟踪控制并保持稳定。

1 李雅普诺夫稳定性定义及相关结论介绍

一阶时变微分方程由式(1)表示为

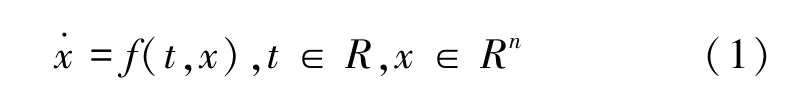
式中:f为关于t分段连续和x满足局部Lipschitz 条件的非线性函数，f: [0，∞)× D→Rn，其中D为包含原点x =0 的定义域，D⊂Rn。 如果满足式(2):

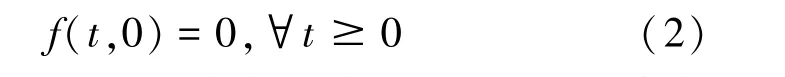
则称原点是一阶时变微分方程式(1)的一个平衡点(或零解)。

假设可微函数x = φ(t) 是微分方程式(1)的一个非零解，可利用变换y =x - φ(t) 将式(1)转化为(t，y) 其中g(t，y)=f(t，y +φ(t))-f(t，φ(t))且g(t，0)=0，因此式(1)的非零解可转化为微分方程(t，y) 的零解，从而要研究式(1)的解x =φ(t) 的性态，只需研究其零解的性态即可。

微分方程(组)平衡点的李雅普诺夫稳定性定义和李雅普诺夫稳定性判定定理有:

定义1[3]如果对任意给定的ε＞0，存在δ＞0，使得当任一x0∈Rn满足‖x0‖≤δ时，方程由初值条件x(t0)=x0确定的解x(t)，对一切t≥t0均有‖x(t)‖≤ε，此时方程的零解x=0 是稳定的，如图1 所示。

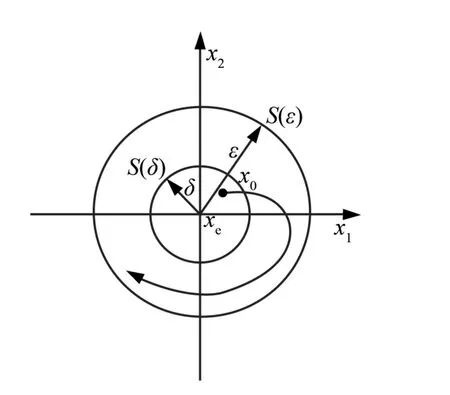
图1 稳定示意图

定义2[3]如果方程的零解是稳定的，并且存在δ0＞0 使得当‖x0‖＜δ0时，满足初值条件x(t0)=x0的解x(t) 均有则此时称零解x =0 是渐近稳定的，如图2 所示。

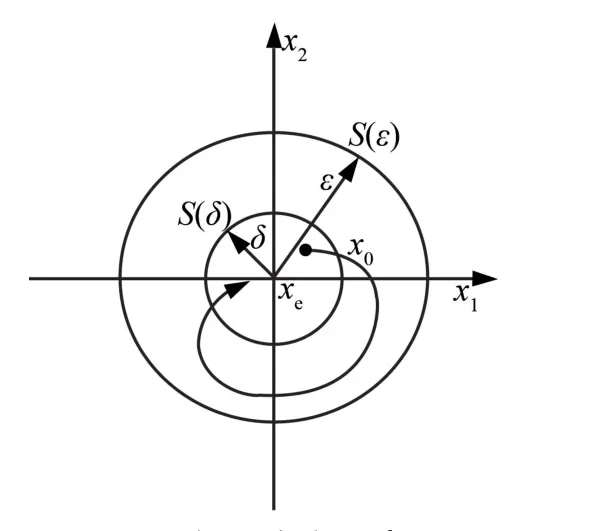
图2 渐近稳定示意图

定理1[3]如果式(1)可以找到一个正定函数V(x) ，其通过式(1)的全导数为常负函数或者等于零，则式(1)的零解是稳定的；

如果正定函数V(x) 通过方程组的全导数为定负的，则式(1)的零解是渐近稳定的；

如果存在函数V(x) 和某一非负常数μ，且通过式(1)的全导数可以由式(3)表示为

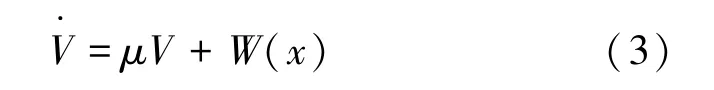
当μ =0 时，W为正定函数；当μ≠0 时，W为常正函数或者恒等于零，并且在x =0 的任意小邻域内至少存在某个，使得V()＞0，则式(1)的零解是不稳定的。

2 风机速度渐近跟踪控制的设计与分析

2.1 风机速度控制系统模型

文章将应用李雅普诺夫稳定性理论研究风机速度控制系统的速度渐近跟踪控制问题。 一类由直流电动机驱动的风机速度控制系统，其数学模型[11]由式(4)表示为

式中:v为风机转速，rad/s；y = v为系统的输出，rad/s；I为电枢电流，A；u0为输入电压，作为系统的控制输入，V；τD(v) 为不确定的转动负载，其依赖于风机速度；J1为转动惯量，kg·m2；J2为电感系数，H；R为电阻，Ω；k1、k2为已知比例常数。

在文献[11-15]中，将转动负载τD(v) 假定为风机速度v的线性函数并通过设计控制律使得系统的转速达到稳定状态。 文章在此基础上，进一步考虑在τD(v)= ωv3(ω为未知常数，ω＞0)为非线性函数情况下，将电机作为转矩源，通过反步法设计速度控制器，并利用李雅普诺夫稳定性理论证明风机转速v能够实现对任意给定速度vr的渐近跟踪控制并达到稳定状态。

2.2 风机速度渐近跟踪控制器设计

式(4)可转化为一类非线性微分方程并由式(5)表示为

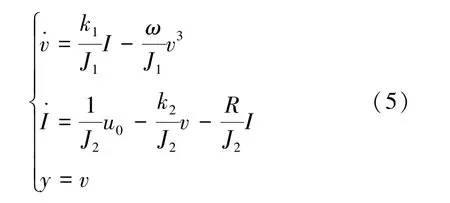
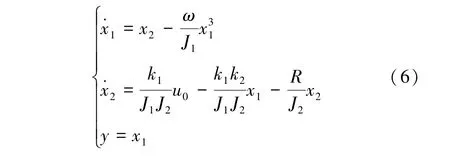
对于给定的任意速度设定值vr(t) ， 定义误差变量z1= x1- vr，通过选取连续可微的Lyapunov 函数设计速度控制器u使得误差z1在t→∞时趋于零。

步骤1: 针对式(7)，为应用反步法，选取α1为虚拟控制律，令误差为z2= x2- α1。 考虑李雅普诺夫函数根据式(7)，V1的时间导数可由式(8)表示为

因为ω未知，从而θ是未知常数，因此难以判断其负定性，采用自适应变量估计对θ进行补偿。假设是未知常数θ的在线估计值，是估计误差，则由式(8)得到的由式(9)表示为

选取虚拟控制律α1由式(10)表示为

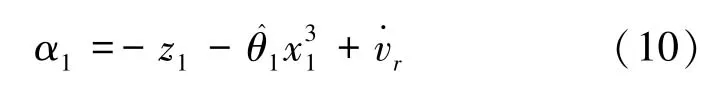
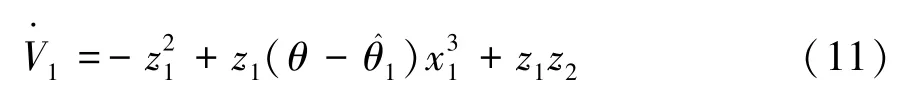
对式(12)求导，得到式(13)为

将式(14)代入式(13)，可得到式(15)为

步骤2:选取的李雅普诺夫函数，由式(16)表示为

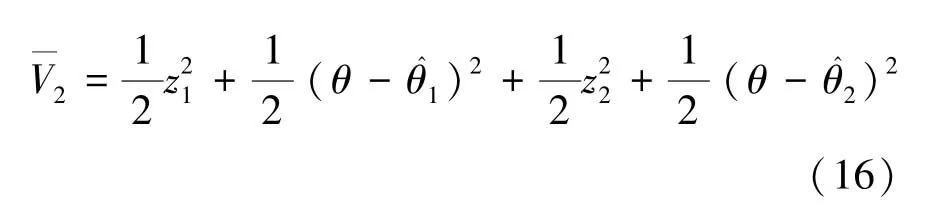
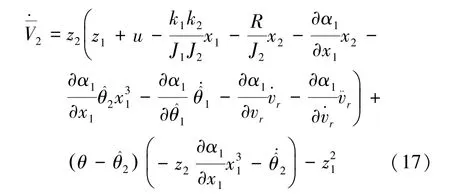
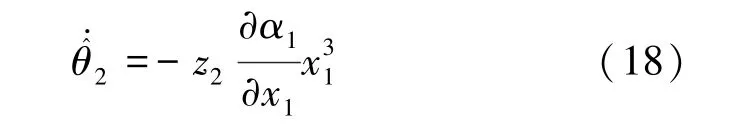
速度控制器u由式(19)表示为

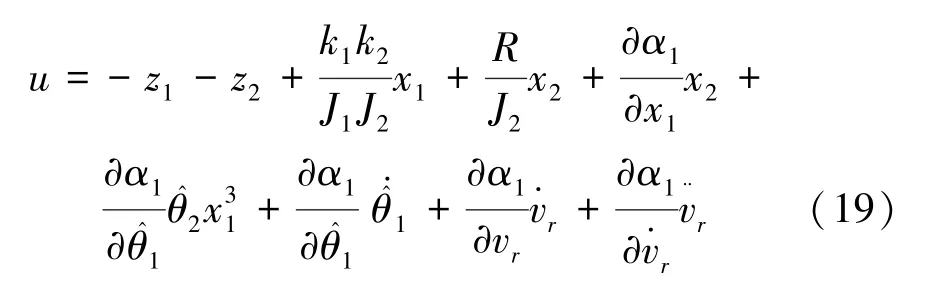
从而式(17)可化为式(20)表示为

2.3 风机速度渐近跟踪控制的稳定性分析

对于变换后的风机速度控制系统(4)，应用设计的自适应速度跟踪控制器(19)，得到闭环系统由式(21)表示为

式(21)即为非线性常微分方程组。 考虑到式(16)中选取的李雅普诺夫函数为正定连续可微函数，其导数满足式(20)，可知为常负函数，因此满足渐进稳定的条件，根据李雅普诺夫稳定性定理1 可知非线性微分方程式(21)的解是稳定的。

根据式(20)，对其两边积分得到式(22)为

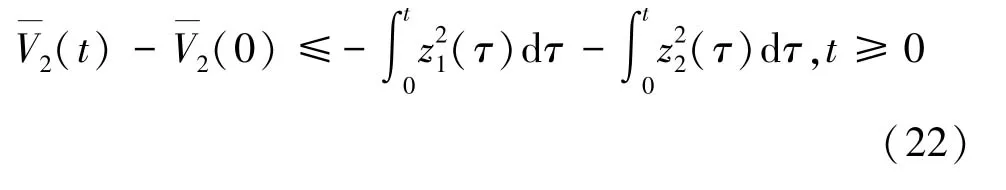
即可由式(23)表示为

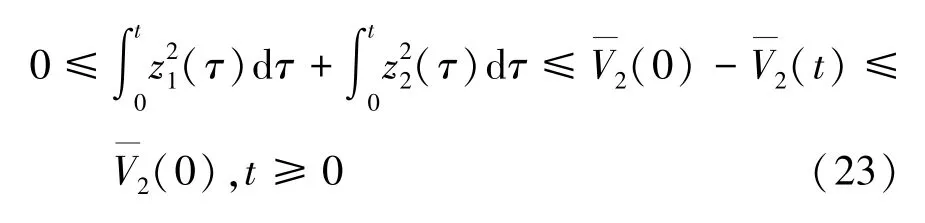
因此，z1、z2是平方可积的；考虑到有界且θ为(未知)常数，vr(t) 为已知有界函数，得到α1及有界，从而根据式(22)可知是有界的。 根据Barbalat 引理[17]，由式(24)表示为

考虑变换，变换矩阵由式(25)表示为

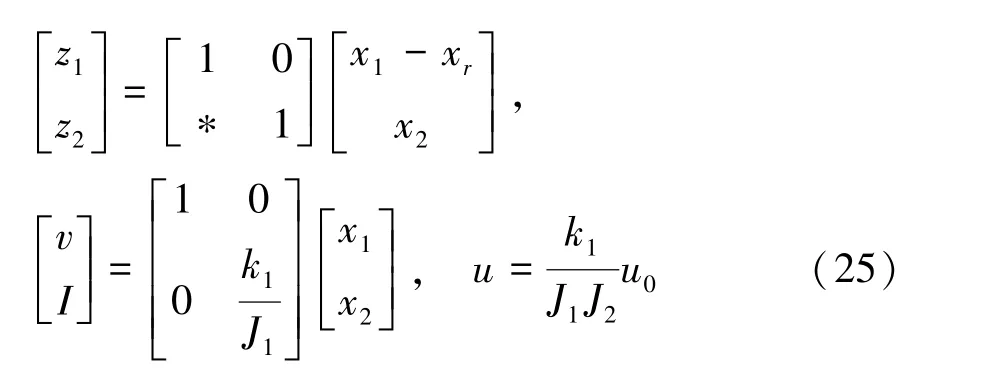
式中:*代表矩阵的某元素，显然其大小不影响矩阵的可逆性。

根据式(25)，上述变换矩阵满足条件由式(26)表示为

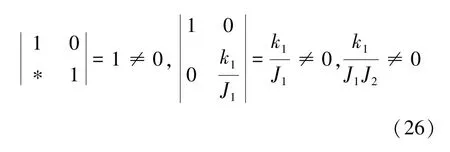
式(25)定义的变换是可逆的，因此设计的速度控制器能够实现风机速度的渐近设定点跟踪控制。

综合上述分析，可以得到如下结论:

对于风机速度控制系统，在转动负载为不确定非线性函数的情况下，应用文章中设计的速度控制器u，能够保证闭环系统的解(x1，x2，θ＾1，θ＾

2) 全局有界，且能够实现风机速度v(t) 对于任意给定的速度设定值vr(t) 的渐近跟踪控制，即由式(27)表示为

3 风机速度渐近跟踪控制的仿真实验

对提出的控制方案进行仿真实验，根据式(25)的逆变换，应用速度控制器u，可以得到风机速度控制闭环系统，由式(28)表示为

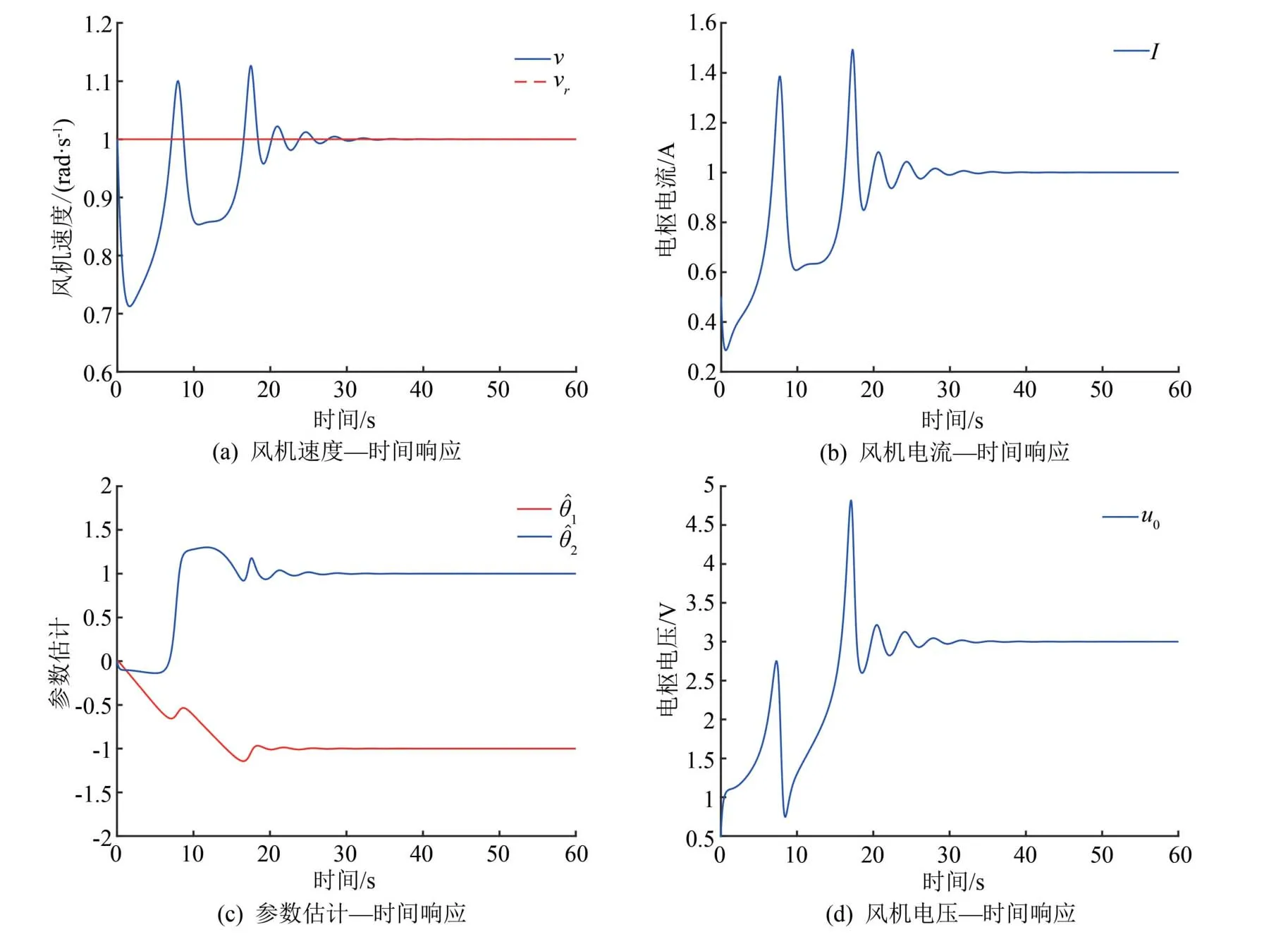
图3 设定速度vr = 1 时，风机系统及参数估计与时间的响应图

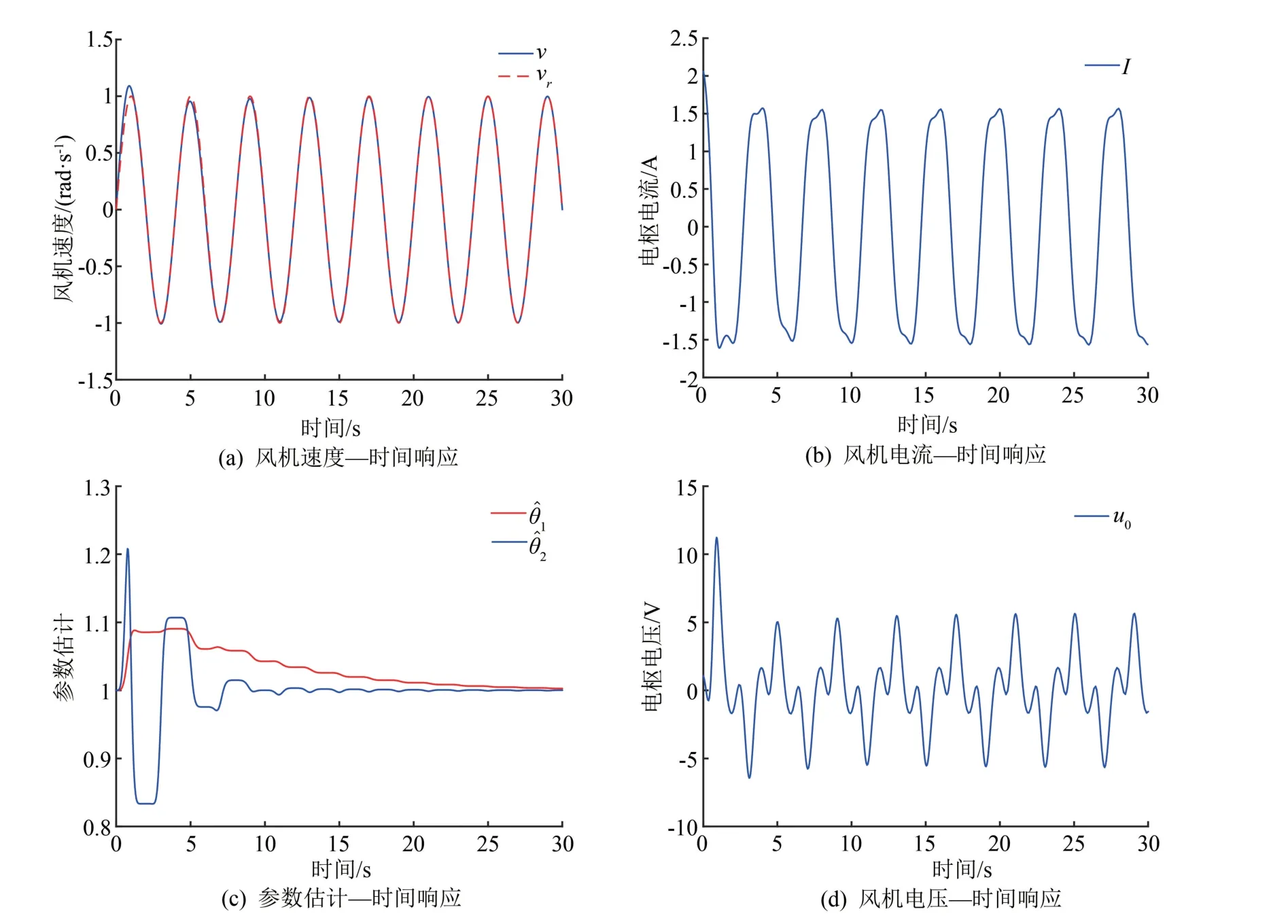
图4 设定速度vr=sin(0.5πt)时，风机系统及参数估计与时间的响应图

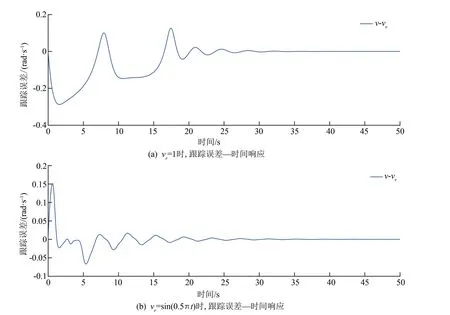
图5 风机系统在两种不同设定速度下跟踪误差与时间的响应图

由图3(a)、4(a)和5 仿真结果可知，在电机参数存在不确定性和转动负载为非线性函数的情况下，对于给定的设定速度为常数和正弦类时变函数，通过设计的输出电压可以使得风机转速达到设定速度并保持稳定状态。 由图3(b)和(d)可知，在设定速度vr =1 时，稳态电流和稳态输入电压分别稳定在常数I=1 和u=3。 由图4(b)和(d)可知，在设定速度vr =sin(0.5πt) 时，如同给定的正弦类设定速度，电流和输入电压亦是波动的周期时变信号，这一现象与实际情形相符合。 考虑到系统参数为未知的常数，图3(c)和4(c) 的仿真结果说明了估计值和稳态亦为常数。

4 结论

根据上述研究结果可得出以下几点结论:

(1) 针对一类转动负载为不确定非线性函数的风机速度控制系统，文章引入动态辅助变量对未知常数参数进行估计，应用反步法设计风机速度控制器，使得风机速度控制系统转化为非线性常微分方程组，利用李雅普诺夫稳定性理论证明了风机转速能够实现对任意给定速度的渐近跟踪控制并达到稳定状态。

(2) 风机速度渐近跟踪控制的Matlab 仿真结果验证了控制理论算法的有效性，并且提出的风机速度控制器方案对风机速度控制系统中存在的未知参数具有良好的稳定性。