一类非线性波动方程的孤波解
杨 洁, 肖 冰, 张 宁
(新疆师范大学数学科学学院,乌鲁木齐 830017)
随着科学技术的发展,越来越多的复杂问题都可以用非线性偏微分方程来描述,例如在流体力学、等离子物理学、光电通信、固态物理学以及交通等领域应用广泛. 但是由于线性微分方程的一些基本性质在非线性微分方程中不再成立,很难用一个统一的方法来求解后者,所以长期以来,求解非线性偏微分方程的精确解一直是数学家和物理学家研究的热点问题[1-3].
目前已发现越来越多的具有重要物理意义的非线性偏微分方程,如Korteweg-deVries方程、Huxley方程、Fitzhugh-Nagumo方程等都具有各种类型的孤立波解[4-5]. 孤立子正在流体物理学、基本粒子物理学、生物医学等许多领域找到了应用,并对一些过去难以解释的现象做了说明. 随着孤立子理论的发展,人们提出了许多求解非线性偏微分方程的有效方法,如齐次平衡法[6]、G/G′展开法[7]、双曲正切函数展开法[8]、Jacobi椭圆函数展开法[9]、试探函数法[10]等一系列的方法.
最近,王明亮等[11]用齐次平衡法求出了一个1+1维非线性波动方程
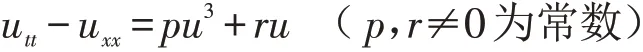
的精确解. 张卫国[12]用待定系数法求出了非线性波动方程
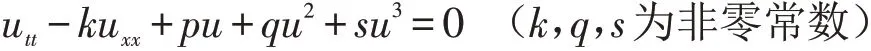
的钟状和扭状孤波解. 范恩贵等[13]用齐次平衡法求出了一类非线性波动方程
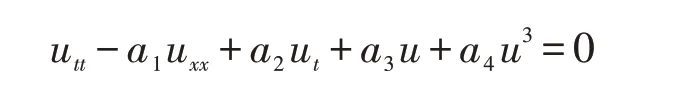
的孤立波解. 尚亚东[14]用结合假设方法求出了非线性波动方程

的一些显式精确行波解.
基于他们的研究,本文利用最近引入的首次积分法的思想[15-16],来求解如下一类应用较广泛的非线性波动方程

的孤波解,其中a1,a2,a3,a4,a5均为方程参数. 求解方程(1)的孤波解具有非常重要的意义,因为物理学上的一些比较重要的方程,如φ4方程、Duffing方程、Sine-Gordon方程的近似方程、Sinh-Gordon方程的近似方程、Landau-Ginzburg-Higgs方程、Klein-Gordon方程以及非线性电报方程等都可以看作是该方程的特殊情形.
1 研究方法
考虑非线性偏微分方程

设u(x,t)是方程(2)的解,对方程(2)作行波变换u(x,t)=u(ξ),其中ξ=x-vt,则方程(2)可转化为常微分方程

现引入新的变量X(ξ)=u(ξ),Y=uξ(ξ),则可以得到常微分方程组:

其中:F是关于Y的导数表达式;v为液速.
接下来利用Division 定理来得到式(4)的一个首次积分,从而可以把方程(3)化为一阶可积的常微分方程,通过解这个方程可以得到方程(2)的解,其中Division定理如下.
Division 定理[17]假设P(w,z),Q(w,z)是复数域C[w,z]上的多项式,并且P(w,z)是复数域C[w,z]上的不可约多项式,如果P(w,z)的所有零点也是Q(w,z)的零点,那么在复数域上存在一个多项式G[w,z]使得Q[w,z]=P[w,z]G[w,z] .
2 非线性波动方程的孤波解
现在利用首次积分法来求解非线性波动方程(1)的孤波解,作行波变换

其中:v是波速. 通过行波变换式(5)可以将方程(1)化为常微分方程:

令X(ξ)=u(ξ),Y=uξ(ξ),则方程(6)等价于
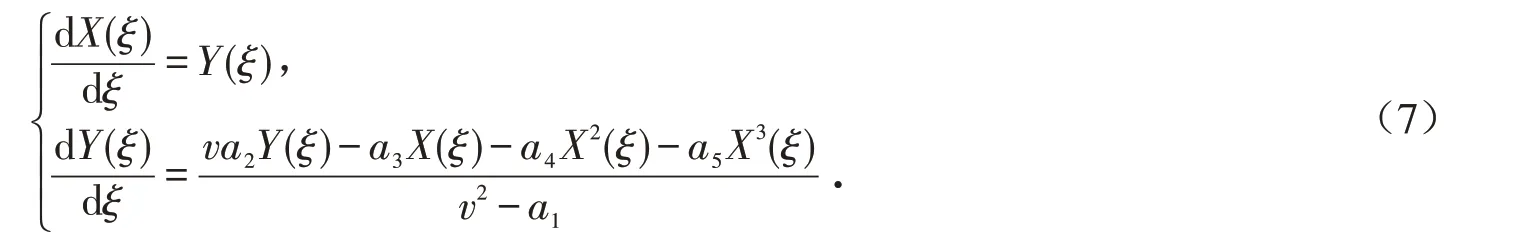

由式(16)以及方程(7)可得

解常微分方程(17)可以得到方程(1)的解为:

其中:C1为任意常数.
特别地,当a4=0 时可以得到非线性电报方程

的两个孤波解为:

注1如果取a1=2,a2=-2,a5=1,v=1,C1= 2,可以得到非线性电报方程(20)的特解为:
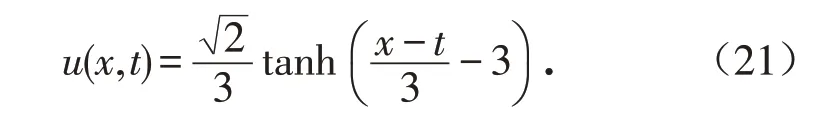
利用MATLAB做出其图形,如图1所示.

图1 方程(20)的特解的图像Fig.1 Graph of the particular solution of equation(20)
3 结论
在本文中,利用首次积分法,获得了一类含有多个任意参数的非线性波动方程的孤波解,同时当参数取不同的特殊值时,对应地可以获得不同的孤波解. 更值得注意的是,本文所研究的方程包含了数学物理中的一大类非常重要的非线性数学物理方程.本文中所获得的精确解或许对于这些方程在物理上的应用将会有一定的实际意义.

