一类对称型不等式的一种证法

李居之

(河南省南阳师范学院软件学院,473061)

对于对称型不等式,比较常见的方法就是构造局部不等式来证明.但在面对不同的不等式问题时,如何来构造局部不等式却是比较难处理的.本文从一类条件为“abcd=1”的四元分式型的对称不等式着手,通过引入、控制待定系数,最后将其统一构造出一个熟知的局部不等式来证明.

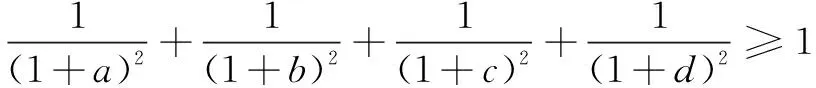
这里,给出一个熟知的简单证明.

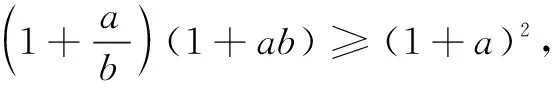
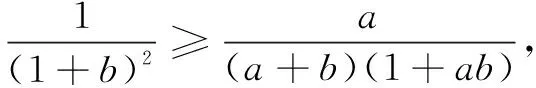
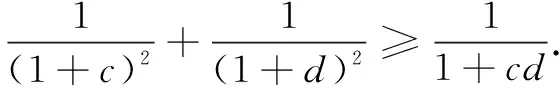
下面举几个例子,来应用这个结论.

证明当x>0时,有

⟺t10-t8-t6+2t5-t4-t2+1≥0

⟺(t-1)2(t2+t+1)(t6+t5+t3+t+1)

≥0,显然成立.

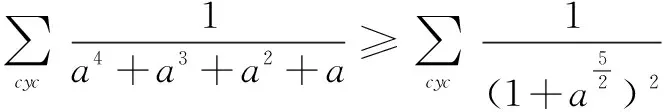
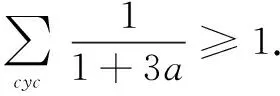
证明当x>0时,有

⟺t6-3t4+2t3≥0

⟺t3(t+2)(t-1)2≥0,显然成立.

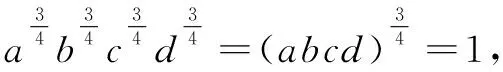
评注此题改编于2004年吉林省竞赛题、2004年德国数学奥林匹克选拔考试题:已知正数a,b,c,满足abc=1,求证:

例3(Mathematical Reflections J500)已知正数a,b,c,d满足abcd=1,求证:

证明当x>0时,有

5x2-2x+1≤(1+x2)2

⟺x4-3x2+2x≥0

⟺x(x+2)(x-1)2≥0,显然成立.

又因为a2b2c2d2=(abcd)2=1,由上面的结论知所证不等式成立.

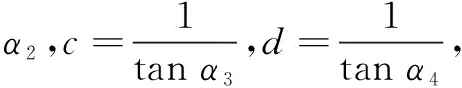
证明当x>0时,有

⟺(x3+2)(x12+3)≥3x(x3+1)2

⟺x15+2x12-3x7-6x4+3x3-3x+6

≥0

⟺(x-1)2(x13+2x12+3x11+6x10+9x9+

12x8+15x7+18x6+18x5+18x4+

18x3+12x2+9x+6)≥0,显然成立.

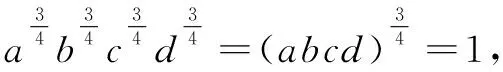
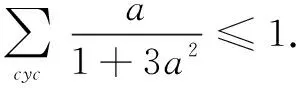
另外,利用均值不等式可将此不等式转化到例2.这说明此不等式是比较弱的.

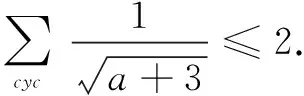
证明当x>0时,有

⟺4(x8+3)(2x3+1)2≥9(x3+1)4

⟺4(16x14-9x12+16x11-36x9+4x8-

6x6+12x3+3)≥0

⟺(x-1)2(16x12+32x11+39x10+62x9+

哀乐又一次响起在这屋里，阿东被这悲哀之声压迫得透不过气。但阿里却立即把头伸出被子。他的脸上露出平静表情。仿佛真的是在听母亲的声音。他不说话，只侧耳倾听。

85x8+72x7+63x6+54x5+39x4+

24x3+9x2+6x+3)≥0,显然成立.

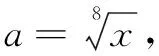
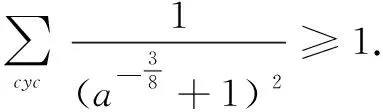
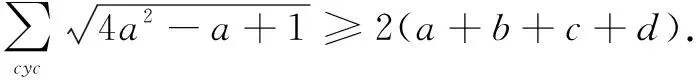
证明当x>0时，有

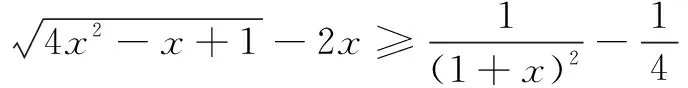
⟺16(4x2-x+1)(1+x)4≥(8x3+

15x2+6x+3)2

⟺15x4-4x3-30x2+12x+7≥0

⟺(3x+1)(5x+7)(x-1)2≥0,显然成立.

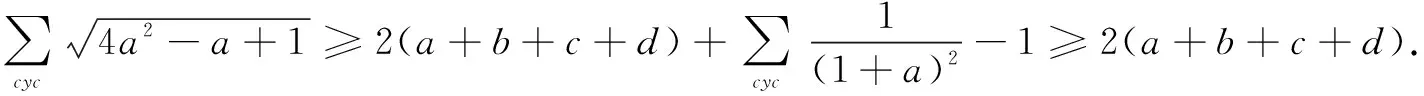
证明当x>0时，有

⟺4x(3+x4)≥(8x-x4-3)(1+x)2

⟺x6+6x5+x4-8x3-13x2+10x+3

≥0

⟺(x-1)2(x4+8x3+16x2+16x+3)

≥0,

显然成立.

需要说明的是,这种方法有一定的局限性,甚至在使用起来时并没有其他的方法简单.尤其是对于待定系数的控制,读者朋友们稍不留意,就有可能陷入其中.但当面对这一类对称型不等式束手无措时,不妨尝试拿来应用,有时也不失为一种好方法!