“陷阱”式教学法在经管类微积分教学中的应用
(南京财经大学应用数学学院,江苏 南京210023)
1 引言
微积分作为经管类本科专业的一门的重要基础课,不仅为后续专业课学习提供了必要的知识,而且为培养学生的逻辑思维能力、分析及解决实际问题的能力奠定必要的基础[1]。因此,微积分学习的好坏将直接影响到后续各专业课的学习效果以及学生继续深造的积极性。但如今受到教学大纲的整体学时以及教学工作者对微积分教学存在的片面认识等影响,使微积分的教学效果及改革步履维艰[2]。具体表现在:首先,在教学内容上,不仅与高中数学知识存在一定的脱钩,而且一些教学工作者对教学理念和方法存在固步自封的情形,严重影响经管类高等教育改革的步伐和相应的人才培养的需要[3];其次,由于微积分的逻辑性、抽象性强,学习起来相对枯燥无味,从而导致一些学生放弃学习;一些爱好数学的学生,由于初期学习对一些抽象概念、性质以及定理理解不够深刻,加之学而不精、学而不用,导致学习效果不佳。这些客观原因的存在,都反映出微积分教学方法和教学理念改革的迫切性。
为了提高经管类微积分的教学效果,更好地为后续专业课程服务,本文提出了一种基于“陷阱”式的教学法,探讨经管类微积分课程的教学改革。实践表明,该方法能够有效地提高学生对微积分中的抽象概念、性质以及定理的理解程度,提高其学习积极性,增强其专业的应用能力。
2 “陷阱”教学法的具体应用实例
2.1 在抽象概念中的应用
微积分中的一些抽象概念由于课时以及大纲要求等限制,导致学生对这些抽象概念理解不准确,甚至糊里糊涂。为了加深学生对这些抽象概念的理解深度,特引入“陷阱”式教学法。
例如:无穷大量和无界变量的概念在微积分的学习中扮演着非常重要的作用,特别是在极限运算中的作用尤为明显。由于无界变量是对整个定义域而言,而无穷大量则是对极限趋势来说的。在实际教学中,教师一般是在不同教学时段来进行讲解这两个概念,从而导致大部分学生对两者的概念容易产生混淆,甚至把两者混为一谈。本文通过引入“陷阱”式教学案例,将两者有机的结合在一起进行讲解,让学生更加深刻的理解无穷大量和无界变量的概念。
例1:判断函数f(x)=xsin x在整个实数域上是无穷大量还是无界变量。
解:首先通过如下的方式使学生掉进无穷大量的“陷阱”之中,即令 x=2nπ+π/2 时,则所以f(x)是无穷大量。而后给学生分析正确结果如下:该函数是偶函数,故只需关注 x∈[0,+∞),当 x取 nπ 时,则,所以f(x)不是无穷大量,但既然有一个子列可以使xsinx→∞,故f(x)无界变量。
例 2:判断数列 an=[1+(-1)n]n2是无界变量还是无穷大变量。
解:首先使学生生搬硬套概念公式,即n2是无穷大量,1+(-1)n是常数,使其掉进错误的 “陷阱”里,即数列 an=[1+(-1)n]n2是无穷大变量。 然后给学生分析正确结果如下:因为a1=0,a2=4,a3=0,a4=8,L,a2n-1=0,a2n=4n,L 显然数列 {an}是无界的,又因为,所以数列{an}不是无穷大。
通过以上两个“陷阱”式教学案例,可以使学生更加深刻理解无穷大量和无界变量的概念,并能够准确判断它们之间的关系,即无穷大量一定是无界变量,反之无界变量不一定是无穷大量,从而有助于提高学生学习微积分概念的兴趣,让其感受到微积分中抽象概念的魅力所在。
2.2 在具体性质中的应用
微积分中一些抽象的性质,同样由于客观原因限制,在授课的过程中,其理论证明过程往往是省略的,从而导致一些学生只会机械地使用。特别是在不满足性质条件的情况下,如果继续生搬硬套该性质,最终将得到错误的结果。
幂指函数在同济版《高等数学》[4]中给出其一般形式是 f(x)=u(x)v(x)并 u(x)>0 且,掌握其求极限的方法是微积分教学中的一个重要内容,教材上一般都是直接给出其公式如下:
设 lim u(x)=A>0,lim v(x)=B,则有
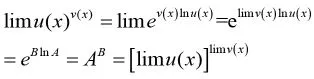
上述幂指函数的极限公式,使得本来一个复杂的函数极限问题转化为分别求简单的底函数u(x)和指函数v(x)的极限,然后对其极限进行幂运算的问题。但往往容易忽略幂指函数极限公式成立的先决条件为:函数u(x)和v(x)的极限存在且u(x)的极限大于零,想当然的生搬硬套幂指函数的求极限公式。
例3[5]:求
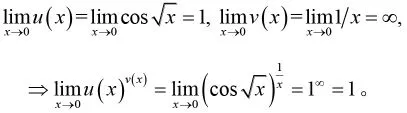
其次引入一个重要的极限反例,
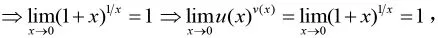
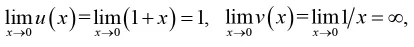
使学生意识到掉进了一个错误的陷阱之中。最后,给学生讲解正确的幂指函数求极限公式,设

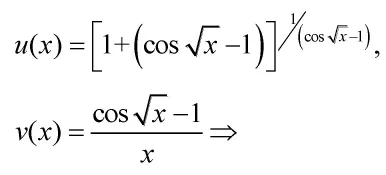
上述“陷阱”式教学案例可以使学生深刻的认识到幂指函数求极限法则的使用条件为:底函数u(x)和指函数v(x)的极限首先都要存在,而不是分别求底函数u(x)和指函数v(x)的极限,然后对其极限进行幂运算。
此外,学生在幂指函数求极限问题中,比较容易错误的第二种情况为:A=∞,B=0,=AB=∞0=1。我们同样可以通过引入文[6]中的具体例子来设置“陷阱”式教学案例,帮助学生进一步理解和熟练运用幂指函数求极限法则。
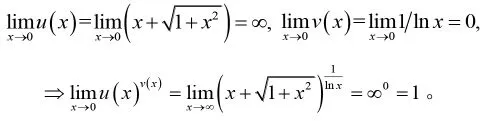
而后给学生分析正确的计算结果如下:
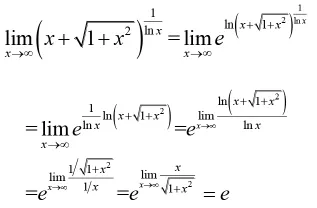
通过上述两种情形的“陷阱”式教学案例,即“A=1,B=∞”和“A=∞,B=0”情形,能够使学生在以后的学习中更加牢记并深刻的理解幂指函数求极限的法则。
2.3 在具体定理中的应用
考虑到教学大纲以及教学学时等客观因素影响,教师在实际教学中对微积分中一些重要定理往往不给出详细的理论证明,而仅仅讲解如何有效地运用这些定理去解决问题。因此,往往会导致学生只会机械地使用这些定理,而对定理的实际含义一知半解,以至于在一些具体的运用中,缺少一些关键元素,导致定理的误用。
例如:不定积分在微积分的教学中起到非常重要的作用,对后续定积分学习的好坏起到决定性的作用,而大多数同学对不定积分的定理一知半解。其中,容易出现的错误情况是把不定积分等同于求函数的原函数,从而在计算结果中缺少一个关键的元素常数C。我们可以通过引入如下“陷阱”式教学方案,使学生能够深刻的理解不定积分的实际含义并能够在实际应用中牢记在等式的后面加上常数C。
例6:求不定积分

通过这个“陷阱”式教学案例,可以首先让学生掉进误以为自己算错的“陷阱”之中。然后我们通过如下方式给学生解释上述两个不定积分为什么都有两种正确结果,从而使学生更加深刻理解到不定积分后面的常数C的重要意义。
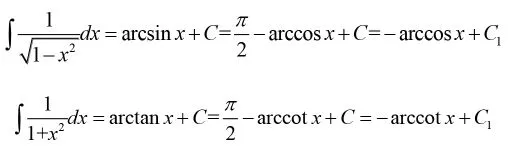
例7:求不定积分
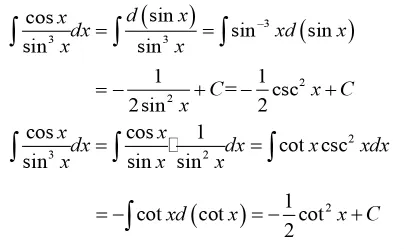
同样通过这个“陷阱”式教学案例,首先可以让学生掉进以为是自己算错的“陷阱”之中;然后利用三角函数的恒等式关系给出正确的结果,让学生明白两种计算结果不一样是由于忽略了不定积分后面的常数C的缘故;最后可以使学生更加深刻理解并认识到不定积分常数C的重要意义。
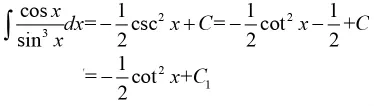
3 结束语
经管类微积分的教学改革是一项任重道远的任务,在国家强力推行素质教育的今天,也应该随着教学理念的革新以及教学手段的进步,不断推陈出新。同时,教育主管部门也应更加重视基础学科的建设,对微积分等数学课程给予更多倾斜[7]。本文探讨了如何通过引入“陷阱”式教学案例,加深学生对微积分中抽象概念、性质以及定理的理解,以达到提高教学效果的目的。但在实际教学中,教师在引入“陷阱”式教学案例时,还应该根据实际知识的特点,有机地将“陷阱”式教学法引入到微积分教学中,不能东施效颦式的使用“陷阱”式教学法,其结果必然适得其反。

