定理公式之来源 高三复习之根本

王平 彭飞

[摘  要] 当前高三复习定理公式时，大都是定理公式一遍过，各种题型冲上来，看似有效，实则并没有能提高学生对知识内涵与本质的理解.解决问题时，往往靠的是记忆与模仿. 定理公式的产生过程，是顶层设计的思维过程，是对问题本质方法的思维过程，为学习者提供了解决问题的宏观思路与突破方向，故高三复习时不仅仅要注重定理公式结论性知识，更要注重对定理公式产生过程的复习.

[关键词] 定理;公式;本质;提升;深度学习

抛出问题

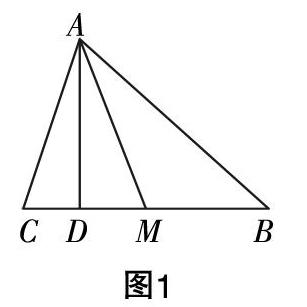
例题：在△ABC，已知角A，B，C所对应的边分别为a，b，c，且满足2bsinC+■=a+c.

（1）求角B的大小;

（2）若M为BC的中点，且AM=AC，求sin∠BAC的值.

本题为正弦定理复习教案中的一道习题，第（1）问的复习功能侧重于对基本知识、方法的运用与理解，核心思想方法为边转化为角的思想方法，学生是可以轻松地将条件中的边转化为角的正弦，整理变换之后，可以得出B=■.学生在预习第（2）个小问题后，感觉特别难，有一种虽熟知了正弦定理公式，多次运用公式，但很无奈，无从下手的感觉.

笔者对此题进行了仔细的评讲，讲解过程如下，作出了MC的中垂线AD（如图1），设CD=x，则MD=x，BM=2x，所以得到AB=6x，由勾股定理可以得到AD=3■x.

在Rt△ADC中，由勾股定理得到：AC=2■x.

在△ABC中，由正弦定理得到，■=■，得到sin∠BAC=■.

讲解过程似乎很顺利，然而下课后，一个学生跑过来，弱弱地问了一句：“老师，我怎么就想不到作这条垂线，你是怎么想到的呢？”

高三复习定理的现状

由于高三的定理公式等知识都是学生学习过的，学生对此已经有了一定的认知基础，故高三复习时，大都数教师都会采用一般到特殊的复习方式，即为先对定理进行笼统的复习. 如正弦定理，先复习正弦定理的内容，再复习正弦定理产生的变式定理，然后给出几个注意点，定理内容在不超过10分钟的情况下基本复习结束.接下来便是不断做题，总结运用定理公式的方法，遇到没有思路的问题，大都是教师先点拨，打开思路，然后解决问题. 可惜的是，由于高三复习的紧张、时间的限制等等，教师的点拨往往演变为直接告知学生，即便是引导，也会呈现出“诱导”的特征.

上述问题中，作出中垂线AD过程，显然是笔者直接告知，笔者认为学生应该有能力作出辅助线，实则不然;倘若教师了解了学情，注重了课堂引导，对学生的学习应该有一定的帮助作用，但终究敌不过学生自己生成解决方法来得好.那么作为教师，我们应该如何去组织复习，才能让学生自我生成解题的方法呢？首先要解决的第一个问题就是，学生为什么想不到这个辅助线. 这个问题说明，我们对定理公式的复习工作具有一定的局限性.在高三复习过程中，我们往往注重的是定理公式的结论性知识复习，没有抓住定理公式的产生过程进行复习，这样学生往往关注的就是公式的套用，不注重定理公式发生发展的学习，就更谈不上思维品质的提升. 下面笔者就以复习正弦定理（苏教版）为例，谈谈定理公式复习的一些想法.

复习定理来源 提升思维品质

苏教版教材提供了正弦定理的四种证明方式，那么这四种证明对高三复习都起到了哪些作用呢？又提升了学生哪些品质呢？

1. 培养学生“斜化直”的思想

教材提供的第1种证法是，由直角三角形猜想出正弦定理，然后由猜想推广到一般三角形，继而给出证明. 证明过程就是想办法将斜三角形转化为直角三角形来求证，出于对三角形形状的考虑，需要分三种情况讨论，从而得出正弦定理的一般性. 证明正弦定理的这一方法，其实为学习者提供了解决斜三角形的方法，那就是斜三角形可以转化为直角三角形来解决问题. 这种方法可以归结为“斜化直”的思路，上述例题，学生之所以想不到作垂线，就是因为“斜化直”的思想没有形成，也就导致问题不能得以解决. 通过对正弦定理方法1的复习，很好地培养了学生解决斜三角形的一般途径，提升了学生转化与化归的能力，提升了学生的思维品质.

2. 培养学生的轨迹意识

正弦定理证明的第2种方法是借助三角形的外接圆来证明的，是怎么想到这一方法的呢？根据第1种方法可知，斜三角形的问题是通过直角三角形来解决，而直徑所对的圆周角为直角，从而联想到构造三角形的外接圆. 在外接圆内，根据题意需要，反复利用不同的直径构造直角三角形，将原三角形中的边和角转化到直角三角形中解决. 复习解法2后，首先，根据证明正弦定理最初的想法——构造直角，这能帮助学生想到构造垂直，解决上述例题. 其次，第2种方法需要多次构造不同的直角三角形，为什么可以多次构造呢？因为直角顶点始终在外接圆上，其本质是轨迹思想.利用轨迹思想，我们可以优化解决不少的数学问题. 如：满足条件：AB=2，AC=■BC的△ABC的面积的最大值.本题若是通过解三角形的方法求解，则难度很大，然而由条件可知AB是定值，点C是动点，不禁联想到去寻找出点C的轨迹，通过求解，得到原来点C的轨迹是一个圆. 此时，△ABC面积的最大值不费吹灰之力，迎刃而解. 通过对正弦定理方法2的复习，很好地培养学生的轨迹意识，提升学生动态处理问题的思维.

3. 培养数学工具性的意识

正弦定理的第3种方法为利用了向量方法求证，先看看具体的证明过程.在△ABC中，有■=■+■. 不妨设∠C为最大角，过点A作AD⊥BC于D（如图2），于是■·■=（■+■）·■=■·■+■·■，即0=■·■cos（90°+B）+■·■cos∠DAC，其中当∠C为锐角或直角时，∠DAC=90°-C;当∠C为钝角时，∠DAC=C-90°，故可得正弦定理.首先，这样的证明方法也涉及转化到直角的角度上来，复习了这样的方法，也可以帮助学生想到解决上述例题的途径. 其次，向量有方向（角度）、模（长度）两个要素，而三角形的边角关系，恰好涉及三角形的内角及边长两个量，并且在向量的运算中又正好有一个三角形法则，这些特征自然而然地显示出它们之间可能存在某种内在联系[1]. 这种方法其本质说明了向量是解决几何问题很好的工具. 比如：已知在△ABC中，A=120°，AB=4，若点D在边BC上，且D为BC边上靠近C点的三等分点，AD=■，求AC的长度. 本题是解三角形问题，学生往往容易想到利用正弦、余弦定理解决问题，但是利用正弦、余弦定理解决时，却有力不从心之感. 但我们借助向量可以迅速地找到解决的方案，将■，■作为基向量，来表示向量■，即■=■■+■■，然后对此式两边平方，即可得到关于■的方程，一下子解决问题.数学本身就是解决实际问题的工具，向量则是我们工具中的工具，这种方法培养学生的工具意识，提升了学生的核心素养.

4. 培养几何问题代数化的意识

正弦定理证明的第4种方法，建立直角坐标系，同时配合运用三角函数的定义、等积法等思路证明了正弦定理，将几何问题代数化，这种方法也是我们解决几何问题的一般解法，这样的方法深入人心，培养学生用精确的代数计算解决几何问题，很好地培养了学生数形结合的思想. 有了这样的思维意识，上述例题的垂线也能如约而至.在我们平时解题时，也会经常遇到此类问题. 如：江苏省2018年高考试题的第13题，在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1（如图3），求4a+c的最小值.本题从题面上看，是一道解平面几何问题，但求解的目标恰是代数问题，故我们可以将几何问题代数化，以B为原点，BC所在的直线为x轴建立平面直角坐标系，则D■，■，C（a，0），A-■，■，由A，D，C三点共线，可知kDC=kAC，整理得ac=a+c，即■+■=1，此时一道几何问题就轻松地转化成了基本不等式问题，运用“1”的代换就可以解得4a+c的最小值了.高三复习重在通性通法的学习，这样的方法是解决几何问题的一般解法，具有普遍性，在宏观层面上对学生起到了一定的指导意义.

5. 培养学生方程组意识

当然，正弦定理证明过程是利用已学知识得出三角形中边角的关系，不论有多少种方法，但其目标都是一样的，寻求边角关系，这就为我们解决三角形问题提供了宏观层面的思路.就上述问题而言，要求出目标角∠BAC的正弦，我们可以先求其余弦值，而余弦值的求解，只需要知道三角形三边的比例关系就可以了，如何突破呢？题中已经给出了∠B的值，由于∠B在△ABC和△ABM两个不同的三角形内，利用余弦定理，则可以得到含有三個未知数的两个方程，将其中一个看作为已知的，其他两个就可以用已知的量表示了，从而得出三条边的关系，最后借助余弦定理和同角关系即可解决问题.

由此可以看出，定理的复习，不能仅仅局限于复习定理本身的知识，更有必要复习定理的证明过程，在复习完定理的证明过程后，本题的思路也就会自然而然打开，对几何问题的处理办法也就不仅仅停留在几何层面上，会获得更为宽广、更深刻的解法.

定理公式应如何复习

1. 关注知识结构，轻松解决试题

定理公式的结论性知识是四基之一的基本知识，它是高考考查的内容，高三复习过程中当然首先要重视学生对结论性知识的理解性识记、基本的运用等等. 例如：2011年陕西省（理科）第18题：叙述并证明余弦定理. 2011年的陕西省高考试卷中直接将余弦定理作为试题，进行考查，如果记不住定理内容，何谈去进行证明呢？其次高考中有占比不小的题是基础题，这些基础题，往往就是对结论性知识的基本运用.第三，认识与理解公式的结构，解决问题时更为轻松与巧妙. 如：已知在平面直角坐标系中（如图4），点A（2■，0），若直线l：■x+y+a=0上存在点P，使得∠OPA=60°，求实数a的取值范围. 本题观察已知条件可发现，在△OPA中，OA=2■，∠OPA=60°，很明显具有了正弦定理中边角相对的结构形式，从而可以得到点P在△OPA的外接圆上运动，此时通过借助轨迹思想，便可轻松地解决本题.所以高三复习时，教师要注重复习课本中定理公式的结论性知识，帮助学生复习定理公式的结构形式，复习它们的常规运用，以及其他需要注意的问题.

2. 关注证明过程，拓宽解题思路

定理公式的复习，一定要注重复习其证明的过程. 写进教科书的定理公式是前人对经验的总结，具有深远的影响.一个具有深远影响的公式，不能只仅仅关注公式定理本身的结构形式，更要注重定理公式的产生、发展过程，这样的过程，它会带给我们更多的启发. 如上述正弦定理的证明过程，它的意义远远大于定理本身，它的证明过程，给我们的教学提供了不少的宏观思想，给我们的学生提供了更宽泛的解题思路，拓宽了解题的视野. 如在解决三角形问题时，学生则不是一以贯之采用正弦、余弦定理，而是站在一个更高的角度来看问题，可以视这样的解三角形问题为三角形问题，也可以是向量问题，也可以是平面几何问题等等，有了这样的认知高度，就可以产生多种多样的方法，如：“斜化直”“向量工具法”“几何问题通过建系实现代数化”等等宏观层面的思路. 复习定理公式的证明过程比定理公式本身更为重要. 除了正弦定理之外，还有余弦定理、等差、等比数列的前n项和公式等等，都能为我们的解题提供更为宽泛的解决途径. 教材提供的解法也具有普遍的推广意义，为学生终身发展提供服务. 高考中有占比不小的题是能力题，这些题往往就是对思维方法的考查，体现解决问题的宏观途径与能力. 此时，仅仅考生掌握了结论性知识的结构和常规的运用方法显然不够，还需要对思想方法有更为深刻的认识，由此才能获取更高的成绩，思维层次才能更上一个台阶.

3. 关注过程优化，深度课堂教学

点到直线的距离公式是高三复习的重点知识，既要关注结论性知识，也要关注公式的产生过程. 已知点P（x0，y0），直线l：Ax+By+C=0，求点P到直线l的距离公式. 解决该问题的思路很多，苏教版课本中给出了两种不同的解法，等面积法和交点法. 其中交点法，课本在举了一个特例后，这样写道，这一方法运算量较大，言外之意就是这种方法不宜采用. 那真的是运算量大吗？该方法的解题过程为：过点P（x0，y0）解出l的垂线l′：Bx-Ay+Ay0-Bx0=0，然后由l与l′的方程，解出两直线的交点Q■，■，则PQ的长度d=■，即为点到直线的距离公式.从中我们可以看出，有一个特点就是思维量小，考试时，有些学生经常会因为思维不畅通，导致解题出现卡壳的现象. 如若在解题中，这部分学生选择思维量较小的方法，此时或许计算量较大，但只要一步一个脚印地运算下去，就应该是能获得部分成功的，因为总比无计可施要好很多. 当然在高三复习时，笔者认为还是有必要组织学生来进行运算，正是因为运算量大，才能暴露学生的运算问题，才能为我们深度的教与学提供素材. 同时组织学生运算的过程也是增强学生运算能力的过程，是培养学生数学运算素养的过程.

上述证明过程正是由于出现了运算量较大的问题，才给学生提供了深度学习的机会. 深度学习是相对浅层学习而言的，是以学习者主动参与为前提，以领悟内涵和抓住本质的深层思维为特征的一种学习方式和状态，是一种真实的学习过程，是一种高效的学习方式[2]■. 复习时，教师要有意识地引导学生对运算进行优化处理，即引导学生优化最难的运算部分——求两直线的交点以及两点间的距离. 如何优化呢？首先要有目标转化意识，求点到直线的距离，可以转化为点与直线上一点间的最短距离. 设直线l：Ax+By+C=0上一点Q′（x1，y1），则此时问题就可以转化为求PQ′的最小值，当Q′为l与l′的交点时，PQ′最小. 因为Q′为l与l′的交点，故满足Ax+By+C=0，Bx-Ay+Ay■-Bx■=0.将Q′（x■，y■）代入得到Ax■+By■+C=0，Bx■-Ay■+Ay■-Bx■=0（1），此时我们的目标为PQ′=■，从目标可以看出，Q′（x■，y■）是不可解出的，就需要将x■-x■和y■-y■看成兩个整体，故可以将（1）式改造为Ax■-Ax■+By■-By■=-Ax■-By■-C，Bx■-Ay■+Ay■-Bx■=0（2），对（2）继续向目标改进A（x■-x■）+B（y■-y■）=-Ax■-By■-C，B（x■-x■）+A（y■-y■）=0，将x■-x■和y■-y■看成两个未知数，解方程组可得x■-x■=■×（-Ax■-By■-C），y■-y■=■（x■-x■），代入目标形式，即得PQ′=■=■=■.

基于上述正弦定理的复习，几何问题还可以借助向量工具来解决. 由此，教师可以引导学生对本问题进行更为深度的学习. 设上述问题中的直线l与垂线l′的交点为Q（x■，y■），通过计算可以得到直线l的法向量是n=（A，B），■垂直于直线l，所以■∥n，故■·n=■·n，所以■=■=■. 又因为点Q（x■，y■）在直线l上，即Ax■+By■+C=0，所以■=■=■.

经过思维重组，适当优化后，整个证明过程中，并没有过于复杂的运算，这样的过程符合了重思维、轻计算的新课程改革方向. 这样的过程更是学生深度学习的过程，是对知识的内涵与本质的又一次深度学习. 这样的深度学习是高效的，在优化过程中，学生不仅仅学到了具体的结论性知识，更是学到了如何去设立目标、设而不求、构造整体思维，又如何去将定值问题进行动态处理，还培养了学生借助常规工具（向量等）求解几何问题的意识等等，这样的复习更具有对问题宏观思路的掌握，对问题本质与内涵的理解，学习的思维层次深，复习效果自然也就高效.当然点到直线公式的推导还有很多其他解法，以上是以优化运算与转变策略为例，谈谈教师如何引导学生进行深度学习，教师也可以根据具体教学需要，从其他角度进行引导深度学习. 学生的深度学习，不仅仅关乎学生的成长，也提升教师的专业素养，是教学相长的一次机会.

结束语

高三的复习不能仅仅停留在结论性知识的识记复习层面上，更应该注重对问题本质的深度复习，这样的复习才能帮助学生掌握更高层面的知识、方法、思想等，才能提升学生的核心素养，促进教师的专业素养，从而达到教学相长的目的.

参考文献：

[1]  徐树旺. 聚焦数学本质 凸显定位选择——“正弦定理（第一课时）”的教学思考[J]. 中学数学教学参考，2018（31）.

[2]  胡云飞. 基于深度学习的课堂教学思考[J]. 中国数学教育，2017（24）.