ON BOUNDEDNESS PROPERTY OF SINGULAR INTEGRAL OPERATORS ASSOCIATED TO A SCHRDINGER OPERATOR IN A GENERALIZED MORREY SPACE AND APPLICATIONS∗
Xuan Truong LE
Division of Computational Mathematics and Engineering, Institute for Computational Science,Ton Duc Thang University, Ho Chi Minh City, Vietnam Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
E-mail: lexuantruong@tdtu.edu.vn
Thanh Nhan NGUYEN
Department of Mathematics, Ho Chi Minh City University of Education,Ho Chi Minh City, Vietnam
E-mail: nhannt@hcmue.edu.vn
Ngoc Trong NGUYEN
Department of Primary Education, Ho Chi Minh City University of Education,Ho Chi Minh City, Vietnam
E-mail: trongnn@hcmue.edu.vn
Abstract In this paper, we provide the boundedness property of the Riesz transforms associated to the Schrdinger operator L= −∆ +V in a new weighted Morrey space which is the generalized version of many previous Morrey type spaces. The additional potential V considered in this paper is a non-negative function satisfying the suitable reverse Hlder’s inequality. Our results are new and general in many cases of problems. As an application of the boundedness property of these singular integral operators, we obtain some regularity results of solutions to Schrdinger equations in the new Morrey space.
Key words weighted Morrey spaces; Schdinger operator; riesz transforms; Regularity estimates
1 Introduction
In 1938, the classical Morrey space was firstly introduced by Charles B. Morrey in [23]for studying the second order elliptic equations. Several standard properties of Morrey space can be found in[1,8]and[34]. The advantage of using this functional space lies in the fact that ones can obtain better regularity properties for solutions of the boundary elliptic and parabolic equations in Morrey space. However, the regularity results for many partial differential equations can be provided as applications of the boundedness properties of several singular integral operators. By these interesting applications, many mathematicians considered the boundedness properties of singular integral operators in different kinds of functional spaces so called Morrey type spaces.
Recently, many authors have considered this kind of problem by extending to several weighted Morrey spaces, for instance [8], [16]and [13]. They have showed that the singular integral operators are not only bounded in weighted Lebesgue spaces but also in weighted Morrey spaces. In addition, lots of Morrey type spaces associated to a Schrdinger operator have been also studied (see [2, 19, 21, 27, 33]) to extend the well-known Morrey spaces. In recent years the problem related to Schrdinger operator has attracted a great deal of attention of many mathematicians; see [3–7, 9, 10, 22, 29, 35]and references therein.
Motivated by these works, we consider in this paper the boundedness property of some singular integral operators associated to a Schrdinger operator L= −∆ +V on Rn, n ≥ 3 in new generalized Morrey spaces, where the potential V belongs to RHqfor some q > n/2, i.e.,there exists a constant C =C(q,V)>0 such that the reverse Hlder’s inequality

holds for every ball B ⊂Rn. More precisely, we establish the boundedness property of the L-Riesz transform RL= D2L−1and the L-fractional Riesz transformin new Morrey type spacesrespectively. The regularity result of solutions to Schrdinger type equations in these functional spaces is also obtained as an application. We note that all notations and definitions will be introduced in the next section.
The boundedness property of the L-Riesz transform RLin Lphas been studied by Zhong[35]with a non-negative polynomial V and by Shen[29]if V ∈RHn/2. On the other hand,the boundedness of the L-fractional Riesz transforminto Lq(wq)has been proposed by Sugano[32]. With our knowledge,the boundedness property of two above operators RLandhave never been studied in our Morrey type spaceeven in the classical Morrey spaceHence, we believe that the results in this paper are general in many cases of the problem.
Moreover,we emphasize here that the spacein our paper is a generalized version of many well-known Morrey type spaces.
• In the case when V=0, w = ν =1, s= ∞ and α =0, the spacebecomes to the classical Morrey
•In 1988,Fofana[14]proposed an extension of the classical Morrey space(see[11,12])the space (Lp,Ls)θas follows

When V=0, w= ν =1 and α =0, the spacecoincides to (Lp,Ls)θ.
• In 2009, Komori and Shirai [18]introduced the Morrey type spacewith two Muckenhoupt weights w and ν as

When V = 0, s = ∞, θ = 1/q − 1/p and α = 0, two Morrey spacesare exactly the same.
• In 2009, Tang and Dong [33]defined a Morrey spaceassociated to Schrdinger operator by

When s=∞and w =ν =1, the space
• Later in 2014, Feuto [13]extended a Morrey type space (Lp(w),Ls)αequipped to the norm

It is easy to see that if V = 0, θ =and w = ν then the Morrey spacebecomes to the space (Lp(w),Ls)αin [13].
• In 2014, Liu and Wang [21]defined a weighted Morrey spaceassociated to Schrdinger operator by

When s= ∞ and ν =1, the space
The first goal of this paper is to prove the boundedness of the Riesz transform RLin the Morrey spacewhere w belongs to a class of Muckenhoupt weights Ap. We then apply this boundedness property to obtain the regularity result of solutions to Schrdinger equations(−∆+V)u=f.
Theorem 1.1Let 1 Theorem 1.2Let 1 < p < s ≤ ∞, α ∈ R, θ ∈ [0,1/p), w ∈ Ap. Assume thatLet u be a solution to the following equation then there exists a positive constant C such that In the second goal of this paper, we prove the boundedness property of the L-fractional Riesz transformin the new weighted Morrey spacewhere the weight w belongs to Ap,q. Finally, we establish the regularity of solutions to Schrdinger type equations(−∆ +V)βu=f in this space. Theorem 1.3Let α ∈ R, β ∈1 For any V ∈RHn/2, the L-fractional Riesz transformis bounded fromintoi.e., there exists a positive constant C such that Theorem 1.4Let α ∈ R,1 Assume that V ∈RHn/2andLet u be a solution to the following equation then there exists a positive constant C such that The rest of the paper is organized as follows. In the next section,we present some standard notations and definitions of Muckenhoupt weights and reverse Hlder classes. We then recall some basic and useful properties of these classes for the convenience of the reader. Moreover,a new generalized weighted Morrey space is also introduced in this section. In Section 3, we first prove the boundedness of the L-Riesz transforms RLin the weighted Morrey spaceThen we apply this boundedness property to get the regularity result for Schrdinger type equation(1.2). In the last section, we provide the boundedness of the L-fractional Riesz transformsin generalized weighted Morrey spaceFinally, we obtain the regularity result for Schrdinger type equation (1.4) by using the boundedness of the L-fractional Riesz transform We first introduce some nations that we use throughout the paper. For 1 ≤ p ≤ ∞, we denote by p′the Hlder conjugate exponent of p, i.e., Notation B(x,r) denotes a open ball in Rnwith radius r > 0 and centered at x ∈Rn.For each ball B = B(x,r) in Rnand for any λ > 0, we set λB := B(x,λr), S0(B) = B and Sj(B)=2jB2j−1B for any j ∈ N∗. We denote by Ecand χEthe complement of the set E in Rnand its characteristic function,respectively. The average integral of a function f in a measurable subset E of Rnis defined by where |E| denotes the Lebesgue measure of E. For a weight w,we mean that w is a non-negative measurable and locally integrable function on Rn. For any measurable set E ⊂Rnand the weight w, we denote In this subsection,we first recall the definitions of Muckenhoupt weights Apand the reverse Hlder classes RHq. Then we present some known properties of them which are useful for our results. Definition 2.1For 1 for all ball B in Rn. For the case p = 1, we say that w ∈A1if there exists a positive constant C such that for all balls B ⊂Rn, for a.e. x ∈B. Definition 2.2For some 1 When q =∞, we say that w ∈RH∞if there exists a constant C >0 such that for all balls B ⊂X, for almost everywhere x ∈B. For σ ≥ 1, we say that the weight w belongs to Dσif there exists a constant C > 0 such that We note that w ∈ Apimplies that w ∈ Dp. Let us introduce a positive function ρ : Rn→ R defined by: Definition 2.3We define bythe set of all functions V ∈RHn/2, such that there exists a positive constant C not depending to V such that for all x ∈Rn. Here Du and D2u denote the gradient and the Hessian matrix of a function u respectively. Remark 2.4We remark that i) if |DV(x)|≤ Cρ−3(x) then V(x)≤ Cρ−2(x) (see [17, 30]); ii) and if V(x)=|P(x)|α, where α>0 and P(x) is a polynomial, then We now recall an important property of the auxiliary function ρ(x)in the following lemma. Lemma 2.5(see [29]) Let V ∈ RHqwithThen there exists a positive constant C such that Moreover,there exists N0∈N such that for all x,y ∈Rn. Lemma 2.6Let α ∈ R, the ball B =B(y,r) in Rnand the function ρ is given by (2.2).There holds Moreover, for all m ∈ N, x ∈ B and z ∈ Sj(B), there exists N0∈ N such that for every j ∈ N and m>(N0+1)(|α|+ α). ProofIt is easy to see that if α<0 then which leads to (2.5). To estimate (2.6), we first note that by (2.3) in Lemma 2.5 for any x ∈ B,z ∈ Sj(B), we have |x − z| ∼ 2jr and ρ(x) ∼ ρ(y). Applying (2.4) in Lemma 2.5, we then get that which leads to estimate (2.6). Finally, to obtain the inequality (2.7), we first remark that for all α ∈ R. It follows that By choosing N0∈N such that we deduce estimate (2.7) from (2.8). The proof is complete. Now, we recall some basic properties of the Muckenhoupt weights and the reverse Hlder classes. Lemma 2.7(see [31, Lemma 2.1]and [15, Proposition 7.2.8]) The following properties hold: i) A1⊂ Ap⊂ Aqfor 1 ≤ p ≤ q ≤ ∞. ii) RH∞⊂ RHq⊂ RHpfor 1 iii) If w ∈ Ap,1 iv) If w ∈ RHq,1 vi) There exists δ ∈ (0,1) such that for any ball B ⊂ Rnand any measurable subset E of all B, To establish the weighted inequality for fractional integrals,we need to introduce class Ap,q. Definition 2.8We say that a weight w belongs to the class Ap,qfor 1 ≤ p < ∞ and 1 ≤ q < ∞, if there exists a positive constant C such that for any ball B in Rn We remark that if w ∈Ap,qthen for any ball B in Rn. The connection of Ap,qand Amis also showed in the following lemma. Lemma 2.9(see [18, Remark 2.11])The following statements are true: i) For any p>1, if w ∈ Ap,qthen wq∈ Aq, and w−p′∈ Ap′. ii) w ∈ A1,qif and only if wq∈ A1. Let us now introduce a new Morrey type space which is a generalized version of many well-known Morrey type spaces. Defniition 2.10Let α ∈ R, θ ∈ [0,1),We denotethe space of all measurable functionssuch that where the function ρ is defined by(2.2). In the case of w ≡ ν,we denotefor the simplicity. In [29], Shen proved that the operator RLis a Caldern-Zygmund operator if V is a non negative polynomial and RLis bounded in Lpif V ∈RHn/2. In this paper, we obtain the general result in the new Morrey spaceunder the assumptionLet us introduce a kernel K(x,y) associated to operator RLas follows We next state several lemmas which are useful to prove our main result about the boundedness property of the L-Riesz transform RLin Morrey spaceThe proof of Lemma 3.1 can be found in [26, Lemma 3.6]. Lemma 3.1Let V ∈For any k >0 there exists a positive constant C such that Lemma 3.2Let w ∈ Ap, 1 ≤ p< ∞ and f ∈ Lp(w). Then holds for every ball B ⊂Rn. ProofWe consider two cases p=1 and p>1. For the first case p=1, since w ∈A1we obtain that for every ball B ⊂ Rn. For the second case p> 1, by Hlder’s inequality and the definition of Ap, one has for every ball B ⊂Rn. The proof is complete. Lemma 3.3Let 1 ≤ p < s ≤ ∞, α ∈ R, θ ∈ [0,1/p) and w ∈ Ap. For any ball B =B(y,r) and m>0 let us set Then there exists a constant C > 0 not depending on B such that for alland m>(N0+1)(|α|+ α), there holds ProofBe the definition of the function F in (3.2), we can estimate Using the inequality (2.7) in Lemma 2.6, we obtain from (3.4) that Thanks to (2.9) in Lemma 2.7 and remark that 1/p − θ ≥ 0 in the above inequality, we can estimate A as follows which leads to (3.3) with noting that 1/p − θ ≥ 0. The proof is complete. Proof of Theorem 1.1Let f ∈and the ball B = B(y,r). We decompose f by Thanks to Lemma 3.1 and the inequality (2.6) in Lemma 2.6, for all m ∈N, one has Applying Lemma 3.2, we obtain from (3.5) that which leads to for almost everywhere x ∈B. From (3.6) and the boundedness of the Riesz transform RLin the weighted Lebesgue space Lp(w), we get that Multiplying two sides of (3.7) byone has Applying (2.5) in Lemma 2.6, we can estimate J1as where we use the doubling property (2.1) of w in the last inequality. Combining this estimate and inequality (3.3) in Lemma 3.3, there exists a positive constant C such that Finally, by the definition ofwe can conclude that which finishes the proof. Proof of Theorem 1.2The boundedness property of D2u can be obtained by the boundedness of RLf in Theorem 1.1. To consider L-fractional Riesz transformwe recall the classical Riesz potential. In 1974, Muckenhoupt and Wheeden [24]proposed the boundedness property for the classical Riesz potential Iβdefined by in weighted Lebesgue space Lp(w). Their result is stated in the next lemma. Lemma 4.1Let 0 < β < n, 1 < pand w ∈ Ap,q. Then the Riesz potential Iβis bounded from Lp(wp) into Lq(wq), i.e., there exists a positive constant C such that for all f ∈Lp(wp). We denote by Kβ(x,y) the kernel associated to the L-Riesz potentialAn estimate of the kernel Kβ(x,y) is directly obtained by using estimation (11) in [20, page 241]. Proposition 4.2Letm ∈ N, m ≥ 2. There exists Cm>0 such that for any ball B, for all x ∈ B, y ∈ (2B)cthere holds where β1=2β − 1. Combining the definition of the Riesz potential Iβin(4.1), Lemma 4.1 and Proposition 4.2 we may obtain the next lemma. Lemma 4.3Let α ∈ R,1 For any w ∈Ap,q, the L-fractional Riesz transformis bounded from Lp(wp) into Lq(wq),i.e., there exists a positive constant C such that for all f ∈Lp(wp). We now proof the following lemma. Lemma 4.4Let α ∈ R,1 For any ball B = B(y,r) and m > (N0+1)(|α|+ α), there exists C > 0 not depending on B such that for althere holds where the function W(f,B) is defined by ProofBy (2.7) in Lemma 2.6, we can estimate Thanks to estimate (2.9) and noting that 1/q − θ ≥ 0, one deduces from (4.4) that Taking the supremum both sides of (4.5), by the definitions ofwe obtain that Since 1/q − θ >0 there holds which completes the proof. Proof of Theorem 1.3Let B = B(y,r) be a ball in RnandWe decompose f as follows We can estimate J1by the boundedness from Lp(wq) into Lp(wp) ofin Lemma 4.1, we have where the last inequality is obtained by inequality(2.5)in Lemma 2.6. From(4.6),the doubling property of wqgives us Thanks to Proposition 4.2, for every m ∈ N, m ≥ 2, there exists Cm> 0 such that for all x ∈ B, z ∈ (2B)cthere holds where β1= 2β − 1. For x ∈ B and z ∈ Sj(B), we see that |x − z| ∼ 2jr. Combining (4.8)and (2.6) in Lemma 2.6, one obtains for all m ∈ N, m ≥ 2. Using Hlder’s inequality and assumption Ap,qof w it follows that One implies from (3.5) and (4.10) that which guarantees the estimate of J2as follows The proof is complete by combining this inequality to Lemma 4.4, estimate (4.7) and the definition of Proof of Theorem 1.4The boundedness property of Du can be obtained by the boundedness ofin Theorem 1.3.







2 Preliminaries
2.1 Notations


2.2 Muckenhoupt weights and reverse Hlder classes









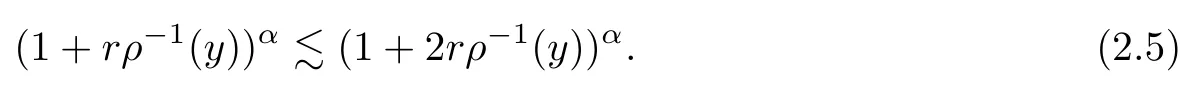






0 such that w ∈ RHq+ǫ.




2.3 A generalized Morrey type space

3 Boundedness of L-Riesz Transform



















4 Boundedness of L-fractional Riesz Transform










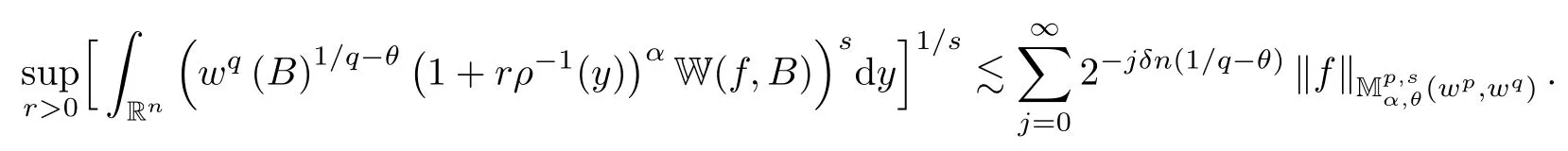










 Acta Mathematica Scientia(English Series)2020年5期
Acta Mathematica Scientia(English Series)2020年5期
