二维声全息的δ函数约束型射线波叠加法
张阳 向宇 石梓玉


摘 要:利用波叠加法进行声场重建是一个病态逆问题,极小的测量噪声就可能导致重建结果完全失真.传统方法是在重建过程中结合正则化手段以提高稳定性,但当系统矩阵由于全息模型配置不当而严重病态时,即便采用正则化手段也难以获得令人满意的结果.利用强指向性的狄拉克δ函数对二维Helmholtz方程的解集进行形状约束,使得约束后的解集成为具有δ函数指向特性的射线波函数.利用该射线波函数替换传统波函数后可使系统矩阵趋于主对角占优的良态形式,从而提高重构稳定性.通过数值仿真验证了该射线波函数在二维声场重建中的正确性及稳定性,同时给出了射线波函数叠加项数的一种选择方法.结果表明:利用该射线波函数不仅可以有效地计算二维声全息问题,而且降低了系统矩阵的条件数,提高了声场重建稳定性.
关键词:波叠加法;近场声全息;狄拉克δ函数;重建稳定性
中图分类号:TB52 DOI:10.16375/j.cnki.cn45-1395/t.2020.04.003
0 引言
近场声全息技术[1](Near-field acoustic holography,NAH)是一种噪声源识别、定位及声场可视化的强有力工具.近几十年来,众多学者通过对近场声全息进行深入研究后相继提出了空间Fourier变换算法[2-3] (Spatial fourier transform,SFT)、边界元算法[4-5](Boundary element method,BEM)、波叠加法[6](Wave superposition method,WSM)等全息算法,均取得了较好的效果.但是,这些方法也存在着相应的不足,例如:空间Fourier变换算法要求声源面与全息采样面必须具有规则的形状,且在利用快速傅里叶变换算法(Fast fourier transform,FFT)进行重建计算时无法避免窗效应与卷绕误差[7-8];边界元法虽适用于任意形状的声源面及全息面,但在计算时存在复杂的奇异积分处理及特征波数处解的非唯一性问题[9],严重影响了计算精度和效率.波叠加法由于将源强点布置在声源面内部的一个虚拟边界上,因此,不会出现边界元法中的奇异积分处理,但仍存在着不足——即特征波数处声场解的非唯一性及重建病态问题.针对非唯一性问题,国内外学者已经进行了大量研究,并相继提出了复数形式的Burton-Miller型组合层势法[10]、复数矢径波叠加法[11]、附加源波叠加法[12]等,均取得了很好的效果.而对于重建病态问题,目前的方法一般是在求解过程中应用正则化以得到稳定的近似解[13-15].但常规的正则化方法仅是通过数学手段对病态方程组进行后期的数值处理,并没有改善物理模型本身的不适定性,因此,若当模型配置不当而导致问题本身严重病态时,即使再结合正则化也难以得到令人满意的近似解.针对该问题,参考文献[16]从改善波叠加法物理模型本身的不适定性出发,提出了一种无需正则化就能稳定重建声场的射线等效源法[16],为改善基于波叠加法的声场重构病态问题拓展了一条全新的思路.该射线等效源法是利用格林函数的各阶导数替换传统波叠加法积分核函数,以使积分方程在离散后得到的系统矩阵呈现主对角占优的良态形式,从而改善重构病态问题.但是格林函数在求导阶数较高的情况下表达式将变得非常复杂,难以计算,且在二维情况下,格林函数的导数并不具备单一方向的指向性,因此,需另寻一种构造射线波函数的方法.
本文利用强指向性的狄拉克δ函数对二维Helmholtz方程的解集进行形状约束,使得约束后的解集成为具有δ函数指向特性的射线波函数.由于无需对格林函数求导,因此,极大地提高了计算效率和稳定性.文中给出了该射线波函数的详细推导过程和叠加项数的选择方法,并利用二维脉动圆环和随机点声源对本文方法的正确性及稳定性进行了验证.
1 基于波疊加法的声场重建算法[6]
波叠加的基本思想为:振动体向外辐射的声场可由置于其内部的所有虚拟等效源所产生的声场叠加代替,而这些虚拟等效源强度可通过匹配声源面或全息面的相关信息得到.如图1所示,考虑一任意形状的二维振动体,其中[S]为振动体边界,[E+]为振动体外部辐射域.假设在振动体内部的虚拟边界[SE]上布置等效源,则外域[E+]中任意场点[r]处声压可表示为:
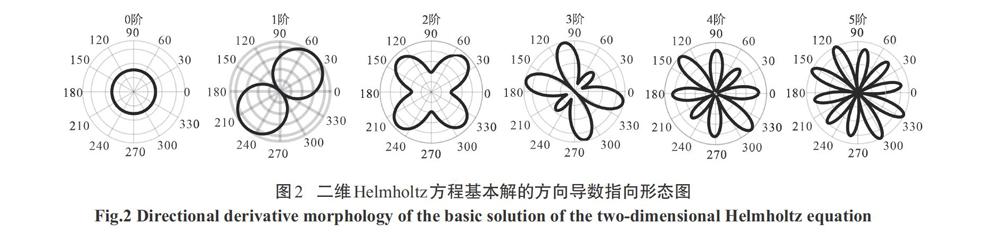
以上就是基于波叠加法的声场重建算法.由于系统矩阵[GHE]通常是病态矩阵,因此,利用式(6)求解源强是一个病态逆问题.文献[16]中对系统矩阵的病态性进行详细分析后指出:由于传统波叠加法采用的是球面形式的格林函数作为波函数,因此,将会导致系统矩阵由于列线性相关性过强而病态.为解决该问题,文献[16]通过对三维Helmholtz方程的基本解(即自由场格林函数)求方向导数的方式构造了一种具有强指向性的射线波函数.利用该射线波函数替换传统波叠加法的球面波函数后改善了系统矩阵的病态性,提高了重建稳定性.但在二维情况下,Helmholtz方程基本解的方向导数并不具备三维情况下的单一方向指向性,而是呈发散状,如图2所示,图中求导方向为[1, 1].因此,需另行探索一种可适用于二维平面的射线波函数构造方法.
2 δ函数约束型射线波函数的构造
显然,式(8)的解可作为波叠加法波函数,且通过匹配不同的展开项系数[An],可使其具有任意形状的波函数.换言之,若能够匹配出适当的展开项系数[An],就可以使式(8)成为具有单一方向指向性的射线波函数.本文的方法是利用具有指向性的狄拉克δ函数作为约束函数对式(8)进行形状约束,由此匹配出相应的系数[An],使得约束后的式(8)具备与辅助函数相同的指向性质.
狄拉克函数[δx-x0]是一个具有脉冲性质的广义函数,它在[x=x0]点处具有无穷集中的指向性,而该指向性可以由其逼近序列[δnx-x0]体现,如图3所示,图中给出了狄拉克[δx-x0]函数的其中一个逼近序列:[πn11+n2(x-x0)2].
可以看到,随着[n]的增大,逼近序列[δnx-x0]在[x=x0]点处越来越“尖”,即指向性越来越强,符合射线波函数的指向性要求.因此,可以考虑将[δx-x0]作为约束函数对式(8)进行形状约束.
如图4所示,假设第[i]个等效源点[rEi]与其对应主测点[rHi]的位置已确定,以该等效源的位置为原点设置一个与绝对坐标系平行的局部坐标系[(xi, yi)],此时该等效源点[rEi]与其对应主测点[rHi]之间的距离为[rHi, Ei=rHi-rEi],主测点[rHi]与局部坐标[xi]轴的夹角为[φxi, Hi].显然,若该等效源[rEi]所辐射的是射线波,那么该射线波的主指向与局部坐标[xi]轴的夹角也必然是[φxi, Hi].假设使用δ函数对该波函数进行约束,那么该δ函数的形式为[δφ-φxi, Hi].这里[φ∈0, 2π],表示将δ函数在该等效源(局部坐标原点)处沿周向展开,且在主指向角[φxi, Hi]处具有脉冲指向性.
假设δ函数[δφ]在图4的局部坐标系[(xi, yi)]下可由式(8)的无穷叠加项展开,那么有:
由于波函数的指向特性只与角度有关,因此,在式(9)中已将式(8)中的变量[r]写为常量[rHi, Ei],表示在以等效源点[rEi]为原点,[rHi, Ei]为半径的圆上计算声压幅值;[Ani]表示局部坐标系[(xi, yi)]下的展开项系数.值得注意的是,由于δ函数是没有具体数学表达式的广义函数,因此,式(9)表示当展开项系数为[Ani]时,式(9)右边的无穷项叠加将成为与δ函数一样的脉冲指向函数.由此容易推知,若取有限叠加项,式(9)的右边就成为δ函数的一个逼近序列,并且该逼近序列满足Helmholtz方程.
由图5可以看到,随着叠加项数[m]的增大,波函数在主指向角方向的指向性越来越强.若采用上述射线波函数替换传统波叠加法中的球面波函数[Gr, rEi],各等效源点所辐射的声场如图6所示.
由图6可以看到,此时各等效源所辐射的声场在其对应主测点处最大,而在其他非主测点处迅速衰减.因此,等效源与全息面间系统矩阵的主对角元素将比非主对角线元素大得多,系统矩阵呈现主对角占优的形式.等效源点与全息采样点之间的系统矩阵[KHE]为(为便于计算,不妨令等效源点与全息采样点数目一致):
[KHE=KrH1, E1, φx1, H1, φx1, H1, rH1, E1KrH1, E2, φx2, H1, φx2, H2, rH2, E2…KrH1, EN, φxN, H1, φxN, HN, rHN, ENKrH2, E1, φx1, H2, φx1, H1, rH1, E1KrH2, E2, φx2, H2, φx2, H2, rH2, E2…KrH2, EN, φxN, H2, φxN, HN, rHN, EN??KrHN, E1, φx1, HN, φx1, H1, rH1, E1KrHN, E2, φx2, HN, φx2, H2, rH2, E2…KrHN, EN, φxN, HN, φxN, HN, rHN, EN]
其中:系统矩阵[KHE]的第[i]行、第[j]列的元素为:
[KHEij=KrHi, Ej, φxj, Hi, φxj, Hj, rHj, Ej=2π2πn=-m+mH2nkrHi, EjH2nkrHj, Ejein(φxj, Hi-φxj, Hj)],[rHi, Ej=rHi-rEj],[rHj, Ej=rHj-rEj],[φxj, Hi]表示[rHi]与局部坐标[(xj, yj)]横轴[xj]的夹角,[φxj, Hj]表示等效源[rEj]对应的主指向角,各变量见图6.同理可得等效源与任意场点间的系统矩阵[KRE].
当利用系统矩阵[KHE]和[KRE]进行声场重建时,式(5)—式(7)可写为:
[PH=KHEQHE] (15)
[QHE=K+HEPH] (16)
[P=KREK+HEPH] (17)
式(15)—式(17)即為基于本文提出的射线波函数的声场重建公式.
3 数值算例仿真与讨论
3.1 二维脉动圆环声场重建验证
利用二维脉动圆环作为声源验证运用本文方法进行声场重建的正确性.已知半径为[rS],周边产生均匀径向振速幅值为[v0]的脉动圆环在距离圆心[r]处所辐射声压的解析解为[20]:
为验证本文方法在声场重建计算中的正确性,在不添加噪声的情况下进行声场计算.选取射线波函数的叠加项数[m]分别为2、4、5、8、10、15,其余参数设置如下:声源面半径[rS=]1 m,等效源面半径 [rE=]0.2 m,全息采样面半径[rH=]1.1 m.采用不同叠加项数计算得脉动圆环表面声压如图7所示.
由图7可以看到,利用本文方法计算所得的表面声压无论是實部还是虚部都能与解析声压相吻合,说明本文方法能够正确地反演声场.
为进一步探究声场重建效果与叠加项数之间的关系,取叠加项数[m=0?30],频率[f=350 Hz],并在不加噪声与加噪声([SNR=30 dB])的两种情况下分别进行计算.为更加直观地体现系统矩阵性态对于重建稳定性的影响,本文所有数值仿真均不使用任何正则化手段,直接使用Matlab中的“inv”函数对矩阵求逆.定义声压相对误差[δsp]:
将叠加项数[m]的取值区间分为0~3、4~26、27~30三种情况分别讨论图8的结果.
1)当叠加项数为0~3时,无噪声情况下的声压重建误差均在[5%]以内,说明此时能够正确地进行声场重建计算.但在加噪声的情况下,并不能很好地重建声场.这是因为此时的射线波函数指向性不足、系统矩阵的病态性并未得到足够的改善,放大了测量噪声.
2)当叠加项数[m=4~26]时,无噪声情况下的重建误差都小于[5%],加噪声情况下的重建误差也都控制在5%~10%之间.这说明在此区间内,原本病态的系统矩阵得到了改善,因此能够稳定地进行声场重建.
3)当叠加项数m=27~30时,随着叠加项数的增大,其声压误差也随之变大.这是由于过大的叠加项数导致射线波函数的指向性过强,进而各虚拟等效源所辐射的能量在其主指向处过于集中,而在非主指向处衰减过快,由此导致了部分系统信息的缺失,因而无法很好地重建声场.同时也发现,加噪声与不加噪声的两条误差曲线在27项后几乎重合,这说明此时虽然已经不能很好地重建声场,但噪声并未对重建结果产生明显影响.这意味着此时系统矩阵的病态性已经得到了改善,有效地抑制了噪声对于重建结果的干扰.
由以上分析可知,射线波函数的叠加项数[m]须在合理的范围内进行选择.
3.2 辅助面法
可采用辅助面法[21]确定叠加项数[m].辅助面法的基本思想是:在全息采样面与声源面之间选取一辅助面[Γ],通过比较辅助面上测量声压与重建声压相对误差的最小值来确定合适的叠加项数.该问题可描述为:
3.3 随机点声源声场重建验证
由于实际结构声源并无解析解可循,所以难以进行声场重建验证.但由惠更斯叠加原理可知,任意声源皆可看作无数点源的集合.因此,可用随机布置的一系列不同强度的点声源考察本文方法在实际复杂声场重建中的正确性及稳定性.
已知数量为[n]的点源在二维平面所辐射的声场为:
式中:[σi]为第[i]个点源的强度系数;[gr, ri]为二维Green函数.在仿真计算中,取点源数量 [n=30],并随机分布于中心位于坐标原点、半径为[1]的圆域内,点源强度随机从[0?1]中选取.
该算例参数如下:节点数[N=70],频率 [f=]800 Hz,信噪比[SNR=40 dB],等效源半径[rE=]0.4 m,全息面半径[rH=]1.1 m.辅助测量面为半径[rΓ=]1.05 m的圆环.其中,叠加项数取值范围[m=0?25],重建观测点数量为[50],均匀分布在[-2, 1]到[2, 1]的线段上.
首先利用辅助面法计算不同叠加项数下的声压误差,如图9所示.由图9可以看到,辅助面上的声压相对误差在叠加项数[m=6~20]时大致相同,因此,为了提高计算效率,选取叠加项数[m=6].利用选出的叠加项数进行声场重建计算,结果如图10所示.可以看到,在传统方法已无法得到稳定重建结果的情况下,本文方法仍可得到令人满意的稳定计算结果.表1给出了传递矩阵[ΚHE]的条件数,可以看到,本文方法有效地降低了系统矩阵的条件数,明显改善了系统矩阵的病态性.
4 结论
基于将传统球面波函数替换为强指向性射线波函数以改善系统矩阵病态性的思想,提出了一种构造射线波函数的新方法.该方法利用狄拉克δ函数对二维Helmholtz方程的解集进行形状约束,得到了一系列具有δ函数指向特性的射线波函数.通过数值仿真验证了该射线波函数在二维声场重建中的正确性及稳定性,同时给出了射线波函数叠加项数的一种选择方法.计算结果表明:本文方法不仅可以有效地计算二维声全息问题,而且降低了系统矩阵的条件数,提高了声场重建的稳定性.本文虽仅对二维情况进行了推导与探究,但其基本理论和方法可以方便地推广到三维情况,因此,仍具有一定的研究价值.
参考文献
[1] WILLIAMS G E,MAYNARD J D. Holographic imaging without the wavelength resolution limit[J]. Physical Review Letters,1980,45(7):554-557.
[2] WILLIAMS E G,MAYNARD J D,SKUDRZYK E. Sound source reconstructions using a microphone array[J].Journal of the Acoustical Society of America,1980,68(1):340-344.
[3] VERONESI W A,MAYNARD J D. Nearfield acoustic holography (NAH)-II-holographic reconstruction algorithms and computer implementation[J].Journal of the Acoustical Society of America,1987,81(5): 1307-1322.
[4] MAYNARD J D,WILLIAMS E G,LEE Y. Nearfield acoustic holography:I. Theory of generalized holography and the development of NAH[J].Journal of the Acoustical Society of America,1985,78(4): 1395-1413.
[5] CUNEFARE K A,KOOPMANN G H,BROD K. A boundary element method for acoustic radiation valid for all wavenumbers[J].Journal of the Acoustical Society of America,1989,85(1):39-48.
[6] KOOPMANN G H,SONG L M,FAHNLINE J B. A method for computing acoustic fields based on the principle of wave superposition[J].Journal of the Acoustical Society of America,1989,86(6):2433-2438.
[7] FLEISCHER H,AXELRAD V. Restoring an acoustic source from pressure data using wiener filtering[J]. Acta Acustica United with Acustica,1986,60(2):172-175.
[8] KWON H S,KIM Y H. Minimization of bias error due to windows in planar acoustic holography using a minimum error window[J].Journal of the Acoustical Society of America,1995,98(4):2104-2111.
[9] CHAPPELL D J,HARRIS P J. A Burton–Miller inverse boundary element method for near-field acoustic holography[J].Journal of the Acoustical Society of America,2009,126(1):149-157.
[10] BENTHIEN W,SCHENCK A. Nonexistance and nonuniquness problems associated with integral equation methods in acoustics[J]. Computers and Structures,1997,65(3):295-305.
[11] 向宇,黄玉盈. 基于复数矢径的波叠加法解声辐射问题[J].固体力学学报,2004,25(1):35-41.
[12] 夏雪宝,向阳. 基于附加源波叠加法的声辐射计算研究[J].振动与冲击,2015,34(1):104-109,144.
[13] TIKHONOV A N,ARSENIN Y V. Methods for solving ill-posed problems[M].Moscow:Nauka,1979.
[14] WILLIAMS E G. Regularization methods for near-field acoustical holography[J].Journal of the Acoustical Society of America,2001,110(4):1976-1988.
[15] CHARDON G,DAUDET L,PEILLOT A,et al. Nearfield acoustic holography using sparsity and compressive sampling principles[J].Journal of the Acoustical Society of America,2012,132(3): 1521-1534.
[16] 石梓玉,向宇,陆静,等. 一种提高声场重构稳定性的射线等效源法[J].广西科技大学学报,2019,30(3):1-7,21.
[17] 陈心昭,毕传兴.近场声全息技术及其应用[M].北京:科学出版社,2013.
[18] 许伯熹. Helmholtz方程解的唯一延拓及逆源问题[D].上海:復旦大学,2014.
[19] JEFFREYS H,JEFFREYS B. Methods of mathematical physics[M]. 3rd. Cambridge:Cambridge University Press,1999.
[20] WU W T,OCHMANN M. Boundary element acoustics fundamentals and computer codes[J].Journal of the Acoustical Society of America,2002,111(4):1507-1508.
[21] 毕传兴.基于分布源边界点法的近场声全息理论与实验研究[D].合肥:合肥工业大学,2004.

