基于机器学习的脉动源格林函数预报初探
常宏宇,朱仁传,黄 山
(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室,上海 200240)
格林函数法是计算波浪与结构物相互作用问题的一个重要方法,快速准确地计算格林函数及其偏导数是准确获得浮体作用力的关键和难点。三维势流水动力理论中格林函数法分为简单格林函数法和自由面格林函数法(亦称为复杂格林函数法)。数值计算时前者需要的离散自由面,流场截断,远场辐射边界的处理都是需要克服的难点。后者则特指采用无限流域中满足线性自由面条件的波动格林函数,数值实现时,不需要离散自由面,网格量少,其困难在于复杂的格林函数本身的计算[1]。为此以无因次表达的脉动源格林函数为例,进行机器学习研究,以期获得高效高精度的计算方法。
精度和效率是格林函数法有效实施的两个基本要素。频域零航速自由面格林函数,按照表达形式的不同,可分为Havelock型、Haskind-Havelock型以及Kim型格林函数,其数值计算有偏微分方程法、数值积分法、级数展开法以及多项式逼近法。解析逼近计算高效但有时难以控制精度,为了避免精度损失往往需要对区域进行有效划分。Noblesse[2-3]采用指数积分形式提出了两种互补的近场和远场单积分表示法,用渐近展开级数和收敛升序级数分别计算源点和场点之间不同距离的格林函数,当无量纲坐标趋近零时,给出了两个互补的泰勒级数展开式。Telste和Noblesse[4]基于文献[3]的工作,将计算域划分为5个子域,发表了一个数值计算代码来评估格林函数及偏导数。Newman[5]将速度势表示为Bessel函数、Struve函数与一个有限积分之和,使用龙贝格积分求解得到双精度的格林函数值。之后他还提出了一种将解析展开式和切比雪夫多项式逼近结合的可达10-6精度的级数展开法[6]和一种全域切比雪夫多项式逼近法[7],其中文献[6]中的级数展开方法是商业软件WAMIT的计算核心基础。Chen[8-9]等提出了一种基于多项式级数逼近的算法,采用双重切比雪夫逼近和特殊函数法对无限水深和有限水深下的格林函数进行计算,算法应用在水动力计算软件HYDROSTAR中[10]。Clement[11]基于格林函数的二阶微分方程提出了一种完全不同的方法,其难点在于初始化。近年来,Shen等[12]提出了一种二阶常微分方程算法,算法达到10-6精度,相比级数展开法更高效。Duan等[13]和Shan等[14]分别给出了一种基于全域划分的级数展开法,全域可以达到10-9精度。Wu等[15]提出了一种全域多项式拟合方法,将格林函数及其梯度表示为基本空间奇点、非振荡的近场项和波动项,针对近场项给出简单的近似计算式,只涉及实变量和基本初等函数(代数、指数、对数),方法可达10-3精度,且极大地提高了计算效率。Shan等[16]基于Newman[7]的工作,优化了剩余函数的选择区域,对子域重新划分,改进了切比雪夫逼近法。
机器学习是人工智能的核心,包括许多可以通过经验和数据来自动改进的计算机算法,如支持向量机和神经网络等。当前机器学习在海洋工程领域上也有所应用:董宝玉[17]研究了一种基于遗传算法优化支持向量机多分类的方法,扩展到高维空间应用于船舶柴油机故障诊断中,成功对故障模型进行预判;迟岑[18]利用支持向量机进行无人艇自主避障中静止障碍物的聚类,利用ELAMN预测模型中动态障碍物的运动状态,顺利完成避障。深度学习是机器学习的第二次浪潮,Hinton等[19]曾指出,多隐层神经网络具有优异的特征学习能力,其实质是通过构建多隐层的神经元模型,使用海量训练数据来学习有代表性的特征,最终提升分类或预测的准确性。
前人对复杂格林函数的计算多是数值积分或以解析函数为主的多项式逼近,前者精度高但计算耗时,后者计算高效但精度难以控制。三维频域深水绕辐射问题的脉动点源格林函数的数值计算分析研究较多,有直接积分计算、多项式逼近等,为便于研究和比较,以脉动点源格林函数为例,先参考Newman方法[5],使用龙贝格积分得到高精度的格林函数数据库。引入机器学习方法,采用深度学习函数库Keras对数据库进行学习,通过反向传播算法迭代更新模型参数,并调节模型深度和激活函数等超参数,建立格林函数的神经网络预报模型。分别对全局和局部的预报精度和效率进行研究,并与相应的数值积分和多项式逼近方法[15]比较,验证了该方法的可行性和高效性。研究表明,基于神经网络的格林函数高精度预报模型,能够保证较高的精度和效率,为水动力问题求解和数值计算难题提供了新的思路。
1 脉动点源格林函数解及其无因次表达
无限水深频域脉动点源格林函数多见于教材,见文献[20]。若场点P坐标为(x,y,z),源点Q坐标为(ξ,η,ζ),波数k0=ω2/g,脉动点源格林函数的表达式为:

(1)

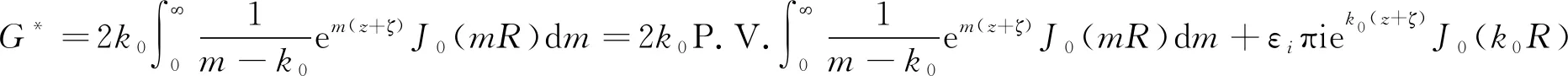
(2)
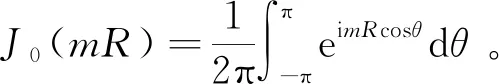
将式(2)中的广义波数m对k0做无因次化处理,得G*关于变量θ的单重积分表达式为:
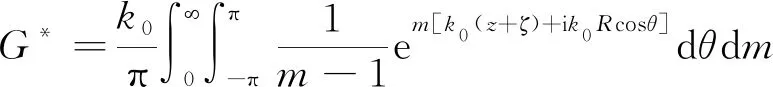
(3)
记Z=z+ζ,X=k0R,Y=-k0Z=-k0(z+ζ),α=-Y+iXcosθ。由于(z+ζ)≤0,故X≥0,Y≥0,交换积分次序,格林函数归纳为:

(4)
进一步可将格林函数表示成下面的θ型单重积分形式:

(5)
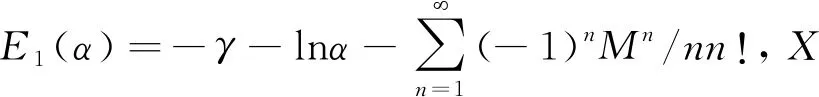
同时将式(2)按照Newman的方法[5],将波动部分G*表达为以下无因次化形式:

(6)
其中,Y0是第二类贝塞尔函数,H0是Struve函数。采用龙贝格积分计算式(6),得到10-15精度的格林函数G*的数据库。
2 机器学习方法介绍
使用神经网络算法对模型进行学习。神经网络是一种经典的机器学习算法,其中的误差逆传播(BP)神经网络是一种监督式学习算法,具有很强的非线性映射能力。Hornik[21]证明,只需一个包含足够多神经元的隐层,多层前馈网络就能以任意精度逼近任意复杂度的连续函数。神经网络中最基本的成分是神经元模型,如图1所示。
在每一层的连接中,输入层向量用x表示,经激活函数f处理,输出为f(W1x-θ),激活函数需使用非线性函数,如sigmoid、tanh、relu等。给定训练数据,神经网络的所有参数即各层之间的连接权重ωi与偏置项θ,其求解是一个最优化问题。

损失函数求解的优化问题中,常沿着梯度方向不断下降来找到极小值。常用的梯度下降法有批梯度下降、随机梯度下降以及小批量梯度下降法。训练过程中一个epoch表示使用训练集中的全部样本训练一次,batchsize表示批大小,即每次训练使用的训练集样本个数。梯度下降法在梯度平缓的维度下降非常缓慢,在梯度陡峭的维度易抖动,陷入局部极小值或鞍点。而且选取合适的学习率比较困难,只有在原问题是凸问题的情况下,才能保证以任意精度取得最优解。非凸情况下,需要对梯度下降进行优化,比如Momentum,Adagrad,Adam等算法,可以避免陷入极大值极小值,设置得当可以得到全局最优解。为了防止模型过拟合,文中还将探索正则化和随机失活的影响。
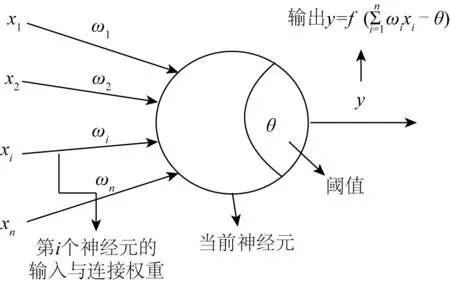
图1 神经元模型Fig. 1 Neuron model
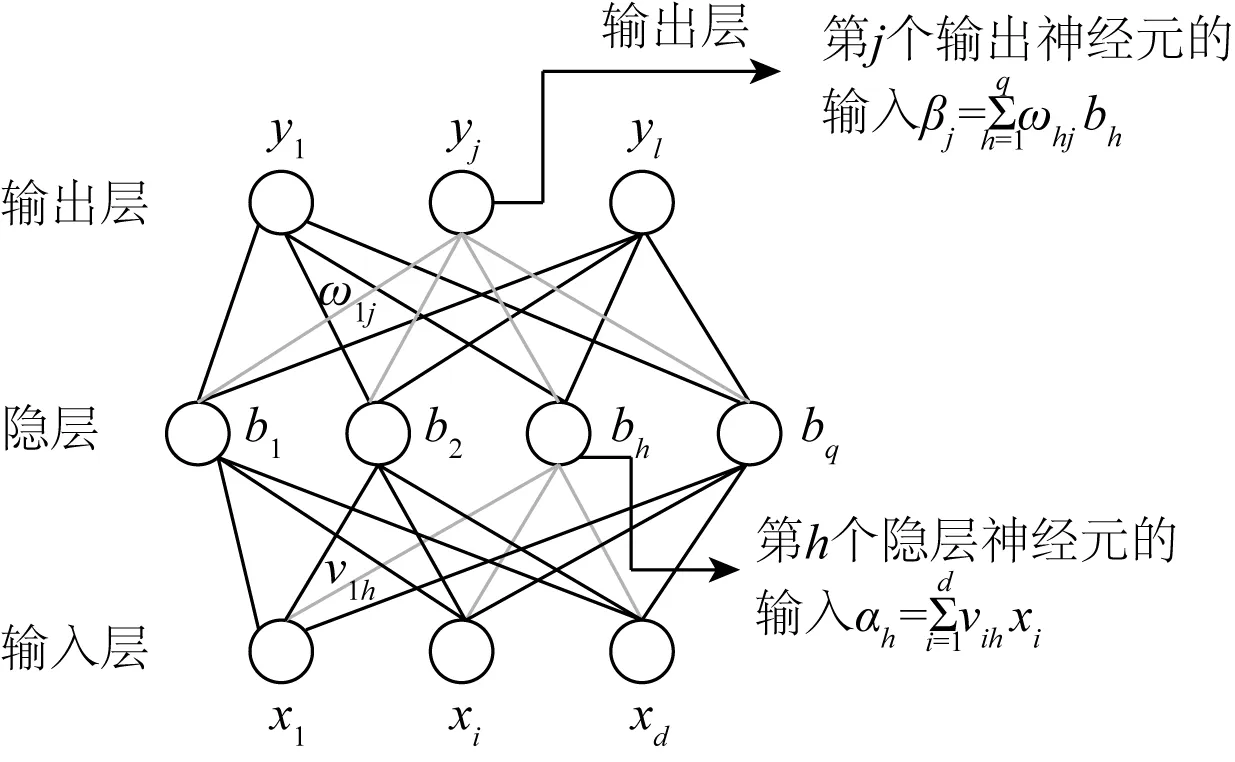
图2 神经网络中的变量符号Fig. 2 Variable symbols in neural networks
Keras由python编写,作为Tensorflow和Theano等的高阶应用程序接口,可以方便地进行深度学习模型的调试、评估、应用和可视化。关于格林函数的预报,可以直接使用Keras训练好的h5格式模型文件,也可以导出模型权重等参数后重构模型以便灵活计算。
3 格林函数的预报验证
3.1 格林函数数据库样本密度
使用龙贝格积分计算式(6)得到高精度的无因次格林函数数据库。格林函数数值计算部分结果如表1所示。计算结果与文献[5]结果完全一致,且应用于求解无航速S175实船的水动力系数和运动响应的结果与WAMIT一致,表明了该格林函数数值计算结果的准确性。

表1 数值计算结果Tab. 1 Numerical results
由于格林函数对任何频率通用,应用时只需生成关于无因次水平距离X和水深Y的统一数据库。考虑船长、船宽和吃水,结合性能评估的无因次频率范围发现,X不小于20,Y不小于8时即可基本满足浮体的性能评估要求。首先探究数据库采样的密度,X范围为0~20,Y范围为0~8,分别设置采样密度为0.05×0.01、0.05×0.05和0.10×0.10的数据为训练集,采样密度为0.01×0.01的数据作为验证集,进行精度分析。全局训练设置两个隐层,各128个隐层节点,不加正则化和随机失活。模型参数设置如表2所示。

表2 网络结构Tab. 2 Network structure
预报结果的误差分析(对误差绝对值取负对数)如图3所示。预报数据的误差分布统计如图4所示。误差分布统计图中,横轴负对数坐标误差为5时,表示预报误差在10-4~10-5之间。如图4所示,模型1预报数据的误差分布更加均匀,平均误差更小,预报误差有99.81%在10-3至10-6之间,预报误差小于10-4的比例为66.21%,明显高于模型2的9.34%和模型3的32.76%。3种训练集取样密度均可保证10-4以上的平均误差。将全局训练时格林函数数据库的取样密度设置为0.05×0.01,分区域训练时的取样密度可以适当加大,得到原始的无因次格林函数数据库如图5所示。
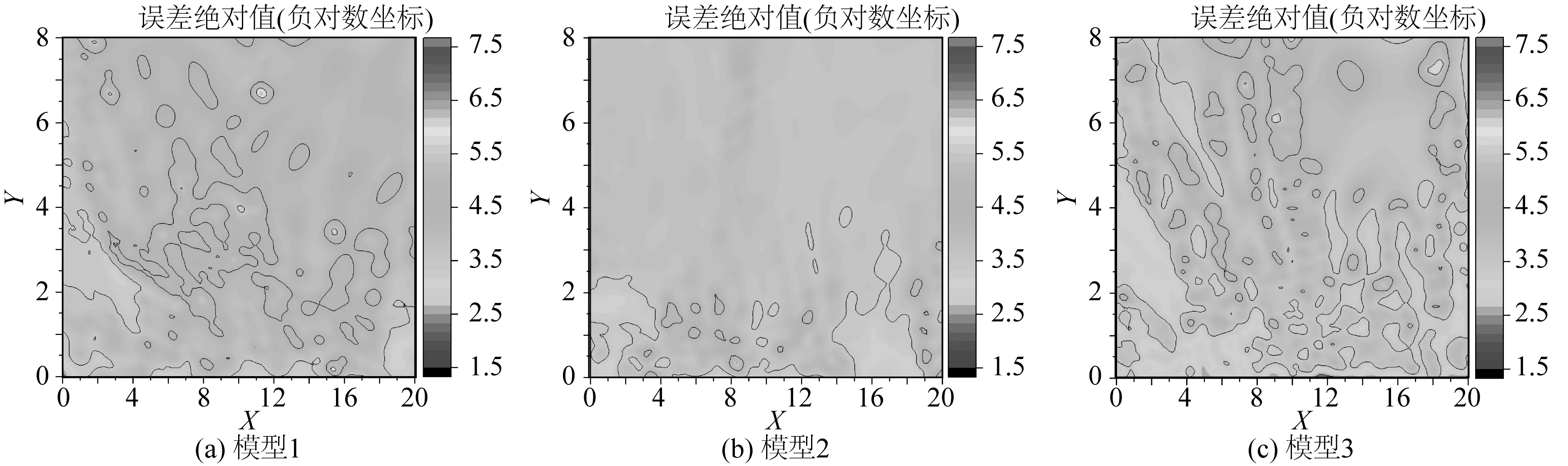
图3 不同训练样本密度下误差分布Fig. 3 Error distribution for different training sample densities
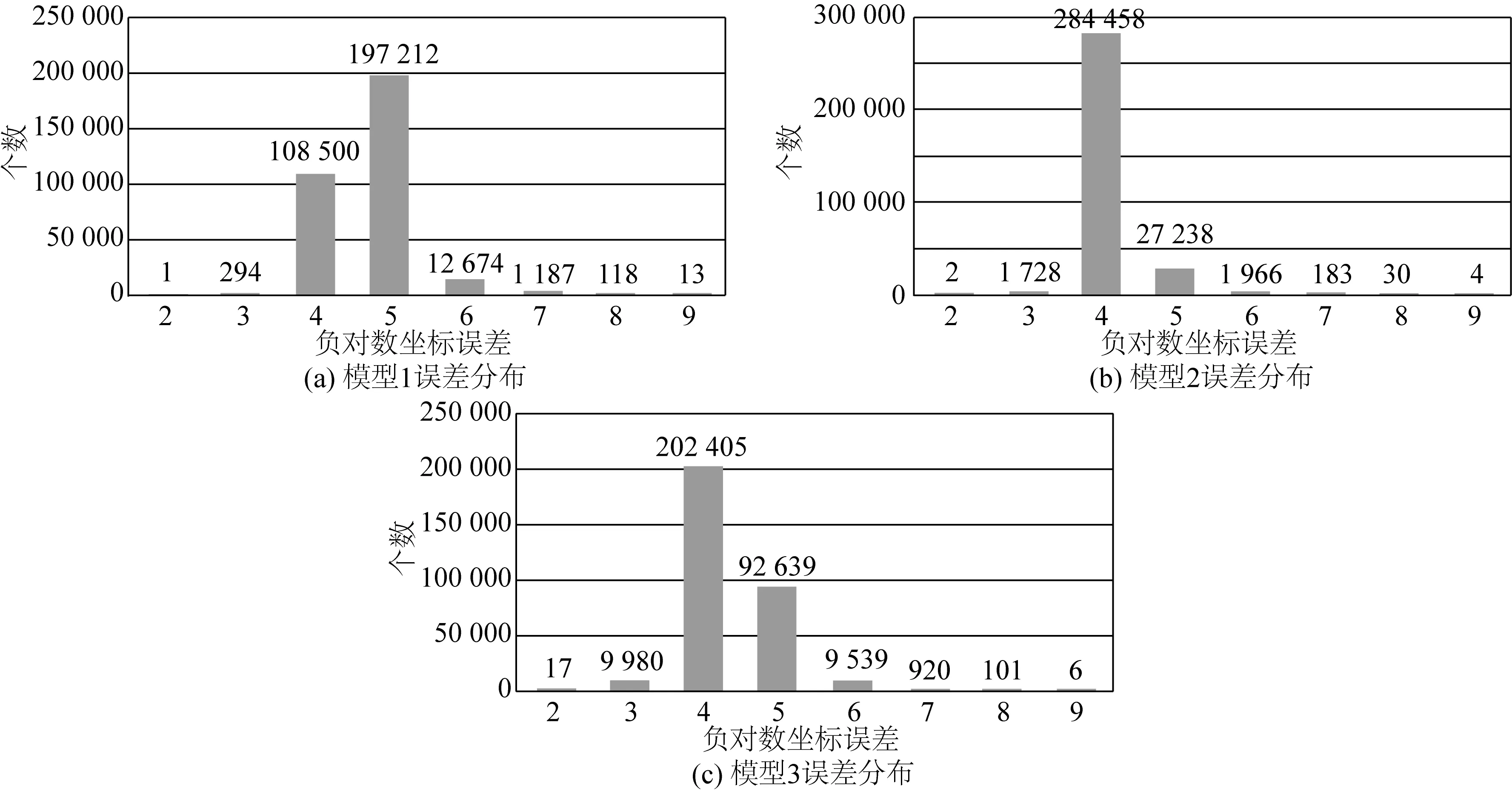
图4 误差分布统计Fig. 4 Statistics of error distribution

图5 全局格林函数库Fig. 5 Global Green function library
3.2 全局训练优化和精度分析
定义全连接神经网络结构,利用3.1节的格林函数数据库,在Keras下进行学习,考虑正则化、随机失活及Adam等优化算法。训练过程显示,模型在10 000个epoch后收敛速度减缓,根据调参结果,设置如表3所示的8种网络结构。训练后导出模型,使用X范围为0~20,Y范围为0~8,间隔均为0.01的密集样本点作为测试集,对预报精度进行分析。

表3 全局训练网络结构Tab. 3 Network structure for global training
模型5和7中加入正则化以及Dropout后,模型的训练和测试误差明显偏大,表明在密集训练数据下,不需要考虑过拟合。其余各模型预报的格林函数结果如图6所示。
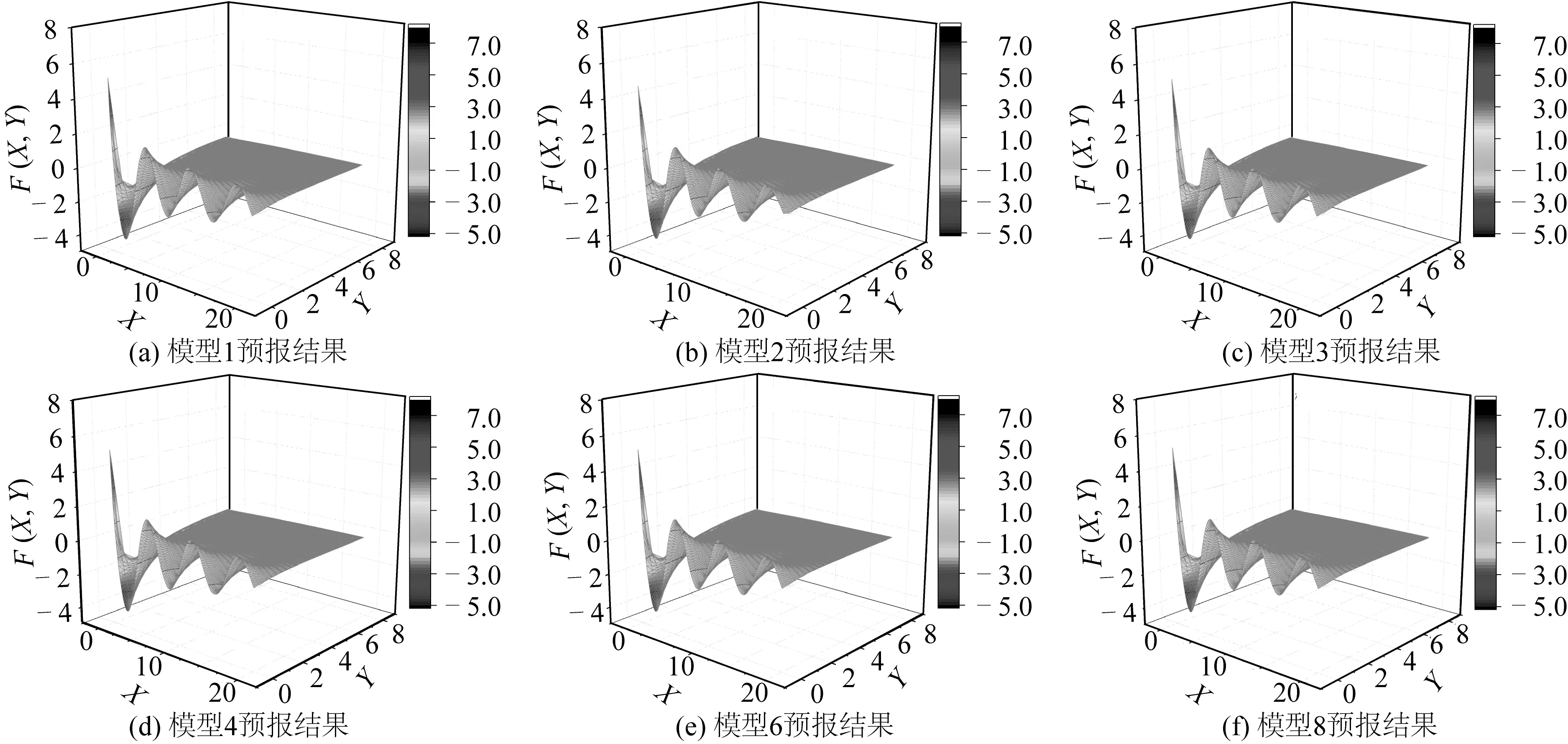
图6 全局预报结果Fig. 6 Global forecast result
预报结果的误差分析(误差绝对值取负对数)如图7所示。由图7可知在区域边缘附近,误差扰动往往比较大,实际应用过程中这一区域要做特殊处理。结果表明sigmoid激活函数和Adam优化算法可以加快模型训练速度和预报精度。其他条件一定时,增加神经网络模型深度会增加训练时间,但拟合精度大致不变。模型1预报误差有99.81%在10-4至10-6之间,预报误差小于10-5的比例为66.21%,这个精度可以满足水动力计算需求。模型1部分预报结果展示如表4所示。

图7 全局预报误差分布Fig. 7 Error distribution for global forecast

表4 预报结果展示Tab. 4 Presentation of forecast results
3.3 分区训练优化和精度分析
如图6所示,Y接近0时原始格林函数图形波动较大。图7表明这一区域的误差较其他区域也偏大。为提高预报精度,考虑分区学习,将全局划分为4区域:区域1中,X取0~3,Y取0~3;区域2中,X取3~20,Y取3~8;区域3中,X取0~3,Y取3~8;区域4中X取3~20,Y取0~3。4个区域分别进行模型学习。
使用的分区训练数据完全互补,但并不重合,在预报时,区域交界点只属于4个分区中的某一个区域。各区域的原始格林函数图像与图5一致。
3.3.1 区域1精度分析
区域1上,X和Y每隔0.01取样,共90 000个训练数据。设置表5所示的4种网络结构。

表5 区域1网络结构Tab. 5 Network structure for zone 1
结果表明,模型2和4加入正则化后,预报误差明显增大,说明在训练样本密集的情况下,模型不会过拟合,后续将不再考虑正则化。模型1和3预报结果的误差分析(误差绝对值取负对数)如图8所示。

图8 区域1误差分布Fig. 8 Error distribution of zone 1
平均误差最小的模型1预报误差有99.51%在10-3至10-6之间,误差小于10-4的比例为94.56%。
3.3.2 区域2精度分析
在区域2上,X每隔0.02,Y每隔0.01取样,共426 351个训练数据。本节及之后的分区训练都设置如表6所示的4种网络结构。

表6 区域2/3/4网络结构Tab. 6 Network structure for zones 2/3/4
预报结果的误差分析(误差绝对值取负对数)如图9所示。

图9 区域2误差分布Fig. 9 Error distribution of zone 2
平均误差最小的模型1的预报误差有96.53%在10-4至10-7之间,预报误差小于10-5的比例为96.55%。
3.3.3 区域3精度分析
在区域3上,X和Y均每隔0.01取样,共150 300个训练数据。预报结果的误差分析(误差绝对值取对数)如图10所示。

图10 区域3误差分布Fig. 10 Error distribution of zone 3
平均误差最小的模型2的预报误差有97.17%在10-4至10-7之间,预报误差小于10-5的比例为99.80%。
3.3.4 区域4精度分析
在区域4上,X和Y每隔0.01取样,共510 000个训练数据。预报结果的误差分析(误差绝对值取对数)如图11所示。

图11 区域4误差分布Fig. 11 Error distribution of zone 4
平均误差最小的模型2的预报误差有96.86%在10-4至10-7之间,预报误差小于10-5的比例为21.94%。
结果表明,分区预报时,各区域的精度指标基本都优于全局预报,绝大部分区域的精度可达10-4以上。文献[22]的研究表明对于水动力计算这个精度基本满足。
分区训练时,分区训练数据完全互补,但是并不重合。在预报时,区域交界点只属于4个分区中的一个区域,在后续的水动力系数和运动响应的计算中,替代的子程序只调用4个分区代码中的某一个即可。
3.4 预报效率对比
为了评估机器学习方法的效率,将神经网络模型与数值积分方法及多项式逼近方法进行效率对比,对比的数值积分方法有Newman方法[5]和θ型单重积分,多项式逼近方法为文献[15]的全局逼近。
单次计算平均用时,指在不同的预报数据的规模下,全部完成预报的用时与数据规模的比值,表示多次计算的平均用时。python中的矩阵计算依赖于numpy函数库,对向量和矩阵的计算进行了优化加速。神经网络模型在进行较大规模数据的预报时,进行前馈网络的逐层计算,等价于多个矩阵计算。算法在预报时将全部输入视为大规模矩阵进行加速,在数据规模更大时,神经网络算法会表现出更好的性能,单次计算的平均用时更短。而这也是机器学习算法的优势,数据库以及训练算法一旦形成,可以广泛应用于不同对象,而不需要每次都重新计算。预报效率的对比如表7所示。

表7 不同数据规模下单次计算平均用时 Tab. 7 Average time of single calculation for different data sizes (μs)
如表7所示,机器学习预报的计算效率低于以解析函数为主的多项式逼近,高于θ型单重积分数值方法,稍低于Newman的龙贝格积分数值方法。
4 结 语
采用深度学习函数库Keras,对脉动点源格林函数数据库进行学习,建立了神经网络预报模型,并展开了模型预报精度和效率的分析研究。得到如下结论:
1) 机器学习格林函数库建立的神经网络模型预报格林函数是可行的。机器学习模型预报的格林函数在99%以上的区域可以保证10-4及以上的精度,能够达到实用精度的要求。
2) 全局拟合中,区域边缘处的预报误差偏大。论文采用的分区训练思路,有效地提高了精度。在分区拟合中,区域边缘处的误差会大于区域内部,后续可考虑扩展训练区域来提高精度。
3) 机器学习模型预报的效率优于直接数值积分计算,低于以解析函数为主的多项式逼近,稍低于Newman的龙贝格积分数值方法。
以上工作主要为建立在非常成熟的脉动点源格林函数研究基础上的机器学习初步探索研究,此格林函数的计算有Newman的龙贝格数值积分方法和相关的解析逼近方法。机器学习建立的预报模型在此格林函数的计算效率上并没有优势,但比直接求解数值计算的效率高很多。由此可以想象,对于那些复杂格林函数,特别是不能用解析多项式逼近表达的,如有航速三维频域辐射格林函数,以及难以计算且效率低下的复杂函数等,可以合理地应用机器学习方法,进行建模替代计算。本方法为提高水动力问题求解效率,解决传统计算难题提供了新的思路。

