一类稳态Poisson-Nernst-Planck方程的L2投影的超收敛

覃柳术， 阳 莺,2， 唐 鸣

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.桂林电子科技大学 广西高校数据分析与计算重点实验室，广西 桂林 541004)

Poisson-Nernst-Planck(PNP)被广泛应用于生物分子[1]、电化学[2]和半导体[3]等领域中。它是由描述浓度梯度和电场下离子通量的Nernst-Plancks(NP)方程和描述电势的Poisson方程耦合而成。

由于PNP方程是一类耦合的非线性非对称的偏微分方程，极少情况下能够找到解析解，通常使用数值方法寻找其近似解。常用的数值方法包括有限差分法、有限体积法、有限元法。有限元法可以很好地处理不规则区域，且其解的收敛速度取决于解的正则性。由于NP方程存在电势梯度这一低阶量，使得有限元解近似的电势梯度精度较低，方程存在收敛速度慢甚至发散的问题。为了提高有限元解的导数的精度，超收敛方法被提出。

L2投影是实现超收敛的重要方法之一。文献[5]给出了一致网格上三角线性元和二次元在整体区域上L2投影的超收敛理论结果。文献[6]给出了任意四边形网格剖分下Poisson方程的L2投影超收敛方法，并给出了超收敛的结果。文献[7]提出了一种基于L2投影的梯度恢复技术，证明了它具有高阶的超收敛性，并将该方法用于斯托克斯方程和弹性方程的求解。文献[8]将L2投影用于求解Poisson-Boltzmann方程，达到了超收敛的效果。

鉴于此，针对一类PNP方程，引入L2投影算子，给出了一致网格和非一致网格的误差分析，同时通过数值实验进行验证。

1 预备知识

设Ω是R3中的有界区域，且满足Lipchitz连续，∂Ω为其边界。使用标准的Sobolev空间记号Wm,p(Ω)和相应的范数和半范数，当p=2时，记

Ws,2(Ω)=Hs(Ω)，‖·‖s,p,Ω=‖·‖Ws,p(Ω)，

其中v|∂Ω=0是在迹的意义下定义的，(·,·)表示L2内积。

考虑如下稳态PNP方程：

(1)

其中：pi为第i种离子的浓度；qi为第i种离子的电荷量；φ为静电势；ε为介电常数。方程(1)的边界条件考虑齐次的Dirichlet边界条件p1=p2=φ=0。

方程(1)的弱形式为：

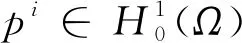
(pi,v)+(qipiφ,v)=(Fi,v),

(2)

(3)

线性有限元空间定义为

Sh={v∈H1(Ω):v|∂Ω=0且

v|e∈p1(e),∀e∈Γh(Ω)},

其中p1(e)表示线性多项式集合。

假设方程(1)存在唯一解(φ,pi)，i=1,2，式(2)、(3)的有限元离散格式为：

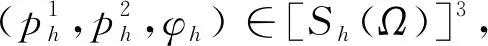
(4)

(5)

2 超收敛的误差分析

L2投影算子[5]Qh:L2(Ω)→Sh(Ω)满足正交关系：

(w-Qhw,v)=0, ∀v∈Sh(Ω)。

(6)

其中：C为与h无关的正常数；θ=min(s,1/2)。

证明由式(2)～(5)和Poincare不等式易证引理1成立。

引理2剖分的网格为一致剖分，有下列不等式成立[9-10]：

‖w-Qhw‖0,Ω≤Ch1+t‖w‖1+t,∀w∈H1+t(Ω),

(7)

∀v∈Sh(Ω),

(8)

其中η∈(W1,∞(Ω))3。

‖εφ-Qh(εφI)‖0,Ω≤Ch1+t,

(9)

其中0≤t≤1。

证明由式(7)得

‖εφ-Qh(εφI)‖0,Ω≤

‖εφ-Qh(εφ)‖0,Ω+

‖Qh(εφ)-Qh(εφI)‖0,Ω≤

Ch1+t+‖Qh(εφ-εφI)‖0,Ω。

(10)

对∀η∈(W1,∞(Ω))3，根据式(8)可得

(Qh(εφ-εφI),η)=(φ-φI,εQhη)=

-(-φ-φI,div(εQhη))≤Ch1+t‖η‖0,Ω。

(11)

联合式(10)、(11)可推出式(9)成立。

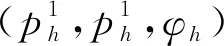
‖εφ-Qh(εφh)‖0,Ω≤

(12)

其中0≤t≤1。

证明由式(9)得

‖εφ-Qh(εφh)‖0,Ω≤

‖εφ-Qh(εφI)‖0,Ω+

‖Qh(εφI)-Qh(εφh)‖0,Ω≤

Ch1+t+‖Qh(εφI-εφh)‖0,Ω。

(13)

根据引理1，对任意的φ∈(L2(Ω))3，可得

(Qh(εφI-εφh),φ)=

(14)

由式(13)、(14)可推出式(12)成立。

以上结论均建立在均匀网格上，以下将在非均匀网格上对L2投影算子进行误差分析。

在非均匀网格上定义L2投影算子Qh:L2(Ω)→SH(Ω):

(w-Qhw,v)=0,∀v∈SH(Ω)。

(15)

定义投影算子：

引理3[10]若

且h≪1，则

(16)

其中0≤t≤1。

定理3若

则

‖εφ-Qh(εφh)‖0,Ω≤

(17)

证明由式(15)得

‖εφ-Qh(εφh)‖0,Ω≤

‖εφ-Qh(εφ)‖0,Ω+

‖Qh(εφ-εφh)‖0,Ω≤

CH1+t+‖Qh(εφ-εφh)‖0,Ω,

其中0≤t≤1。对于任意的ψ∈(L2(Ω))d，有

(Qh(εφ-εφh),ψ)=

由引理3可得

|(Qh(εφ-εφh),ψ)|≤

也即

‖Qh(εφ-εφh)‖0,Ω≤

文献[4]的数值实验表明，

从而有

3 数值实验

用数值实验验证L2投影算子构造的超收敛格式的有效性。在Fortan4.0环境下编译，所用计算机配置为Inter(R)Core(TM) i5-6500 CPU@2.50 GHz，内存4 GiB。构造如下带有L2投影算子的Gummel迭代算法。

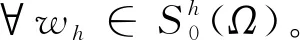
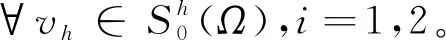
4)当

成立时，停止迭代；否则，令m=m+1，返回步骤2)。

考虑一类带真解的方程(1)，求解区域Ω=[0,1]3，q1=1,q2=2，右端函数Fi和边界条件依赖于解析解。解析解定义为：

用线性元对方程(1)进行离散，用算法1进行求解，得到有限元解梯度和Qh(φh)逼近真解梯度的L2误差估计曲线如图1所示。图1中‖φ-φh‖0,Ω表示电势真解梯度和有限元解梯度的L2模误差；‖φ-Qh(φh)‖0,Ω表示电势真解和用L2投影算子构造Qh(φh)的L2模误差。从图1可看出，用L2投影算子构造Qh(φh)逼近真解的梯度优于有限元解的梯度。

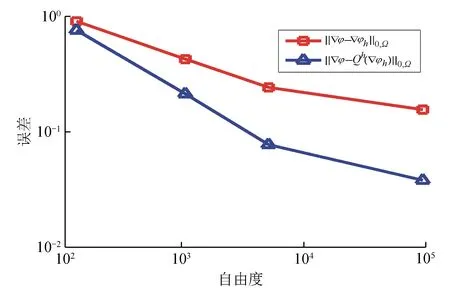
图1 有限元解梯度和Qh(φh)逼近真解梯度的L2误差估计曲线

4 结束语

通过引入L2投影算子，对PNP方程进行了误差分析，对一类带真解的稳态PNP方程进行了数值实验。实验结果表明，相比于有限元解的梯度，利用L2投影算子构造的Qh(φh)逼近真解的梯度的精度更高。