从希尔伯特的第13问题谈起1)

林永静

(温州职业技术学院建筑工程系，浙江温州325035)

1900年，德国数学家希尔伯特在第二届世界数学家大会上提出了著名的23个问题，这23个问题是数学家的梦想，许多数学家用一生试图攻克其中的一个或几个问题。这些问题，一些已经得到圆满解决，一些得到部分解决，也有一些尚未解决。为了解决希尔伯特问题，数学家发展出很多新的数学分支，可以说希尔伯特问题引领着20世纪现代数学发展的主流，很少有科学问题在科学发展历史上起着如此重要的作用。

本文介绍的是希尔伯特第13问(一般七次代数方程以二变量连续函数之组合求解的不可能性)：七次方程x7+ax3+bx2+cx+1=0的根依赖于3个参数a，b，c，x=x(a，b，c)，这个三元函数可否用二元函数表示出来？同理，图1所示的三维物体上的应力是一个三元函数，可否用二元函数表示出来？

1 第13问的发展历史

在希尔伯特第13问提出之后，俄罗斯数学家柯尔莫果洛夫(Andrey Nikolaevich Kolmogorov)作出了重要贡献，部分证明了该问题：任意一个多元函数可以用有限个三元函数表达出来。1957年，他的弟子、数学家阿诺尔德(Arnold)在连续函数的情形下证明了该问题：在连续函数的情形下，任意一个多元函数可以用有限个二元函数表达出来。1964年，维土斯金(Vituskin)推广到连续可微情形。该问题对解析函数情形则未解决。

严格的数学表述[1-2]是：定义在n(n≥2)维立方域[0，1]n上任意一个连续n元函数f(x1，x2，···，xn)，可以用连续的一元函数φpq和gq表示为

令人遗憾的是，所有的数学证明都是存在性的证明，而不是构造性的证明。以式(1)为例，虽然式(1)显示了多元函数可以用一元函数的复合来表示，但由于函数的复合在数学上过于复杂，一元函数φpq和gq实际上是无法求得的。长期以来，沿着多元函数用一元函数来表示的思路，一直没有具体的实现方法。

但是，如果将第13问在工程意义上放低要求，在工程概念上理解为：一个多元函数的工程需要的有效数据，用低维函数表达出来，或者是一个多元函数用低维函数最优地表达出来。这样一来，多元函数的一元函数表示的空间就比较大了，有可能具体地构造出来。

2003年，我国科学家宋健在第13问的工程表示上取得了进展，将多元函数在低维可视空间里构造性地表达出来。其研究是在高维空间中寻求由一元函数组合成的最佳基，使给定的高维函数展成项数最少和收敛最快的级数。

2 工程问题

(1)力学计算中的高维数烦恼。在力学问题中，当采用有限元求解三维弹性体问题，网格加密时计算量会迅速增加，计算量非常大甚至无法求解，这个问题称为高维数烦恼。作者发现，在塑性极限分析和岩土工程的计算中，也有高维数烦恼。

(2)有限元线法。和其他有限元方法不同，有限元线法的函数构造形式采用了一元函数，二维问题里一个方向上是解析的线，另一个方向上是离散的。有限元线法的计算效率比较高，性质也比较好。有限元线法可认为来源于第13问。

(3)控制论问题。在控制论中，低维可视空间中表达高维数据或函数已成为科学研究、系统模拟和工程设计的基础工作。寻求用数量最少的单变量函数组合表达高维函数，在控制论中可能有广泛应用。

(4)流形学习，全称流形学习方法。流形学习是信息科学领域的研究热点。在理论和应用上，流形学习方法都具有重要的研究意义。假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。

(5)PGD(proper generalized decomposition)。PGD是一种有效的多维逼近方法。PGD方法采用变量的分离表示形式逼近响应面，该形式可以有效减少展开项数目。由于其展开项数目随阶数线性增长，该方法为多不确定系统的分析提供了可能。

这些工程问题比较多，这里不一一介绍。以下重点介绍作者的研究工作：高维数烦恼的延拓Kantorovich法解决方案。

3 高维数烦恼

高维数问题随着精度要求的提高，计算量会迅速地增加，因此计算量往往非常庞大。例如对于三维问题，网格加密会遇到三维烦恼[3-4]。

盈亏平衡分析法又称保本分析法或本量利分析法，是利用数学化的会计分析模型和图文来揭示、分析固定成本、变动成本、服务量、利润等变量之间的关系，为财务预测或决策提供财务信息咨询的一种分析方法［2］。其计算公式为：

当用有限元求解时，最后归结为求解一个含P个未知数的线性方程组AU=F。当网格很细密时，这是一个大型方程组。我们知道，大型有限元问题中主要的计算量与存储耗费在解这个方程组上。对n=1，2维情形，求解这个方程组并不是很困难。但对三维问题就不容易了。下面以三维泊松方程为例说明。

设Ω是立方体，作均匀剖分，每个维度用N个节点，总节点为N3，每个节点上一个未知数，共有未知数P=N3。若用直接法求解线性方程组，P阶方阵A的半带宽约为B≈N2，应存储的系数总数K=BP=N5。分解A为三角阵时所需的乘除运算次数M≈B2P/2=0.5N7。在每秒能完成百万次乘除运算的计算机上将耗时t=M/106。表1列出了N=10，20，40，80方案的规模。

表1 三维Poisson方程的有限元计算规模

4 第13问的启发

由于第13问的证明是存在性的，不是构造性的，长期以来，沿着多元函数用一元函数来表示的思路，一直没有具体的实现方法。但是已有的数学成果提供了重要的启发：沿着这条思路，可能有利于实现更高效的近似表示。更浅白地说，与全离散法等其他方法相比，用一元函数来表示多元函数可能是更节省的“捷径”，可以用尽可能少的数据量包含尽可能多的信息量。从物理上看，相当于能量或信息高度集中在几条主要的谱线上，而不是均匀平坦地分布。这意味着在足够高的工程精度内，一个多元函数近似等价为有限个一元函数的表达式，使问题因维数降低而大大简化。因此，这种高效的近似表示具有重要而广泛的应用价值。简单地以数据存储为例，n元函数在计算机上存储，数据量为O(Nn)，其中N为每个维度的节点数。如果n元函数用一元函数来近似表示，则存储数据量为O(N)，是原来的1/Nn-1倍，这样的数据压缩效率是非常高的，尤其当n较大的时候。

由于多元函数用一元函数来表示的研究方向存在着相当大的困难，特别是数学分析上非常困难，因此，目前的两项研究前沿采用一元函数的乘积和来近似表示多元函数。

第一项研究是延拓Kantorovich法，主要通过数值试验加上定性分析进行研究。三维延拓Kantorovich法采用张量积形式的函数逼近形式，代入三维泊松方程的能量泛函，经整理并取变分后，可以导出一套耦合的积分微分方程组。其中一个方向的一元函数较多为优势方向，算法的迭代过程将不再按各个维度轮换求解的迭代，而是围绕着这个优势方向旋转迭代。

另一项研究是控制论专家宋健的论文《高维函数和流形在低维可视空间中的最优表达》[5]，主要从数学分析方面进行研究。这是他经过数年的研究积累得到的突破性成果，得到了数学家丘成桐等的高度评价。他在平方可积函数空间中寻求用数量最少的一元函数组合表达多元函数，得到梯度算子非线性积分方程组。证明了该方程组的本征元列构成规范正交系，任何平方可积的多元函数均可按此正交系展成长度最短和收敛最快的级数。

5 张量积形式的三维延拓Kantorovich法的解决方案

当采用简单的试函数逼近形式，即u(x，y，z)=时，迭代过程不收敛。经过对各种试函数逼近形式的尝试，文献[6]发现如下特定的张量积的函数逼近形式可以解决该数值困难

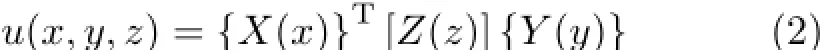
其中，{X(x)}={X1，X2，···，Xn}T，{Y(x)}={Y1，Y2，···，Yn}T，n为叠加项的项数，[Z(z)]是n×n的矩阵，即[Z(z)]i，j=Zij，i=1，2，···，n，j=1，2，···，n。

下面以立方体域上的三维Poisson方程的Dirichlet问题为例，具体阐述三维延拓Kantorovich法的算法实施过程。三维泊松方程对应的能量泛函为其中Ω为立方体域[-a，a]×[-b，b]×[-c，c]。

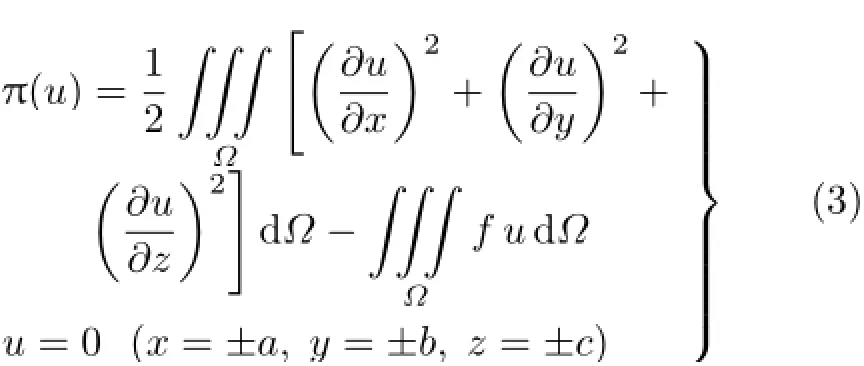
将式(2)的试函数逼近形式代入式(3)，经整理并取变分后，可以导出如下一套耦合的积分微分方程组

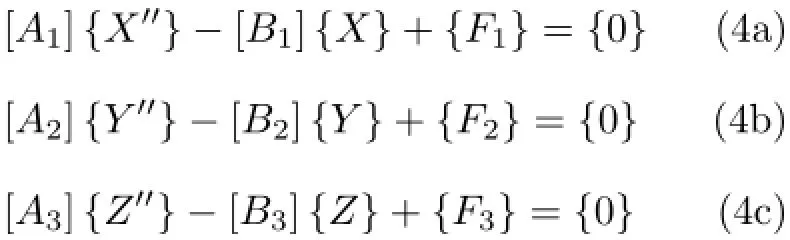
边界条件为

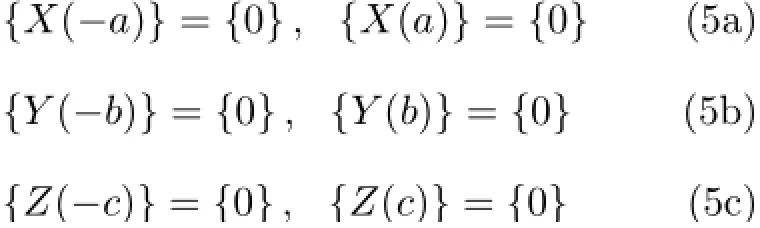
算例三维泊松方程的Dirichlet问题

立方体域上的该方程见图2。设定边界条件为

给定数据为a=b=c=1，f=2。

图2 三维泊松方程

取初始试函数为

表2 给出了取不同项数时的计算结果，如中心点位移u0，面中点导数∂u/(∂z)，∂u/(∂x)。参考解为级数解N=100的结果。

表2 取不同项数的中心点位移和面中点导数(循环轮数=5)

6 结论

希尔伯特第13问启发了用一元函数表示多元函数的思路。延拓Kantorovich法沿着这条思路，对解决高维数烦恼进行了探索，并取得了一定的进展。数值结果表明，延拓Kantorovich法是用一元函数逼近多元函数的一种有效途径，不失为高维数烦恼的一种有发展潜力的解决方案。

希尔伯特问题的意义不仅在于重要数学问题的解决，而且在于求解问题的过程中会生长出新的数学、好的数学，所以人们评价希尔伯特问题是“会下金蛋的鹅”。作者认为，之所以希尔伯特问题富有生机活力、善于生长出新的数学，是因为希尔伯特问题找到了数学的重要源头。德国《自然》杂志发表过这样的观点：现在世界上很难有一位数学家的工作不是以某种途径导源于希尔伯特的工作。

希尔伯特第13问的多元函数的低维表示是众多领域的普遍性问题，这些领域的研究者和爱好者，在闲暇时间里，何不漫步到问题的源头，从希尔伯特第13问这里得到一些启发呢？