具有连续分布时滞的切换分布参数系统反馈控制

鲍乐平,李腾辉

(1.太原工业学院自动化系,太原 030008；2.太原科技大学电子信息工程学院,太原 030024)

切换系统是混杂系统的一种重要类型。它包括一组子系统和描述子系统之间如何切换的切换规则,整个切换系统受控于切换规则[1]。由于在工程实践中的应用,如机器人控制[2]、电力系统控制[3]等,切换系统在近二十多年得到了广泛的研究[4-7]。

按照建模方法的不同,切换系统分为集中参数切换系统和分布参数切换系统(或者称切换分布参数系统)。有关切换分布参数系统的研究一直是国际控制理论研究领域的难点。近十年来,切换分布参数切换系统受到了广泛关注[8-12]。此外,时滞广泛存在于工业系统中,是系统产生不稳定的一个重要因素。近些年来,有关时滞系统的研究有大量的报道[13-19]。

文献[13]研究了时滞切换系统的稳定性问题,但考虑的切换系统不是分布参数系统；文献[12]研究了切换分布参数系统的H控制问题,但没有考虑具有分布时滞的情形。文献[14-15]利用线性矩阵不等式(linear matrix inequality，LMI)方法研究了时滞分布参数系统稳定性和镇定性问题；文献[16]利用LMI方法研究时滞分布参数系统的H控制问题；文献[17]对具有分布时滞的不确定中立型分布参数系统研究了滑模控制,设计了滑模控制器；文献[18]对具有变时滞和连续分布时滞的分布参数系统进行了研究,设计了使得闭环系统稳定的状态反馈控制器，但没有考虑切换。从已有的相关文献来看,对于具有连续分布时滞的切换分布参数系统控制问题研究还未见报道。

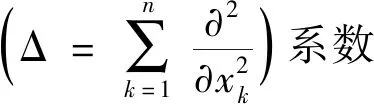
1 问题描述

考虑具有连续分布时滞的切换分布参数系统为

Ad1iW(x,t-γ1)+

(1)

其状态反馈控制为

U(x,t)=KiW(x,t)

(2)

由式(1)、式(2)得到闭环系统为

Ad1iW(x,t-γ1)+

(3)

式中：i∈Θ={1,2,…,N},表示该切换系统具有N个子系统；(x,t)∈Ω×(0,+),x表示坐标,t表示时间,表示具有光滑边界∂Ω的有界区域Ω=Ω1∪Ω2∪…∪ΩN,Ωi∩Ωj=∅(i,j∈Θ)；W(x,t)∈Rn表示系统的状态向量；U(x,t)∈Rs表示控制；为Laplace算子；Di为耗散系数,Di>0(∀i∈Θ);Di、Ai、Bi、Ad1i,Ad2i(∀i∈Θ)为具有适当维数的已知矩阵；Ki为待定矩阵；时滞γ1>0,γ2>0为已知常数,记h=max{γ1,γ2}。

系统边值条件为

W(x,t)=φ(x,t),(x,t)∈Ω[-h,0]

(4)

W(x,t)=0,(x,t)∈∂Ω[-h,0]

(5)

(6)

式中：φ(x,t)为光滑函数；n为边界∂Ω上的单位外法向量。

研究的目的是设计状态反馈控制器[式(2)]和切换规则,使得闭环切换分布参数系统[式(3)]渐近稳定。

引理Jensen不等式[19]：已知向量函数ω(·):[a,b]→Rn,a0,有

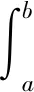
2 主要结果

定理已知具有连续分布时滞的切换分布参数系统[式(1)],其初边值条件为式(4)、式(5)。如果对于任意给定的矩阵Q1i、Q2i>0,存在矩阵Pi>0,Ki,使以下矩阵不等式成立:

(7)

(8)

切换规则：

(9)

证明构造切换Lyapunov-Krasovskii函数为

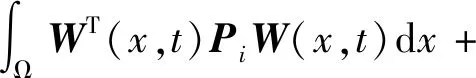
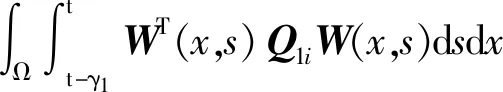
(10)

因为Pi、Di为正定矩阵,则PiDi为正定矩阵。类似文献[12]推导,根据高斯收敛定理、Poincare不等式以及边界条件[式(4)～式(6)],可得

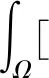
ΔWT(x,t)DiPiW(x,t)]dx=

(11)

对Vi沿着闭环系统[式(3)]的状态轨迹关于时间t求导，即

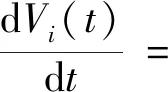
ΔWT(x,t)DiPiW(x,t)]dx+

(12)

将式(11)代入式(12),得

(13)

利用Jensen不等式：

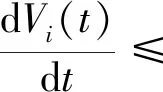
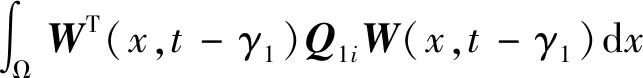
(14)

令

ηT(x,t)=[WT(x,t),WT(x,t-γ1),

那么有

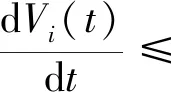
(15)

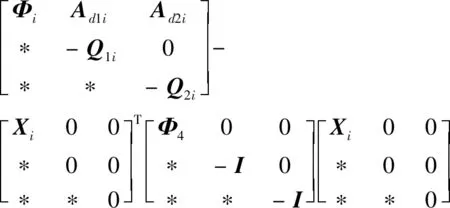
(16)

式(16)中:

(17)

利用Schur补引理,可以得到与式(8)等价的线性矩阵，即

(18)

定理2 已知具有连续分布时滞的切换分布参数系统[式(1)],其初边值条件为式(4)、式(5)。如果对于任意给定的矩阵Q1i,Q2i>0,存在矩阵Xi>0,Mi,使以下矩阵不等式成立：

(19)

当i=1时,闭环切换分布参数系统[式(3)]退化为系统：

BU(x,t)

(20)

即为文献[18]中的系统[式(14)]。由定理2容易得到。

推论1 已知系统[式(20)],其初边值条件为式(4)、式(5)。如果对于任意给定的矩阵Q1,Q2>0,存在矩阵X>0,M,使得以下线性矩阵不等式成立:

(21)

3 数值例子

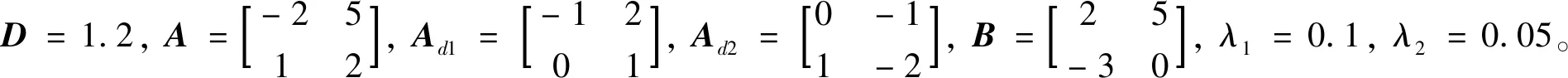
利用MATLAB解LMI(21),得到系统状态反馈增益矩阵为K=[-3.670 4 -1.166 5; -1.234 4 -4.631 5]；利用文献[18]推论1的结果得到K=[-4.654 6 -1.373 8; -1.435 9 -6.277 3]。

通过数据对比可以发现,通过本文结论获得的增益比通过文献[18]结论获得的增益数值小。说明本文通过较小增益的反馈控制能实现系统的渐进稳定,本文设计的控制器优于文献[18]。

4 结论

通过构造切换Lyapunov-Krasovskii函数,结合Poincare不等式、Jensen不等式和LMI,设计了具有连续分布时滞的切换分布参数系统状态反馈控制器和切换规则,给出了该类系统渐近可镇定的充分条件。比较已有分布参数系统相关结论,考虑了分布参数系统中Laplace算子的系数对系统的影响。所得可以看作是已有分布参数系统相关结论的推广和改进。最后,通过仿真进行了验证。