关于位移水仙花数的研究

杨健，韦佳玉，蒋剑军

（铜陵学院数学与计算机学院，铜陵244061）

0 引言

整数世界的神秘让人自小就会产生无穷的求知欲望。水仙花数是不少人初中时代播下的一颗种子，到大学时代对它的认知彻底清晰起来。所谓水仙花数是指一个3位数，它各位数字的3次方之和等于该数自身[1]。利用枚举法或计算机编程，知水仙花数共有四个：153、370、371 和 407。

寻找水仙花数，用数学语言表达就是求解下述关于x,y,z的不定方程：

其中x,y,z都是介于0到9的整数，且x≠0。

有了（1）式的数学语言，初中时代播下的求知种子，到大学时代发了芽。方程（1）是三位整数的情况，它在n位的情形是怎么样的呢？即求下述关于(n;x1,x2,…,xn)的不定方程的解（或全部解）：

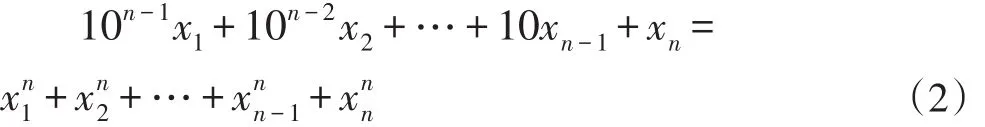
其中xi(1,2…,n)都是介于 0到 9的整数，且x1≠0。

满足方程（2）的n位正整数也称为水仙花数，它是经典的三位水仙花数往高位整数上的拓展。

众所周知，方程（2）至少有解（3;1，5，3）、（3;3，7，0）、（3;3，7，1）和（3;4，0，7）分别对应着上面所列的 4 个经典的水仙花数。当n＞3呢？查阅文献知，2002年林宣治[2]及2015年卫洪春[3]分别求出了方程（2）的所有解，即得到了所有的水仙花数，其中最大的水仙花数有39 位：115132219018763992565095597973971522401。

因为水仙花数的趣味性，以及在计算机程序设计教学中的特殊地位，近年来依然有学者将它作为各种计算机语言程序设计教学中的范例[4-8]，或做着水仙花数的科普工作[9]。

文献[2]及文献[3]对水仙花数的彻底解决并没有阻挡我们对水仙花数未知世界的探索。本文进一步将水仙花数推广为更为广阔的概念——位移水仙花数，研究该类水仙花数的性质，并设计基于MATLAB矩阵运算的快速算法求解满足一定条件的所有的位移水仙花数。

1 位移水仙花数

1.1 定义

一个n位正整数若等于它各个位上数字的n+d次方之和，则称该n位正整数为指数位移d的n位水仙花数，简称位移d水仙花数。此时称d为位移。设是一个位移d水仙花数，则下述（3）式成立：

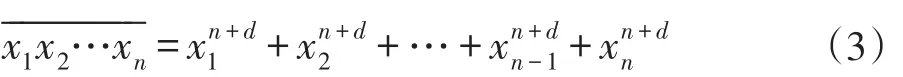
其中xi(1,2…n)都是介于0到9的整数且x1≠0。

例如，4150=45+15+55+05，故4150是位移d=1水仙花数；再如，194979=15+95+45+95+75+95，故194979是位移d=-1的水仙花数。

当d＞0,d=0,d＜0时分别称为正位移、0位移、负位移的水仙花数。易知，0位移水仙花数就是一般意义下的水仙花数。

1.2 性质

因为位移水仙花数比水仙花数多一个位移参数，所以具有丰富的性质。

性质1【有限性】设d为一给定整数，则位移d水仙花数的个数是有限的。

易得：

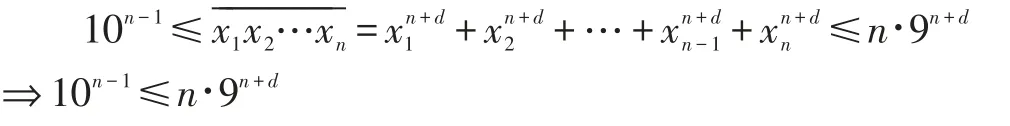
上式两边取以10为底的对数，得：

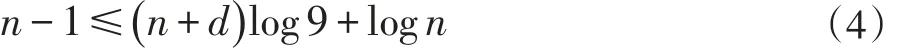
将（4）式整理为如下形式：

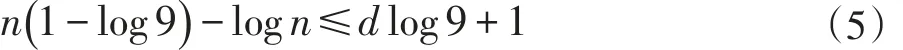
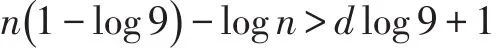
时位移d的n位水仙花数是不存在的，故位移d的水仙花数的个数是有限的。

性质2【n和d的关系性质】位移水仙花数中，位移d与位数n满足如下关系式：

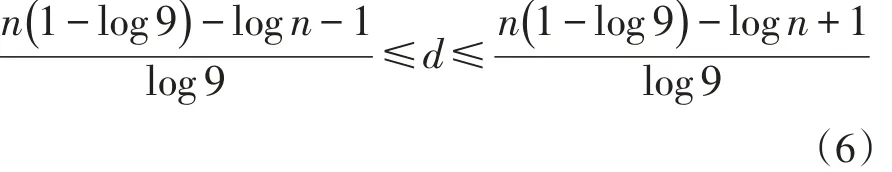
证明（6）式的左边不等式已由（5）式给出。下面证明（6）式的右边不等式。

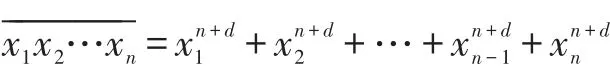
对上式右边放大后易得：

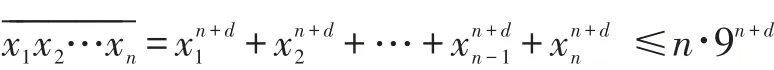
按上述放大所得的数n·9n+d，其位数至多增加1，即n·9n+d至多是n+1位整数，即：

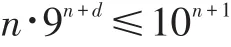
上式两边取以10为底的对数，得：

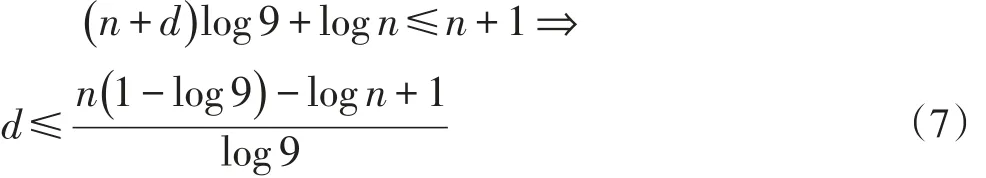
这就完成了性质2的证明。

性质2意义非常丰富。首先，（6）式可视化如下；然后，由（6）式得到d的最小值为-1；最后，由（6）式，应用MATLAB编程计算给定d对应的n值的范围如表1所示。

表1 给定d对应的n值的范围

注意，应用（6）式计算得到的n的上界和下界，并非n的上确界和下确界。例如，当d=0时，n的下确界是 1，上确界是 39（见文献[1-2]）。

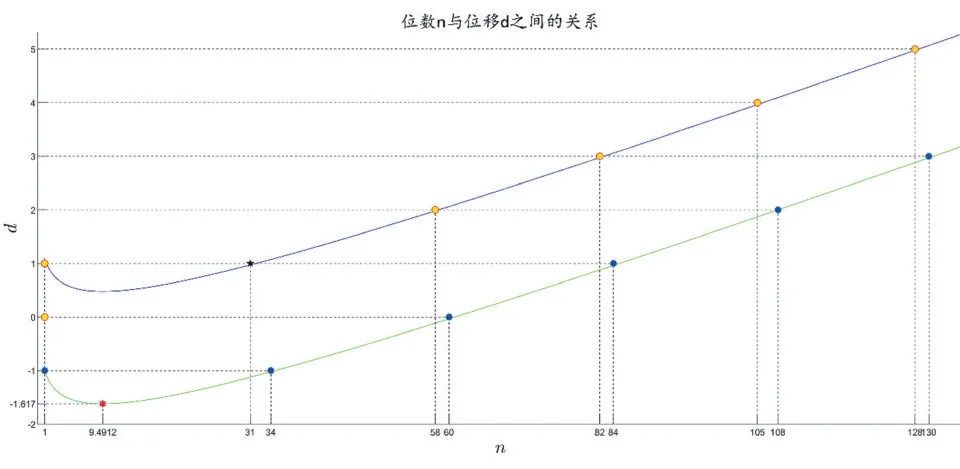
图1

在描述性质3之前，先提出并证明下面的引理。为方便描述下述引理和性质3，我们引入如下记号：

引理 1【7整除1(n)的判别】（1）；（2）当6|n时，7||1(n)。

证明：

（1）简单计算知，当n=1,2,3,4,5时，7∤1(n)；当n=6时，7|1(n)。

充分性：设6|n，可写为n=6k。则：

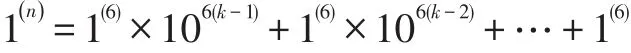
上式右端的k个加项都能被7整除，故能被7整除。

必要性：设7|1(n)。

设n=6k+r,0＜r≤6，下面证明r=6。

将1(n)改写为：

上式右端能被7整除，故左端中必有7|1(r)，从而得r=6。

（2）因为1(6)=3×7×11×13×17，即 7||1(6)，所以当6|n时，有

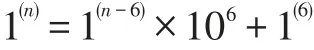
从而得7||1(n)。

注：引理1说明，7至多是1(n)的单因子。

同理可得下述两个引理。

引理2【3恰好整除1(n)的判别】3||1(n)⇔3||n。

注：引理2说明，当且仅当3||n时，3是1(n)的单因子。

引理 3【9 整除1(n)的判别】（1）；（2）当9|n时，9||1(n)。

注：引理3说明，9也至多是1(n)的单因子。

性质3【位异性】位数大于1的位移型水仙花数，至少存在两个位上的数字是互异的。

反证法。假设存在整数d(≥-1)，使m(n)得是位移d的n位水仙花数，即：

注意到，m(n)=m·1(n)，结合上式得：

显然，（8）式中m≠1,5且m不能为偶数。于是m只可能是 3、7、9。

经检验，（8）式右端n+d-1≥2，故若m是 3、7、9之一，则必然有m是1(n)的至少2重因子，这矛盾于上面的三个引理。

性质3说明，位数大于1的各位数字相同的正整数不会是位移型水仙花数，从而不会是水仙花数。这是下述性质4的基础。

性质4【惟一性】设某个n位的位移d水仙花数从高位到低位的数字依次是x1,x2,…,xn，则这n个数字的其他任意异于x1x2…xn的排列所成的n位正整数都不是位移d水仙花数。

证明：

设x1,x2,…,xn是位移d的n位水仙花数从高位到低位的数字，xi1,xi2,…,xin（其中xi1≠0）是x1,x2,…,xn的异于x1,x2,…,xn的一个排列，令：

因为xi1,xi2,…,xin和x1,x2,…,xn互异的两个排列，必然有A≠B。

因为A是位移d的水仙花数，故：

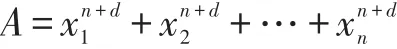
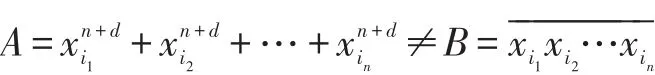
故B不是位移d的水仙花数。

3 算法实现

3.1 算法设计

计算泛水仙花数，计算量超大是其特点。所以在设计基于MATLAB快速计算泛水仙花数的算法方面，须充分考虑MATLAB的计算特点。众所周知，MAT⁃LAB计算特点是数据以矩阵为单元，循环效率相对较低。所以在设计算法时必须将输入、输出和存储数据都矩阵化，降低对循环的依赖，以提高效率。本文正是基于MATLAB擅长矩阵运算的特点设计算法以计算位移型水仙花数。算法描述如下。

算法：基于MATLAB的计算位数不超过len、位移为d的所有水仙花数的矩阵算法

毋庸讳言，本算法有很大的局限，并不能应对任意位数的水仙花数的求解。

3.2 计算结果

由d与n的关系图知，d=-1的位移水仙花数最高位不超过34位，实际最大值为8，一共有2个：194979，14459929；d=1的位移水仙花数最高位不超过84位，因为个人电脑算力的原因，本文计算了10位以内的所有d=1的位移水仙花数，获得两个该类水仙花数：4150，4151；d=2的位移水仙花数位数最小为58，最大为108，本文没能计算得到该类水仙花数；更大的位移已没有计算能力应对。

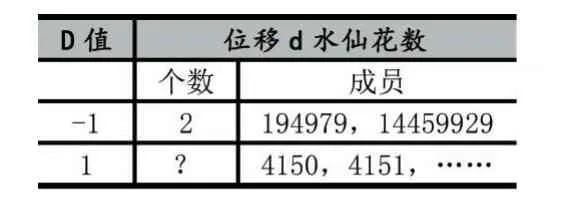
表2 计算结果

4 水仙花数的分类

现在我们将位移型水仙花数简称为水仙花数，它包括了一般意义上的水仙花数（即3位经典水仙花数和高位水仙花数），那么对水仙花数的描述有2个特征：位数n和位移d；进而对水仙花数的分类就可按位数n分类或按位移d分类。那么，按哪个特征分类更好呢？我们认为按位移分类更好，因为，简单的枚举计算就知道n=2时没有的任何位移的水仙花数。目前计算得到的结果按d分类如表3。

即位移-1的水仙花数有2个，位移0的水仙花数有88个，位移1的水仙花数最高位不超过84，计算得到10位以内有2个。需要说明的是，由于1的特殊性，我们不将1视为任何位移的水仙花数。

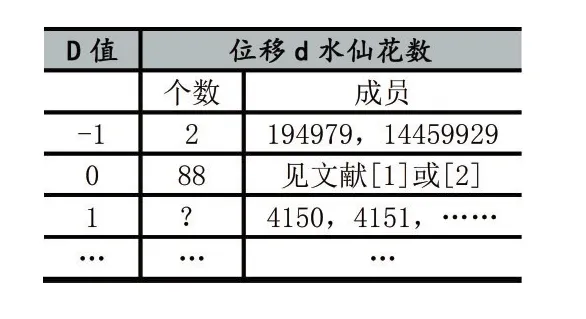
表3 水仙花数的分类

5 结语

本文首先将水仙花数推广为更一般的位移水仙花数，使得水仙花数成为我们研究范畴的一个特例。为了实际上讨论和描述的方便，本文可以从一开始就称呼位移水仙花数为水仙花数。然后对水仙花数的性质进行了比较细致的研究，得到的性质既是水仙花数的特征，也十分有趣。最后对水仙花数的分类进行了一些讨论。在对水仙花数分类的过程中，不禁产生了一些疑惑，其中最大的疑惑就是：

问题1是否存在任意位移的水仙花数？

显然，无论计算机技术发展到什么程度都无法从计算的角度解决上述问题。于是，我们把上述问题等价地转化为如下数学问题：

问题2下述关于(n;d,x1,x2,…,xn)的不定方程：

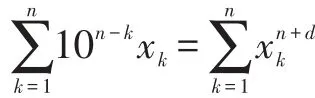
的解是否是有限的？其中0≤xk≤9,k=1,2,…,n，且x1≠0。

期待数学工作者给出问题2的解答。