一类具有饱和发生率和心理作用的随机SIR传染病模型

赵彦军, 李辉来, 李文轩

(1. 东北师范大学人文学院 数学系, 长春 130117; 2. 吉林大学 数学学院, 长春 130012)

0 引 言

微分方程的数学模型在描述动态行为方面具有重要作用, 广泛应用于生物学、 物理学和医学等领域. 为控制传染病的传播, 通常通过建立数学模型研究传染病的动力学行为. Kermack等[1]首次提出了传染病仓室模型的“阈值理论”, 为传染病动力学的研究奠定了基础. 目前, 对传染病模型的阈值动力学行为研究已有许多成果. Capasso等[2]通过研究如下确定性SIS传染病模型：

(1)

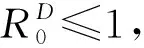
其中:S(t)表示t时刻易感者数量,I(t)表示t时刻传染者数量, 且N=S(t)+I(t);β表示疾病的接触率;μ表示疾病的死亡率;γ表示疾病的恢复率.

(2)

其中，B(t)是定义在完备概率空间(Ω,F,P)上的标准布朗运动，σ表示高斯白噪声的强度. 文献[5]得到了系统(2)全局阈值动力学行为的结果.

尽管在经典传染病模型中, 双线性发生率被广泛使用, 但在高传染水平下, 由于心理作用和社会因素的影响, 易感者减少与感染者接触和防护措施的增强, 使易感者和感染者间的有效接触率会趋于饱和状态. Capasso等[2]在研究意大利巴里爆发霍乱时最早提出了具有饱和效应的非线性发生率, 得到了与实际情况吻合的结果, 此后各种非线性饱和发生率被广泛应用于传染病模型研究中, 均得到了较好的结果.

本文在系统(2)的基础上, 进一步考虑疾病爆发过程中“心理作用”导致饱和效应发生率的随机SIR传染病模型：

(3)

(4)

易得

d(S(t)+I(t))=[μN-μ(S(t)+I(t))-(δ+ν)I(t)]dt≤[μN-μ(S(t)+I(t))]dt,

则

S(t)+I(t)≤N+e-μt(S(0)+I(0)-N).

因此Γ={(S,I):S(t)>0,I(t)>0,S(t)+I(t)≤N}是系统(4)的正向不变集.

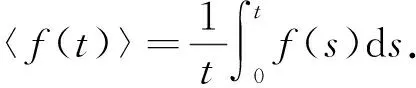
1 系统正解的存在唯一性

根据文献[6-7], 本文给出如下定理.

定理1对任意初值(S(0),I(0))∈Γ, 随机系统(4)均存在唯一正解(S(t),I(t))(t≥0), 且该解依概率1位于Γ中.

证明： 显然, 随机系统(4)的系数局部Lipschitz连续, 则对任意给定初值(S(0),I(0))∈Γ, 系统(4)存在唯一的局部正解(S(t),I(t))∈Γ,t∈[0,te), 即S(t)+I(t)≤N,t∈[0,te) a.s., 其中te为爆破时间, 要证明解的全局存在性, 只需证明te=∞ a.s.

设η0>0且满足S(0)>η0,I(0)>η0, 对任意η≤η0(η>0), 定义停时

tη=inf{t∈[0,te):S(t)≤η或I(t)≤η}.

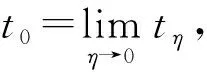
考虑如下Lyapunov函数:

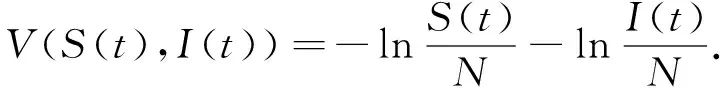
(5)

由于(S(t),I(t))∈Γ, 显然V(t)正定. 对式(5), 由It公式得其中

所以

(6)

对式(6)两端分别从0到tη∧T积分并取期望, 得

EV(S(tη∧T),I(tη∧T))≤V(S(0),I(0))+KE(tη∧T)≤V(S(0),I(0))+KT.

其中IΩη是Ωη的示性函数. 令η→0, 可得矛盾: ∞>V(S(0),I(0))+KT=∞. 所以t0=∞ a.s., 表明(S(t),I(t))以概率1在有限时间内不会产生爆破. 证毕.

2 疾病灭绝性的充分条件

证明： 设(S(t),I(t))是系统(4)满足初值(S(0),I(0))∈Γ的解, 对系统(4)应用It公式, 有

(7)

对式(7)两边从0到t积分, 有

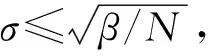
证明： 对式(7)两边从0到t积分, 有

对式(9)两端取上确界的极限, 有

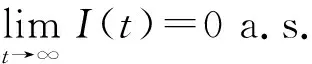
定理2和定理3表明, 当白噪声扰动较大或R*≤1且白噪声扰动不大时, 疾病即灭绝.

3 疾病在均值意义下的持久性

定理4设(S(t),I(t))是系统(4)关于初值(S(0),I(0))的解, 若R*>1, 则系统(4)的疾病将持续存在, 且满足

Θ(t)=μN-μ〈S(t)〉-(μ+δ+ν)〈I(t)〉,

对式(10)从0到t积分, 有

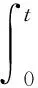
当R*>1, 可得

证毕.

定理4表明, 当白噪声扰动足够小, 使得R*>1时, 疾病将持续存在.

4 数值模拟

下面基于文献[6-8,10-16]的模拟数据, 利用MATLAB工具进行数值模拟, 以验证本文结论的正确性. 根据Milstein方法, 利用MATLAB对具有饱和发生率和心理作用的随机SIR传染病系统(4)进行模拟, 系统(4)的离散格式如下：

其中ξk(k=1,2,…,n)是独立的标准正态随机变量.

1) 取N=10,μ=0.2,β=0.06,α=1.6,γ=0.05,θ=0.05,σ=0.1,δ=0.000 1,ν=0.001,S(0)=21,I(0)=4, 使得R*=0.332 1≤1, 且满足定理2的条件. 由定理2可知, 此时疾病将趋于灭绝, 模拟结果如图1所示.

图1 当环境扰动较大且R*≤1时, S(t),I(t)随时间的变化曲线Fig.1 Change curves of S(t) and I(t) with time whenenvironmental disturbance is large and R*≤1

2) 取N=10,μ=0.2,β=0.06,α=1.6,γ=0.05,θ=0.05,σ=0.077 46,δ=0.000 01,ν=0.000 01,S(0)=21,I(0)=4, 使得R*=1.000 1>1, 且满足定理2的条件. 由定理2可知, 此时疾病将趋于灭绝, 模拟结果如图2所示.

图2 当环境扰动较大且R*>1时, S(t),I(t)随时间的变化曲线Fig.2 Change curves of S(t) and I(t) with time when environmental disturbance is large and R*>1

对比图1和图2可见, 无论R*小于等于1还是大于1, 只要满足定理2的条件, 系统(4)的疾病均趋于灭绝, 与定理2的结论相符.

3) 取N=10,μ=0.2,β=0.065,α=1.6,γ=0.05,θ=0.05,σ=0.055,δ=0.1,ν=0.1,S(0)=21,I(0)=4, 使得R*=0.997 5≤1, 且满足定理3的条件. 由定理3可知, 此时系统(4)的疾病将趋于灭绝, 与定理3的结论相符, 模拟结果如图3所示.

图3 当环境扰动较小且R*≤1时, S(t),I(t)随时间的变化曲线Fig.3 Change curves of S(t) and I(t) with time when environmental disturbance is small and R*≤1

4) 取N=10,μ=0.2,β=0.065,α=1.6,γ=0.05,θ=0.05,σ=0.035,δ=0.000 1,ν=0.001,S(0)=21,I(0)=4, 使得R*=1.955 3>1, 且满足定理4的条件. 由定理4可知, 此时系统(4)的疾病将持续存在, 与定理4的结论相符, 模拟结果如图4所示.

图4 当环境扰动较小且R*>1时, S(t),I(t)随时间的变化曲线Fig.4 Change curves of S(t) and I(t) with time when environmental disturbance is small and R*>1

综上所述, 本文研究了一类利用白噪声描述环境对疾病传播影响的随机SIR传染病模型, 得到了模型全局正解的存在唯一性、 灭绝性和持续存在性, 并通过数值模拟验证了所得结果的正确性.