铁路隧道防灾通风射流风机安装位置对通风效果的影响

赵东平，温斯逊，杨柏洪

（1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031）

随着我国铁路隧道逐渐向长大、深埋方向发展，隧道的防灾救援问题日益突出。防灾通风系统是隧道防灾救援体系中的重要组成之一，在隧道防灾救援工作中发挥着重要作用，是事故工况下人员安全疏散的重要保障。根据现行《铁路隧道防灾救援疏散工程设计规范》［1］要求，在铁路隧道紧急出口及隧道口救援站内均应设计防灾通风系统，一旦长大隧道或隧道群内发生火灾或其他事故，列车驶往紧急出口或隧道口救援站进行疏散时，应开启救援疏散设施内的防灾通风系统，维持辅助坑道向隧道正洞的风压。

目前，我国铁路隧道相关救援设施内安装的防灾风机以射流风机为主，根据其工作原理可知，射流风机与防护门之间的距离会直接影响射流通风效果。为了改进射流风机的通风效果，我国学者已经开展了大量相关研究，赵黎等［2］对2 车道公路隧道内的射流风机空间安装布局进行了研究，分析了风机的纵、横向间距以及布置高度等参数对通风效果的影响。张恒等［3］对隧道施工通风中风机布置位置对通风效果的影响进行了分析研究，提出了通风管在隧道横断面上的布置方式，以及风管出风口与隧道掌子面的距离建议值。王松等［4］利用Fluent程序对公路隧道内射流通风速度场及压力场进行了模拟分析，得出了风机主射流范围。曹正卯等［5］通过CFD 模拟与理论分析相结合的方法，以关角隧道为工程依托，研究了铁路隧道运营期间，多种射流风机组合布置形式对通风效果的影响。赵东平等［6］以某铁路隧道紧急救援站为工程依托，研究了风机布置于正洞、横通道及同时布置于正洞及横通道内3种方案对于通风效果的影响。王骏横等［7］对隧道内风机布置方式对隧道横断面风速的影响进行了研究，结果表明当风机均匀分布于横断面时，能够在更短距离内产生均匀程度较高的断面风速。范建国等［8］利用CFD 软件对双车道公路隧道内射流风机组合效果进行了模拟，得出了2 台风机组合时横向以及纵向的最佳距离。方勇等［9］利用Flu⁃ent 软件建立隧道三维模型，研究了风管出口位置对公路隧道施工通风效果的影响，认为风管距离工作面越近，射流速度变化梯度越大，通风效果越明显，并且造成的局部压力损失也越大。喻映华等［10］对射流风机安装在隧道紧急停车带扩大断面的流场进行了三维数值模拟，分析了隧道气流速度和压力的分布规律。姜学鹏等［11］通过理论分析与数值模拟相结合的方法研究了隧道内自然风对射流风机临界风速的影响。王峰等［12］通过三维数值模拟，分析了小半径曲线隧道射流风机布置方式对风机升压折减效率的影响。温玉辉等［13］采用CFD程序对射流风机的升压效率影响因素进行了三维数值分析，确定了影响射流风机升压效率的主要因素并提出提高射流风机升压效率的措施。

从既有文献来看，现阶段关于隧道射流风机通风领域的研究主要集中于3个方面：一是，针对公路隧道运营阶段的射流通风效率及风机布置优化等问题的研究；二是，针对隧道施工过程中，射流通风效率、风机布置方式及风管与掌面的距离等问题的研究；三是，针对长大铁路隧道防灾工况下射流风机通风效果的研究。相比前2 个方面，在第3 个方面的研究成果明显偏少，尤其是对铁路隧道防灾通风中射流风机安装位置与通风效率相关性的研究，更是未见诸报道。

本文以湘渝高速铁路某隧道口救援站为依托工程，对隧道口救援站及横洞式紧急出口射流通风开展研究，分析隧道口救援站内风机安装位置对通风效果的影响，以及单车道、双车道辅助坑道断面条件下，横洞式紧急出口内射流风机与防护门之间距离对通风效果的影响，进而确定防灾通风射流风机最佳安装位置，以期为铁路隧道防灾通风射流风机的安装提供参考。

1 依托工程概况

湘渝高速铁路某隧道群全长约21.0 km，由2座隧道组成，其中隧道A 全长13.4 km，隧道B 全长7.4 km，隧道之间由1 座全长218 m 的大桥相连。为解决隧道群防灾救援问题，在2 座隧道进出口之间设有隧道口救援站1座，救援站全长726 m，其中明线段218 m，伸入隧道A 段254 m，伸入隧道B 段254 m。隧道口救援站的平面布置如图1 所示，深入隧道B的部分及辅助坑道的平面布置如图2 所示，图中的数字编号表示不同位置的防护门编号。

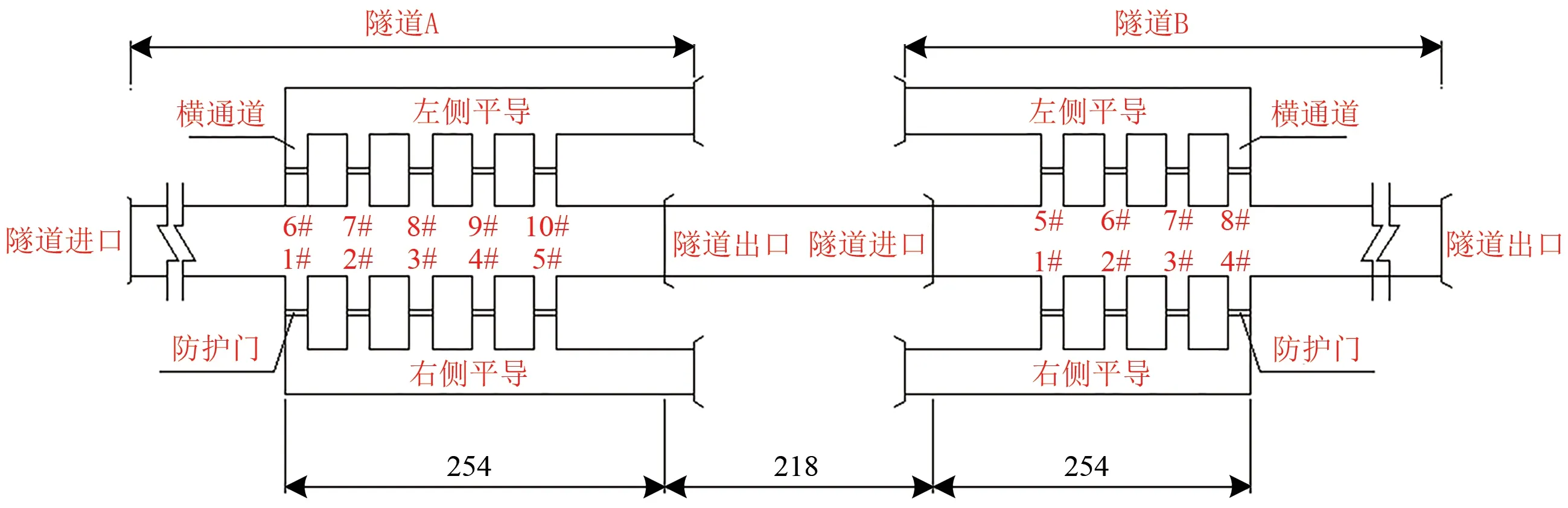
图1 某隧道口救援站平面示意图（单位：m）

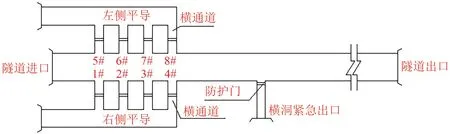
图2 隧道B救援站及辅助坑道布置示意图

2 射流通风理论基础

隧道射流通风，本质上是流体流动的过程，遵循着物理学三大定律：质量守恒定律（连续性方程）、动量守恒定律（Navier-Stokes 方程）、能量守恒定律（能量方程）［14］。

1）连续性方程

隧道内的空气应遵循质量守恒定律，可用质量守恒方程表示为

式中：ρ为流体密度；t为时间；u，v，w分别为流体沿x，y，z方向的速度矢量。

2）Navier-Stokes方程

隧道内射流通风过程中，x，y，z这3 个方向都应满足动量守恒方程，3 个方向的动量守恒方程分别如下。

x方向为

y方向为

z方向为

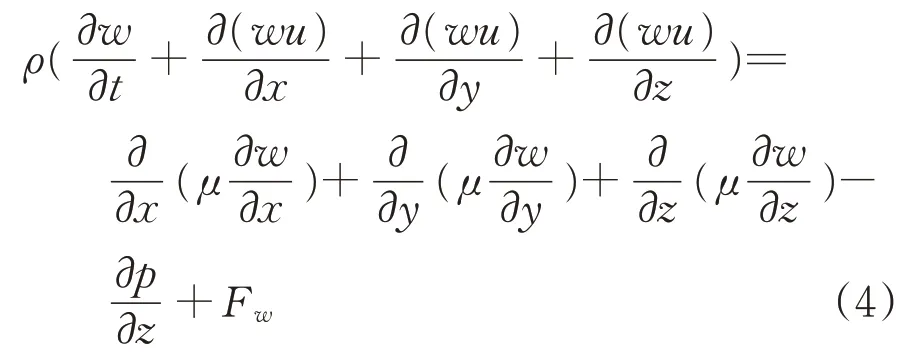
式中：μ为动力黏度；p为压力；u，v，w分别表示气体沿x，y，z方向的流动速度；Fu，Fv，Fw分别为x，y，z方向单位体积流体受的外力。

3）能量方程

射流风机出口气流与伴随流发生热交换必须遵守能量守恒定律，可用式（5）求得空间任一点的温度［14］。

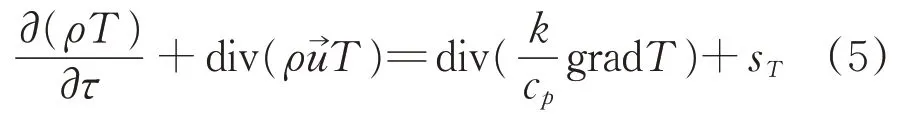
式中：cp为流体比热容；sT为能量源项；T为温度；为速度矢量。

3 隧道防灾通风射流风机配置计算

为满足长大铁路隧道在防灾工况下的通风要求，需要在隧道紧急出口处及隧道口救援站内配置相应的风机。考虑到射流风机安装方便、便于维护等特点，本文采用目前业内普遍采用的射流风机通风方案。

确定射流风机的具体配置时，不但需要隧道正洞及辅助坑道的长度、平面布置及断面面积等参数，还需根据隧道平面布置建立网络通风模型，代入拟定风机参数并迭代计算，最终求解得到满足防护门处风速要求的射流风机最佳配置方案及其具体型号。

3.1 隧道紧急出口处的射流风机配置

1）网络通风模型和计算参数

针对湘渝高速铁路某隧道群隧道B的紧急出口部分，先将隧道正洞、辅助坑道及横向联络通道抽象成由边及节点组成的通风网络，再利用SES 软件建立网络通风模型，具体如图3所示。图中分支1、分支2表示隧道正洞的2段；分支3表示辅助坑道，箭头表示初始假定的风流运动方向。

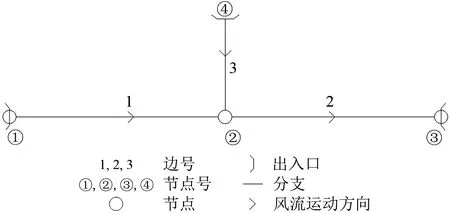
图3 紧急出口通风网络

模型计算参数见表1，其中分支3-1 和分支3-2 分别对应辅助坑道为单车道和双车道2 种断面工况。表中长度、断面积、断面周长等参数均可根据隧道设计资料获取，沿程阻力系数及分支两端的局部阻力系数（表中正向对应于假定的风流方向，负向对应于与假定风流相反的方向）可根据《铁路隧道运营通风设计规范》附录B 选取［15］，局部阻力系数的计算方法参考文献［6］。

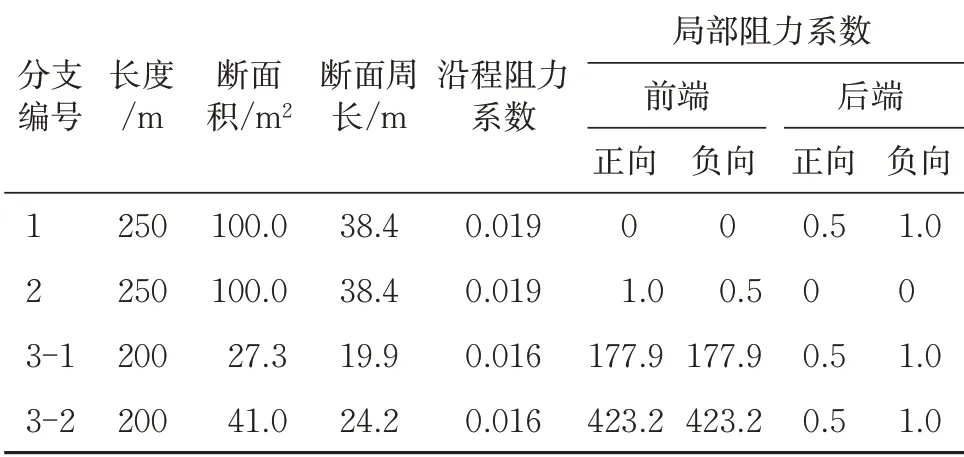
表1 紧急出口网络通风模型计算参数

2）射流风机性能参数

根据工程经验，拟选取SDS63T-2P-5.5 型射流风机进行网络通风计算迭代。风机放置于紧急出口的横洞内，具体性能参数整理见表2。

表2 紧急出口射流风机性能参数

3）射流风机配置计算结果

《铁路隧道防灾疏散救援工程设计规范》中规定：防灾通风工况下，紧急出口内防护门处的风速不得小于1.5 m·s-1。采用网络通风算法，经SES程序计算可知，在单车道、双车道的辅助坑道内各安装1 台SDS63T-2P-5.5 型射流风机，便可满足规范对风速的规定。此时，各分支的风速计算结果见表3。表中风速的负值表示计算的风速方向与初始假定相反。

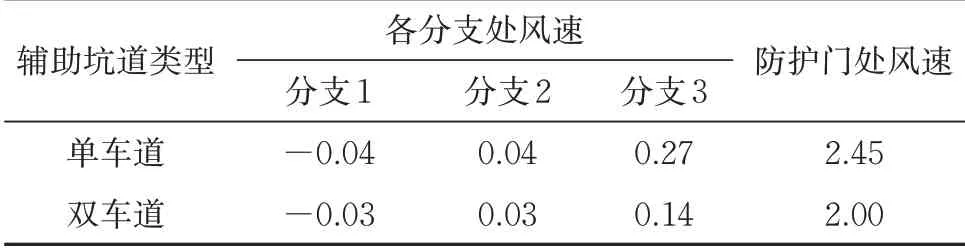
表3 紧急出口辅助坑道、隧道正洞及防护门处风速计算结果 m·s-1

3.2 隧道口救援站的射流风机配置

1）网络通风模型和计算参数

考虑本线路为设计速度350 km·h-1的高速铁路，根据《铁路隧道防灾疏散救援工程设计规范》，取隧道火灾规模为15 MW。利用SES软件建立的隧道口救援站网络通风模型如图4 所示。图中，分支1—分支7表示隧道正洞区段；分支8—分支11 表示隧道口救援站辅助坑道区段；分支12—分支15 表示隧道正洞与辅助坑道之间用于人员疏散的横向联络通道；箭头表示模型初始假定的风流运动方向。

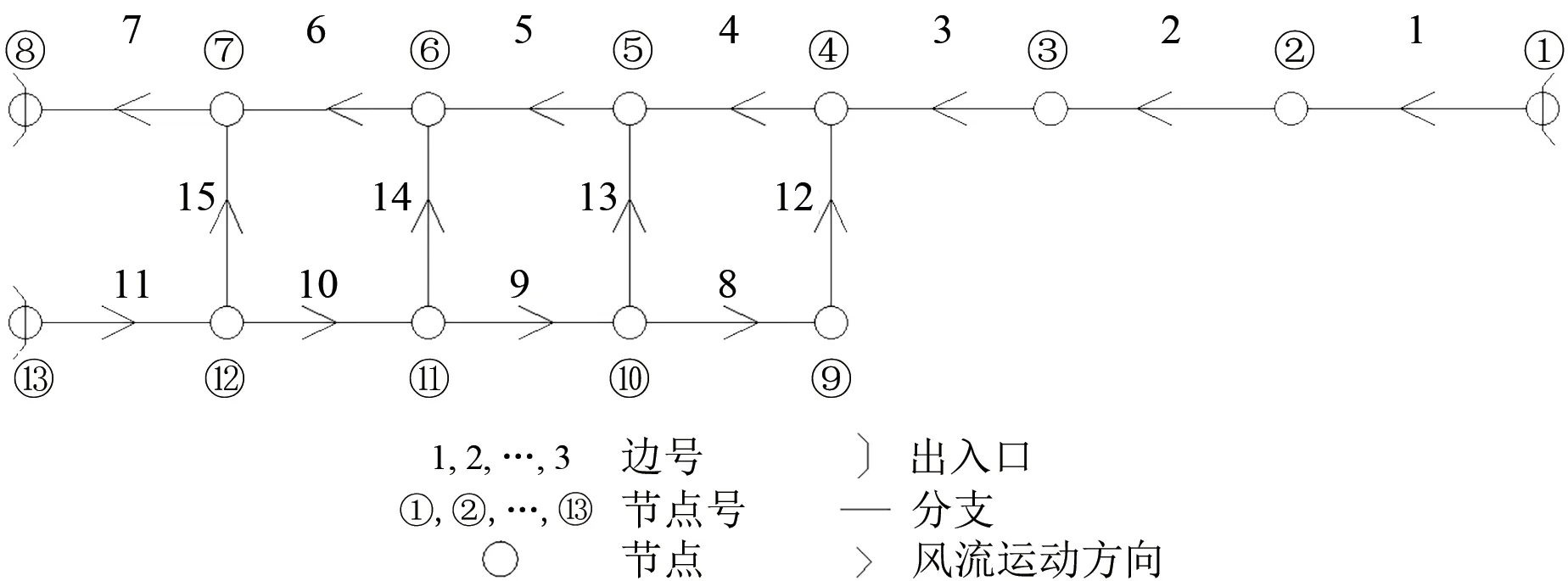
图4 隧道口救援站通风网络图

该网络通风模型计算参数见表4，具体获取与计算方法同紧急出口网络通风计算参数。

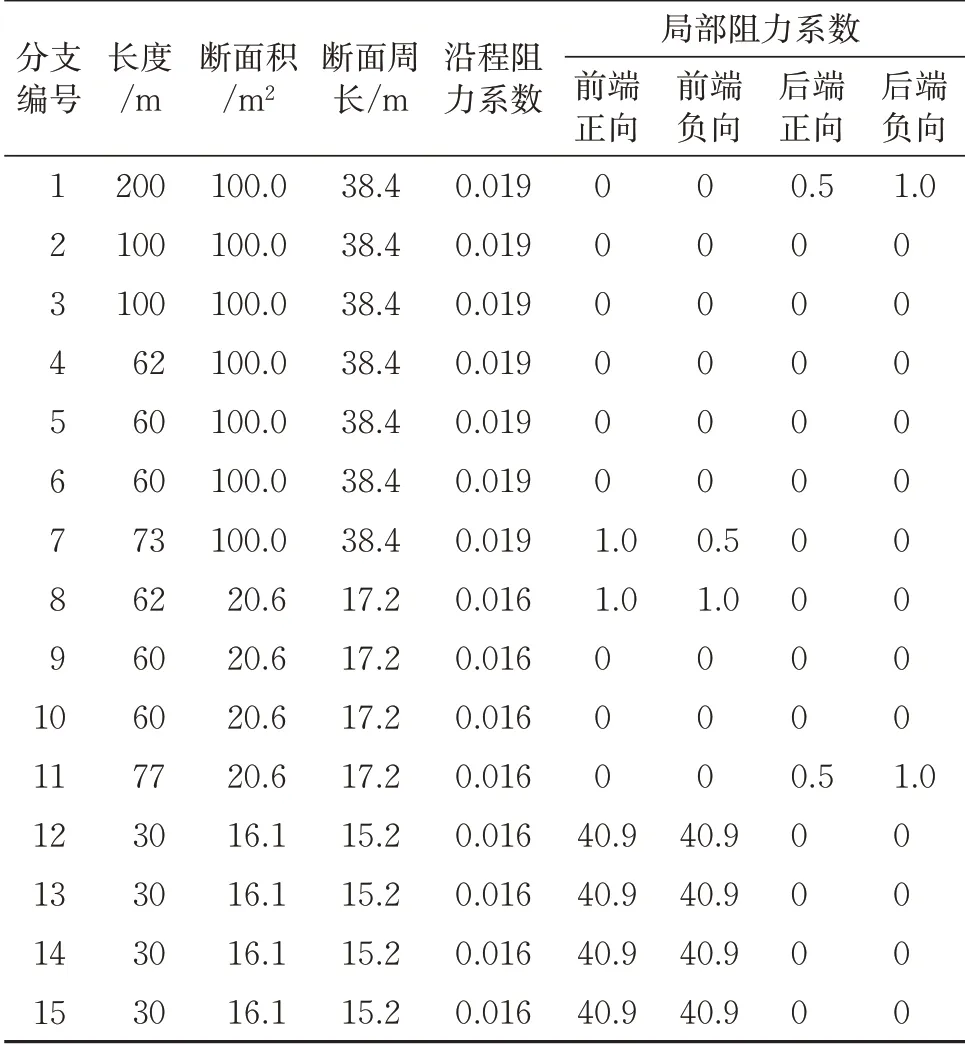
表4 隧道口救援站通风网络计算参数

2）射流风机性能参数

根据工程经验，拟选取2 种类型的射流风机进行网络通风计算迭代。分别是：SDS125T-4P-90型风机，在隧道口救援站伸入隧道正洞的区域内配置2 台；SDS63T-2P-15 型风机，在隧道口救援站平导内配置1 台。2 种射流风机的性能参数整理见表5。

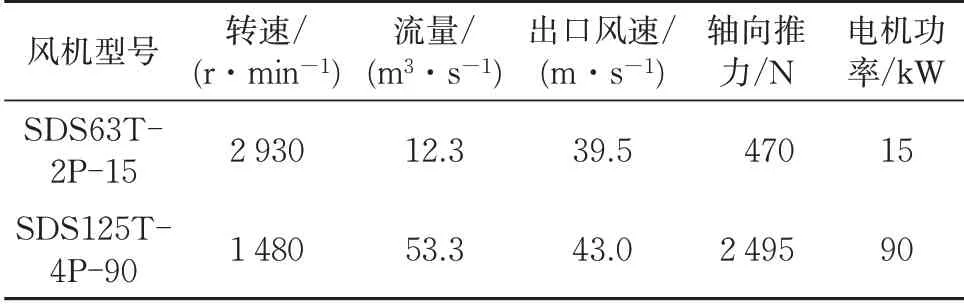
表5 救援站射流风机性能参数

3）射流风机配置计算结果

《铁路隧道防灾疏散救援工程设计规范》中规定：防灾通风工况下，隧道口救援站内防护门处的风速不得小于2.0 m·s-1；隧道口救援站内隧道出口处风速不应小于1.5～2.0 m·s-1，风向由洞内吹向明线段。《铁路隧道运营通风设计规范》规定，通风计算尚应考虑自然风影响［15］。因此此处考虑的计算工况为：隧道正洞自然风风速为2.0 m·s-1（风向吹向隧道进口），火源分别位于分支4—分支7及洞外。

采用网络通风算法，经SES 程序计算得到隧道口救援站的射流风机配置型号，在救援站伸入隧道正洞的区域内配置2台SDS125T-4P-90型风机，在隧道口救援站平导内配置1台SDS63T-2P-15型风机，便可满足规范对风速的规定。此时，救援站隧道出口区段正洞内风速及各防护门处风速的计算结果，整理见表6。

表6 救援站出口正洞及防护门处风速计算结果m·s-1

由表6 可知：在拟定的风机配置情况下，当火源位于不同分支时，各个防护门处最小风速为2.71 m·s-1，隧道口救援站范围的隧道正洞内最小风速为4.48 m·s-1，均满足防灾工况下最低通风风速的要求。

4 射流风机安装位置

网络通风算法虽然能够求解得到满足防护门处风速要求的风机配置，但其也存在将风机位置简化处理的局限性。在网络通风算法建立起的一维模型中，不管风机在隧道某分支上的位置如何变化，整个模型网络的计算结果都是相同的，这样一来，就无法判断出射流风机位置细微变化对通风效果的影响。为此，有必要采用三维数值算法，针对射流风机的安装位置开展进一步的研究。

4.1 数值模型

1）隧道紧急出口处的数值模型

依托湘渝高速铁路某隧道群，利用有限元软件STAR-CCM+建立隧道紧急出口处的数值模型，如图5 所示。参数取值：隧道正洞长度500 m，隧道中部辅助坑道长度200 m；正洞采用时速350 km·h-1双线隧道标准断面，辅助坑道分别采用单车道和双车道2 种断面；根据设计资料，辅助坑道内防护门距离正洞交叉点10 m；模型有限元网格采用多面体网格，网格最小尺寸为0.5 m，计算区域内网格单元总数为703 389个。

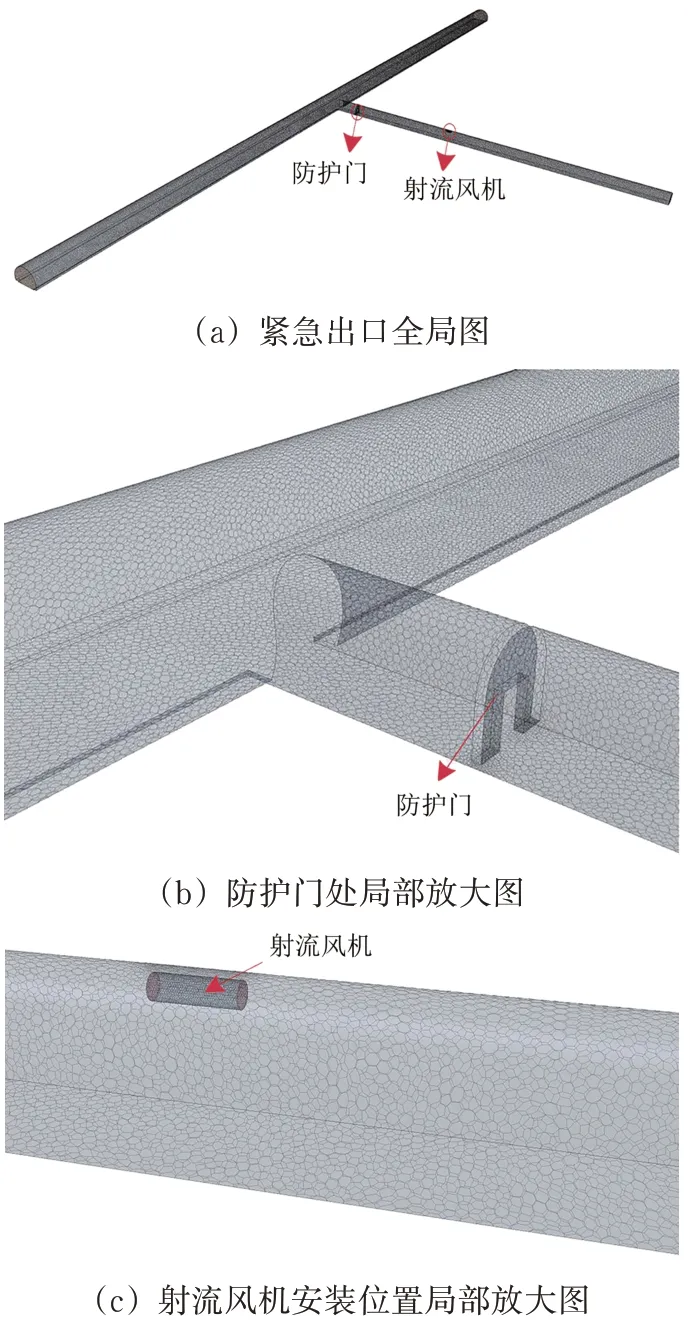
图5 隧道紧急出口数值模型

按前述风机配置计算结果，采用的风机布置为：在紧急出口辅助坑道内设置SDS63T-2P-5.5型射流风机1 台。该型风机长3.07 m，直径0.80 m，风机圆心与隧道顶部距离为1.10 m，其他具体性能参数见表2。在单车道、双车道2 种断面下，风机的具体安装位置如图6所示。

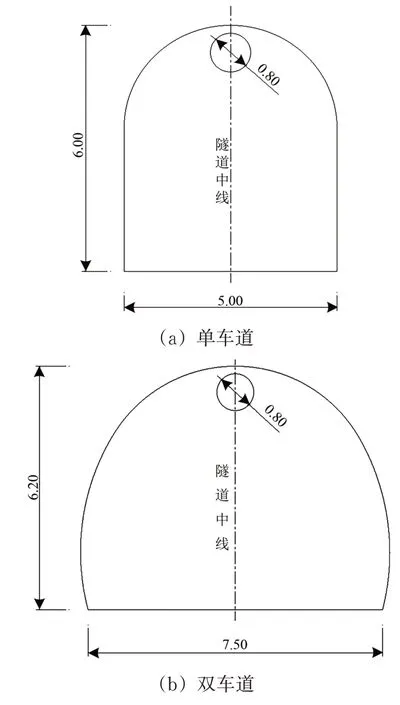
图6 辅助坑道内风机安装位置示意图（单位：m）

为研究射流风机安装位置对隧道紧急出口防护门处风速的影响，以风机与防护门之间的距离为变量，通过改变射流风机的安装位置，考察风机位置对防灾通风效果的影响。

2）隧道口救援站的数值模型

考虑到事故列车停靠在救援站时，仅开启1 侧防护门，因此，根据前述依托工程相关设计参数，以右侧平导开启防护门为条件，建立隧道口救援站三维数值模型如图7所示。参数取值：救援站模型中隧道正洞长度为655 m，救援平导长度为259 m，平导与正洞之间由长度为30 m，间隔为60 m 的4座横向联络通道连接。模型有限元网格采用多面体网格，网格最小尺寸为0.8 m，计算区域内的网格单元总数为355 401个。

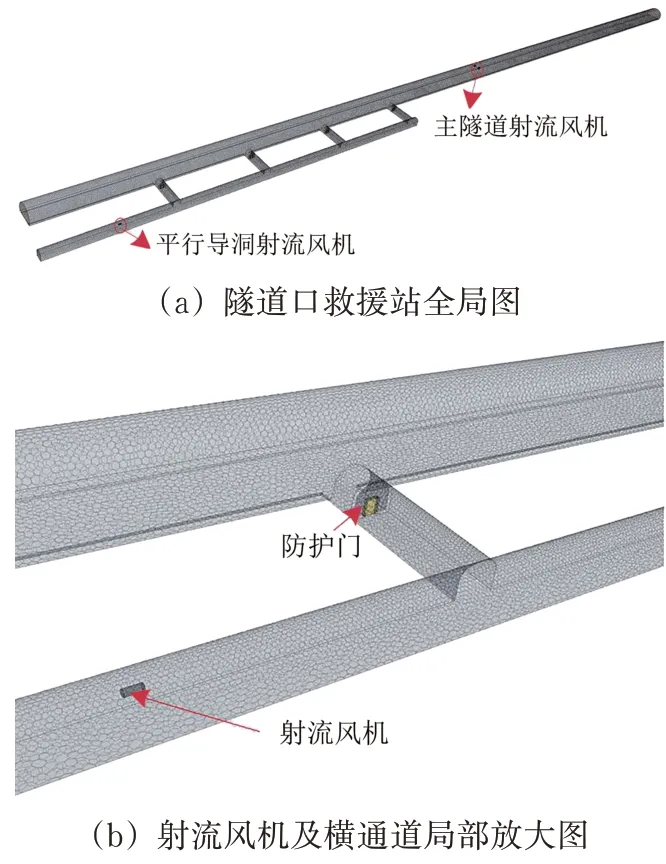
图7 隧道口救援站数值模型

按前述风机配置计算结果，采用的风机布置为：在隧道正洞内距离最后一处联络通道100 m处，安装SDS125T-4P-90 型射流风机2 台；在救援站平导内，安装SDS63T-2P-15 型射流风机1台。2 个型号风机的其他具体性能参数见表5，射流风机在横断面上的安装位置如图8所示。

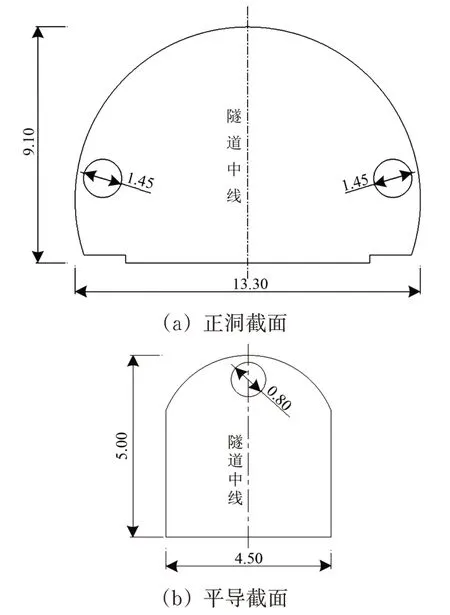
图8 救援站内风机安装位置示意图（单位：m）

为研究射流风机安装位置对隧道口救援站防护门处风速的影响，以射流风机与第1个横向联络通道的距离为变量，通过改变射流风机的安装位置，考察救援站内各个防护门处风速变化情况。

3）边界条件

数值模型中主要设置3 种边界条件，分别是速度入口（velocity-inlet）、压力出口（pressure-outlet）及壁面边界（wall）条件。

（1）速度入口。射流风机进风口和射流风机出风口均设置为速度入口边界条件，根据风机性能参数，紧急出口模型中设定风机进风口速度为-26.0 m·s-1，设定出风口速度为26.0 m·s-1；救援站模型中设定正洞内风机进风口速度为-43.0 m·s-1，出风口速度为43.0 m·s-1，平导内风机进风口速度为-39.5 m·s-1，出风口速度设置为39.5 m·s-1。

（2）压力出口。隧道出口、隧道入口、横洞出口及平导出口均设置为压力出口边界条件，相对压力设置为0 Pa，温度设置为20 ℃。

（3）壁面边界。隧道壁面以及风机壁面均设置为壁面边界条件，温度设为20 ℃。

4.2 计算工况

为了研究射流风机安装位置对其通风效率的影响，以射流风机安装位置与防护门之间的距离为变量，设计系列计算工况。考虑到火风压仅对临界风速产生影响，而对射流风机的通风效率影响有限，因此，在分析设射流风机安装位置时未考虑火灾。

在隧道紧急出口处的数值模型中，通过改变射流风机在辅助坑道内安装位置，建立不同工况，分析在各工况下开启射流风机时，辅助坑道内防护门处断面平均风速值，进而得出风机安装位置的建议值。

在隧道口救援站的数值模型中，通过改变射流风机与主隧道出口侧最近的横向联络通道距离，建立不同工况，分析各个工况下风机移动时，各个防护门处风速的变化规律，进而得出风机安装位置的建议值。

各工况下射流风机的安装位置计算结果，整理见表7。表中：D1为单车道辅助坑道断面当量直径，D1=5.49 m；D2为双车道辅助坑道断面当量直径，D2=6.78 m；D3为救援站平行导洞断面当量直径，D3=4.79 m。距离的负值和正值分别表示风机安装在第1个横向联络通道左侧和右侧。

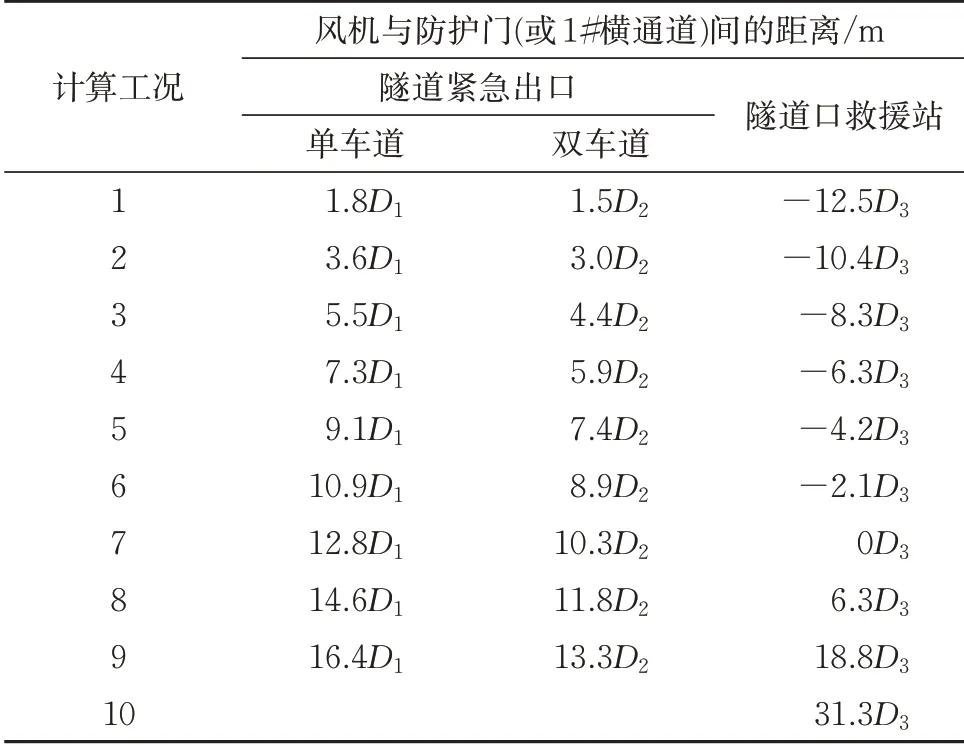
表7 不同工况时的射流风机安装位置

4.3 计算结果

4.3.1 单车道辅助坑道内射流风机安装位置

射流风机安装于单车道辅助坑道断面内，当射流风机与防护门之间的距离不同时，以辅助坑道中线截面风流速度分布为研究对象，分析风流速度场，研究断面在紧急出口数值模型中的具体位置，如图9所示。绘制各工况下辅助坑道内的风速云图如图10所示。

图9 辅助坑道风速研究截面位置

由图10 可知：射流风机工作时，其出风口端与防护门之间会产生1段风速加速段，由于加速段内风压不平衡，会在加速段形成回旋，随后断面内风速开始下降至隧道平均风速，该计算结果与文献［16］得出的结论一致；当射流风机与防护门距离在1.8D1～9.1D1之间时，风机喷射出的高速射流未发展完全，风流处在回旋段时即撞向防护门处端墙，此时射流损失较大；当风机与防护门距离为10.9D1时，射流发展段刚好充分发展，回旋段未与防护门截面相遇，风流穿过防护门截面时造成的局部损失达到最小值；当风机与防护门距离大于10.9D1时，风流加速段均得到充分发展。

当风机与防护门距离大于10.9D1时，辅助坑道及正洞内风速流线如图11 所示。由图可知：在这一距离下，单车道辅助坑道内风速分布较为均匀，说明射流风机安装位置较为合理。

为了便于分析，将各工况下，防护门处平均风速计算结果与风机安装位置间的关系绘制成曲线，如图12 所示。由图可知：在单车道辅助坑道内，当射流风机与防护门距离小于10.9D1时，随着距离的增大，防护门处平均风速逐渐增大；当射流风机与防护门距离大于10.9D1以后，防护门处平均风速基本稳定。

当射流风机与防护门距离发生变化时，计算单车道辅助坑道内断面平均风速随风机安装位置的变化规律，结果如图13 所示。由图可知：当射流风机与防护门距离小于10.9D1时，随着距离的增大，单车道辅助坑道内断面平均风速逐渐增大；当射流风机与防护门距离大于10.9D1以后，辅助坑道内断面平均风速基本稳定在1.1 m·s-1。

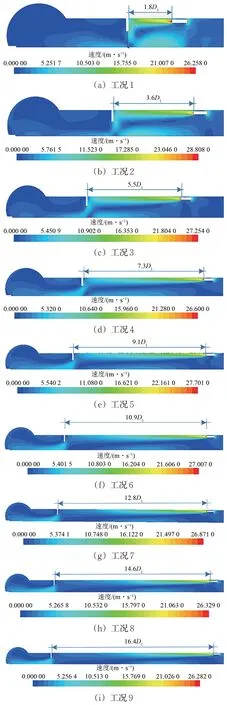
图10 单车道辅助坑道内不同工况下的风速场云图

图11 射流风机与防护门距离10.9D1时单车道辅助坑道及正洞内风速流线图

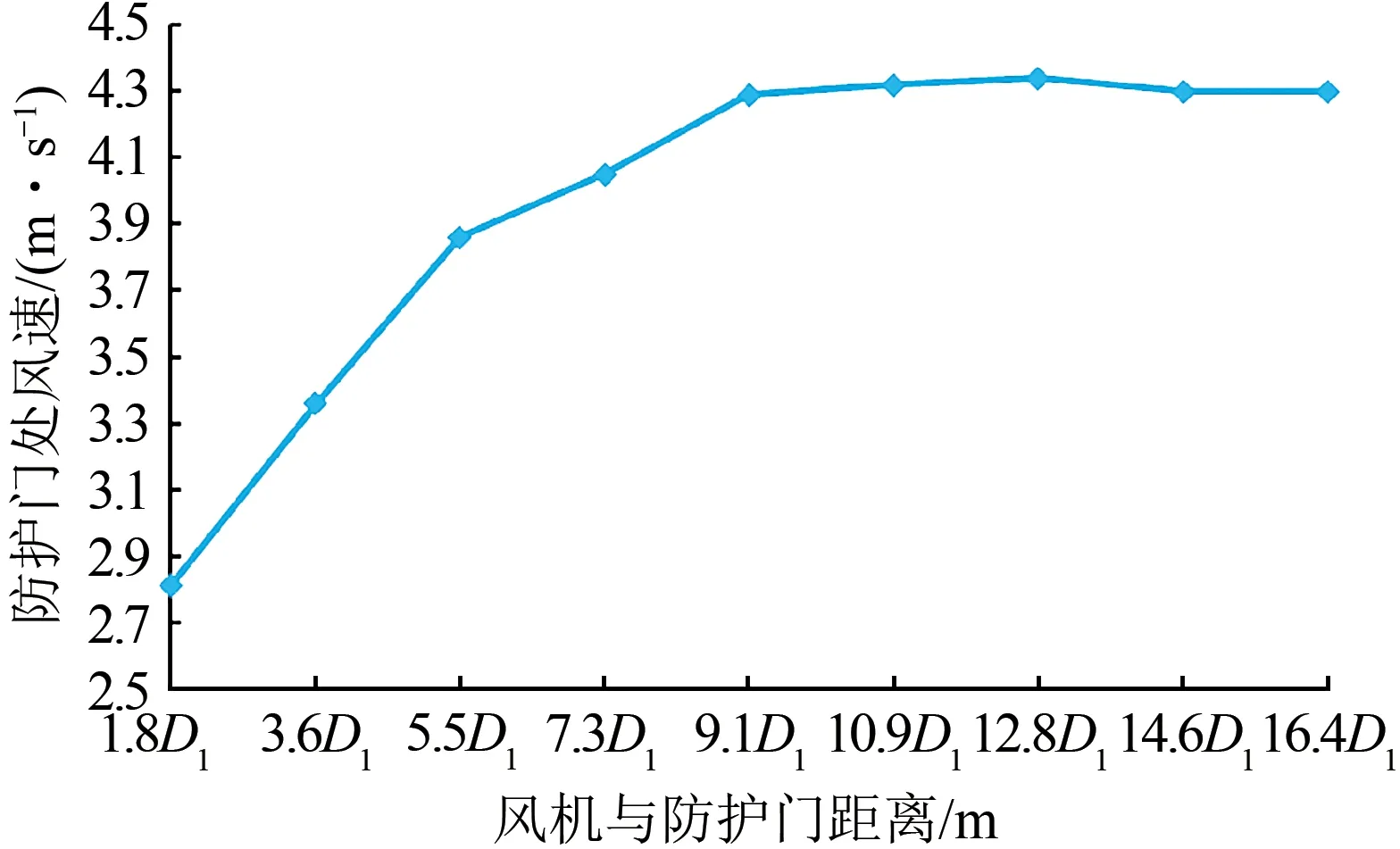
图12 单车道辅助坑道内防护门处风速随射流风机与防护门之间距离变化曲线

图13 单车道辅助坑道内风速随射流风机与防护门之间距离变化曲线

综上，单车道辅助坑道内的射流风机安装位置与防护门之间距离宜大于10.9 倍辅助坑道断面当量直径。

4.3.2 双车道辅助坑道射流风机安装位置

当射流风机安装在双车道辅助坑道断面时，同样需要确定射流风机的最佳安装位置。同样绘制各工况下的辅助坑道内风速云图，如图14 所示。由图可知：当射流风机与防护门距离在1.5D2～4.4D2之间时，射流风机与防护门之间的空间内存在明显回流风场，说明射流损失较大；当风机与防护门距离大于7.4D2时，射流段充分发展，回旋段消失，风流穿过防护门截面时造成的局部损失达到最小值。

图14 双车道辅助坑道内不同工况下的风速场云图

当风机与防护门距离大于7.4D2时，辅助坑道及正洞内风速流线如图15 所示。由图可知：在这一距离下，双车道辅助坑道内风速分布较为均匀，说明射流风机安装位置较为合理。

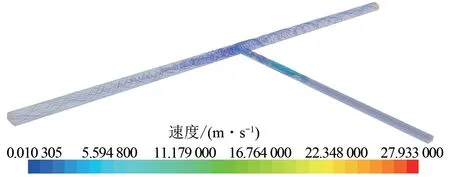
图15 射流风机与防护门距离7.4D2时双车道辅助坑道及正洞内风速流线

为了便于分析，将各工况下，防护门处平均风速计算结果与风机安装位置的关系绘制成曲线图，如图16 所示。由图可知：在双车道辅助坑道内，当射流风机与防护门距离为1.5D2时，防护门处风速为-1.82 m·s-1，即防护门处风流由正洞吹向横洞，此时风向不满足规范要求；当射流风机与防护门的距离由3.0D2增加到13.3D2的过程中，风速由横洞吹向正洞，且随着距离的逐渐增大，防护门处风速逐渐增加；当射流风机与防护门距离增大至7.4D2时，防护门处风速基本稳定于3.28 m·s-1，之后防护门处风速基本不再随风机与防护门之间距离变化。

图16 双车道辅助坑道防护门处风速随射流风机与防护门之间距离变化曲线

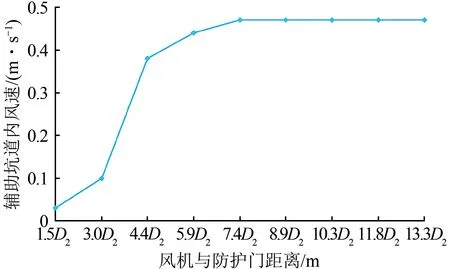
图17 双车道辅助坑道内风速随射流风机与防护门之间距离变化曲线

当射流风机与防护门距离变化时，计算双车道辅助坑道内断面平均风速随风机安装位置的变化规律，结果如图17 所示。由图可知：当射流风机与防护门距离小于7.4D2时，随着距离的增大，双车道辅助坑道内断面平均风速逐渐增大；当射流风机与防护门距离大于7.4D2以后，辅助坑道内断面平均风速基本稳定在0.47 m·s-1。

4.3.3 隧道口救援站平导内射流风机安装位置

为便于分析隧道口救援站范围内整体风速分布情况，取距离隧道轨面以上1.765 m（即模型中Z=1.765 m）平面作为研究断面，该断面在隧道口救援站数值模型中的具体位置如图18 所示。当风机位于不同位置时，绘制各工况下该断面处的风速云图，如图19所示。

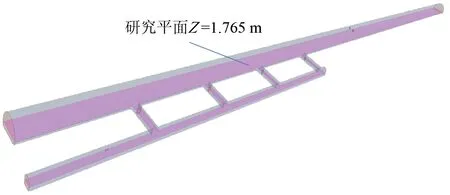
图18 隧道口救援站模型风速研究截面位置

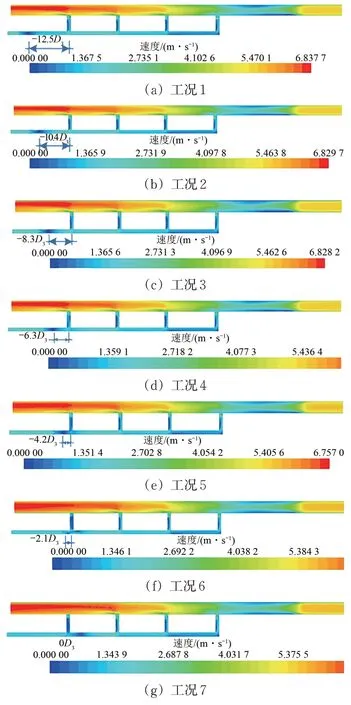
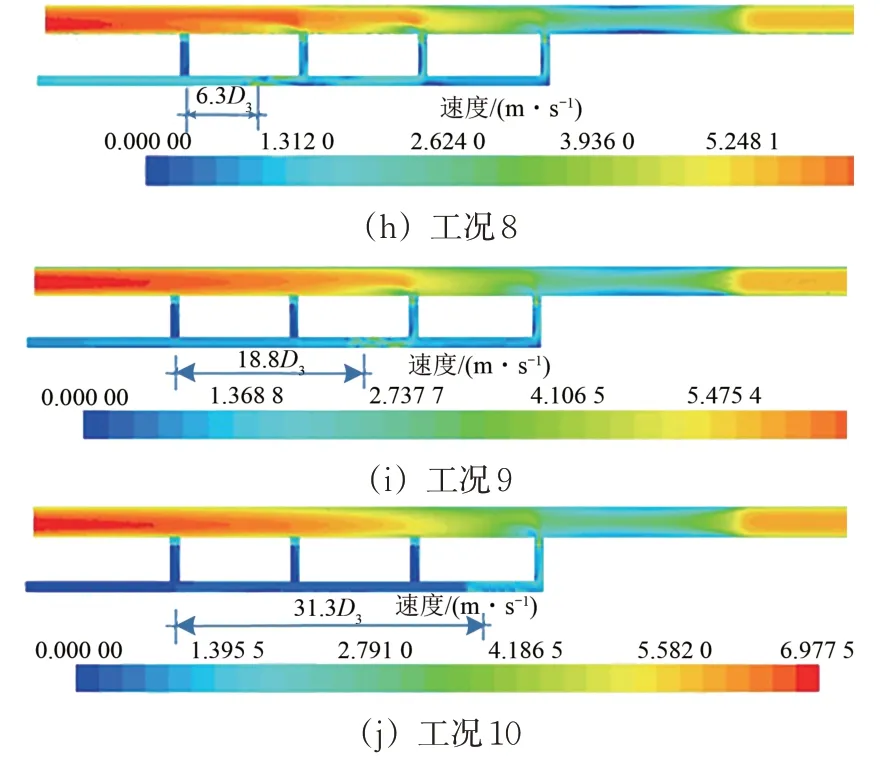
图19 隧道口救援站内射流风机与1#横通道之间距离不同时风速云图

由图19 可知：当射流风机与1#横通道距离由-12.5D3变化至0 时，1#防护门处风速逐渐减小，其余防护门处风速逐渐增大；当射流风机与1#横通道距离由0 变化至31.3D3时，位于射流风机后侧的防护门处风速大幅降低，进而导致防灾通风效果明显变差。

选取射流风机与1#横通道距离为-8.3D3时的情况进一步分析，此时隧道内风速流线如图20 所示。由图可知：各防护门处的风速存在一定差异，靠近平导内侧风机的防护门处风速较大，而远离平导内风机侧防护门风速较小。因此这种通风模式下，最里侧的防护门处风速可作为选择风机配置的参考标准。

图20 射流风机距离1#横通道-8.3D3时隧道内风速流线图

当射流风机安装位置与1#横通道之间的距离发生变化时，整理各防护门处的风速数据，结果如图21 所示。由图可知：在隧道口救援站平导内，当射流风机安装于救援站1#横通道左侧时，2#、3#、4#防护门处风速基本不受射流风机位置影响，1#防护门处风速随射流风机与1#横通道之间距离的减小而减小，即射流风机与1#横通道之间距离越小，通风效果越差；当射流风机与1#横通道距离由-12.5D3变化至-8.3D3时，1#防护门处风速由4.2 m·s-1下降至4.05 m·s-1，下降幅度为3.6%，该区段内风速下降并不明显，1#防护门处风速受射流风机与1#横通道之间距离影响轻微，因此风机安装于该区段较为合理；当射流风机与1#横通道距离由-8.3D3变化至0 时，1#防护门处风速下降幅度逐渐增加，风速由4.05 m·s-1下降至1.43 m·s-1，下降幅度为64.7%，因此该区段为风机安装不合理区段；在射流风机与1#横通道距离由0 增加至31.3D3的过程中，1#防护门处风速持续降低，距离为31.3D3时1#防护门处风速为0.98 m·s-1，因此射流风机不能安装于1#横通道右侧。

图21 防护门处风速随风机与1#横通道之间距离变化曲线

综上所述，隧道口救援站平导内风机应安装于靠近平导出口1侧，当射流风机与最近横通道之间距离大于8.3D3时，各防护门处风速基本稳定，且通风效率较高。

5 结 论

（1）当长大铁路隧道采用射流风机进行防灾通风时，由于辅助坑道与隧道正洞之间存在防护门，射流风机与防护门之间的距离会直接影响其通风效率。

（2）射流风机安装于单车道辅助坑道断面条件下，当射流风机与防护门距离大于10.9 倍辅助坑道断面当量直径时，防护门处平均风速及辅助坑道内的风速基本稳定，建议射流风机安装位置与防护门之间距离宜大于10.9倍辅助坑道断面当量直径。

（3）射流风机安装于双车道辅助坑道断面条件下，当射流风机与防护门距离大于7.4 倍辅助坑道断面当量直径时，防护门处平均风速及辅助坑道内的风速基本稳定，建议射流风机安装位置与防护门之间距离宜大于7.4倍辅助坑道断面当量直径。

（4）当射流风机安装于隧道口救援站平导时，射流风机应安装于靠近平导出口1侧，并且与最近横通道之间距离宜大于8.3 倍平行导洞断面当量直径。