具有未建模动态和输入饱和约束的纯反馈非线性系统自适应神经网络控制

胡汇源,毛 骏

(中国计量大学 机电工程学院,浙江 杭州 310018)

众所周知,在过去的几十年里,非线性系统的稳定性分析和控制器设计一直是一个活跃的问题,文献[1,2]中给出了许多有趣的结果。在这一领域中已经得到了很多有效的控制方法,包括自适应反步法、容错控制以及模糊控制。其中自适应反步法控制的主要特点是它可以在处理非线性系统的控制问题时,无需考虑匹配条件。

在实际工业生产中,由于安全需求或物理限制等因素,系统不能传输无限大的控制信号,因而大部分物理系统都会出现输入饱和约束的情况。例如在航空器控制中,输入饱和约束可能会导致控制器输入输出不一致的“上卷”现象[3];一般的流量执行器存在物理限制,使用中不会使流量趋于无限大[4]。当系统发生饱和时,系统性能将显著下降。因此研究具有输入饱和约束的非线性系统的控制器设计具有实用和理论价值。文献[5]使用模型预测控制方法来处理约束非线性系统。文献[6]中设计抗饱和补偿器用于适应系统中的约束。文献[7]研究了具有输入饱和约束的非线性系统的鲁棒自适应控制。文献[8]利用扩展状态观测器处理了混沌系统的输入饱和约束问题。文献[9]针对具有输入非线性的非线性系统提出了一种自适应变结构控制方法。随着智能控制的发展,文献[10]引入了模糊控制方法来补偿系统中的饱和。文献[11]针对输入饱和约束且部分状态不可测的随机非线性系统提出了构造一个与系统相同阶次的辅助系统。文献[12]采用微分中值定理来应对多输入多输出系统中的输入饱和约束。文献[13]采用了饱和度指示函数分析了非线性严格反馈系统中输入饱和约束的影响。文献[14]采用复合抗干扰控制技术研究了具有不确定性和输入饱和约束的非线性系统的干扰抑制问题。

此外,由于测量噪声、建模误差、建模简化等,未建模动态和动态干扰经常出现在实际系统中,它们是所考虑系统不稳定的来源。例如在对实际系统建模时,常常出现一些无法使用数学模型来进行描述的模型误差,此外有时会对系统进行降阶处理,使得系统的部分动态特性丢失[15]。文献[16]通过将控制器重新设计对含有未建模动态的非线性系统进行控制。文献[17]采用了自适应网络模糊推理系统对非线性系统中的未建模动态进行估计和补偿。文献[18]采用辅助系统处理具有未建模动态的多输入多输出非线性系统。文献[19]通过构造合适的Lyapunov函数处理不确定非线性系统的未建模动态影响。文献[20]采用动态信号处理一类切换非线性系统的未建模动态影响。文献[21]通过雅克比线性化分解将非线性系统中的未建模动态分解为线性项和高阶未知项。

鉴于大量实际工业系统需要依赖纯反馈非线性系统进行建模表征,例如机械系统,飞行器系统等,且实际系统在运行过程中会不可避免地受到输入饱和约束与未建模动态影响,从而使系统性能下降甚至导致系统无法运行,因此研究系统的此类问题具有深远的价值。在控制器设计过程中,引入动态信号处理未建模动态,采用中值定理处理输入饱和约束问题,采用RBF神经网络逼近未知非线性函数,然后通过Backstepping方法系统地推导出自适应神经网络控制方案。本文的主要贡献如下:1) 利用微分中值定理处理系统的输入饱和约束,即对其进行线性化处理,以便设计自适应控制器;2) 利用动态信号处理系统未建模动态;3) 通过估计神经网络基函数权向量的范数,自适应参数的数目不超过所考虑的非线性的阶数,使得计算量大大减少。

1 问题描述与预备知识

1.1 系统描述与基本假设

考虑如下一类具有未建模动态和输入饱和约束的纯反馈非线性系统:

(1)

(2)

其中:v(t)为所需构建的控制律,uM为未知常数。由文献[22]可知,饱和函数可以用如下的光滑函数进行逼近:

(3)

由此饱和函数可以表示为

sat(v)=h(v)+ρ(v)。

(4)

其中ρ(v)为有界函数,它满足

(5)

根据中值定理,h(v)可以表示为

(6)

其中,vθ0=θ0v+(1-θ0)v*,0<θ0<1。选取v*=0,则(6)式可以转化为

(7)

其中,00,h1>0为常数。

此外,再次利用中值定理,可得

(8)

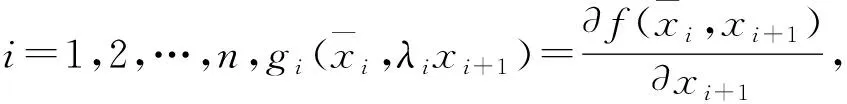
注1:需要指出的是,纯反馈非线性系统是一种结构较为普通的非线性系统,并且许多实际工业系统需要依赖纯反馈非线性系统进行建模以表征系统动态,例如机械系统,飞行器系统等。

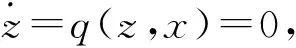
现针对本文给出如下假设:

假设1:未知动态扰动Δi(i=1,…,n)满足如下条件:

(9)

其中:φi1,φi2为未知非负光滑函数。

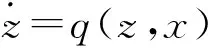
(10)

其中,α1(·),α2(·)和μ(·)是K∞类函数,且c0>0和d0>0为已知常数。

(11)

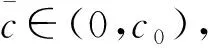
(12)

使得当t≥T0时,有D(t)=0,当t≥0时,有

V(z(t))≤r(t)+D(t)。

(13)

(14)

其中:μ0(·)为非负光滑函数。

引理2[26]:如果满足x∈Rn,y∈Rn,p>1,q>1并且p-1+q-1=1,则可以得到

(15)

其中:ε>0为任意常数。

特别地,若p=q=2,则有

(16)

1.2 神经网络逼近理论

神经网络是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。这种网络通过调整内部大量节点之间相互连接的关系达到处理信息的目的。RBF神经网络拓扑结构图如图1[27]。其中,RBF神经网络由输入层,隐含层和输出层3层组成。

图1 RBF神经网络拓扑结构Figure 1 Topology structure of RBF neural networks

对于任意给定的未知非线性光滑函数f(X):Rq→R,在紧集ΩX上采用RBF神经网络对其进行逼近可得

f(X)=φ*Tξ(X)+δ(X),∀X∈ΩX。

(17)

其中,X∈ΩX∈Rq为神经网络的输入向量,δ(X)为逼近误差,其满足|δ(X)|≤ε,ε>0是未知的常数。l为神经网络节点数目,且l>1,ξ(X)=[ξ1(X),ξ2(X),…,ξl(X)]T∈Rl是已知的光滑向量函数,基函数ξi(X)通常选取如下高斯函数:

(18)

其中,μi=[μi1,μi2,…,μiq]T,ηi分别表示高斯函数的中心和宽度。理想权向量φ*=[φ1,φ2,…,φl]T定义为

(19)

控制目标:针对式(1)系统设计状态反馈控制律实现实用镇定。

2 控制器设计

本节将对自适应控制律进行设计,设计过程共分为n步,设计过程将基于如下的坐标变换:

zi=xi-αi-1,i=1,2,…,n。

(20)

其中,α0=0,且αi(i=1,2,…,n-1)为第i步所需设计的虚拟控制律,控制律u将会在第n步中给出。

第1步:选取如下的Lyapunov函数:

(21)

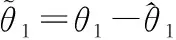
(22)

基于如下关系式:

(23)

其中ε>0为任意常数,由此,可得

(24)

进一步,根据式(23)以及引理2,可得

(25)

将(24)式和(25)式代入到(22)式,可得

(26)

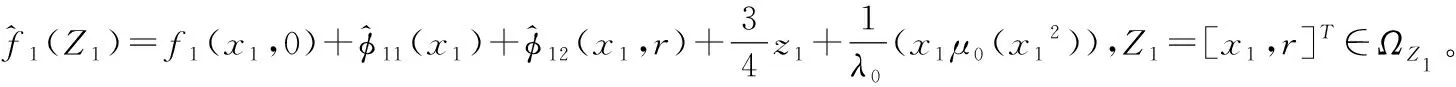
(27)

其中,δ1(Z1)是估计误差,ε13>0为常数。

将(27)式代入(26)式,可得:

(28)

依据引理3,可知

(29)

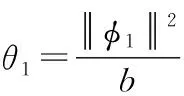
将(29)式代入(28)式,可得

(30)

构造如下虚拟控制律:

(31)

其中,k1>0,σ1>0和η1>0为设计参数。

将(31)式代入(30)式,依据假设3和引理2,可得

(32)

第i步(2≤i≤n-1):选取如下的Lyapunov函数:

(33)

其中γi为设计参数。

基于坐标变换zi=xi-αi-1,可得

(34)

根据已得到的虚拟控制律及系统(1),可得

(35)

根据假设1和(23)式,可得:

(36)

(37)

(38)

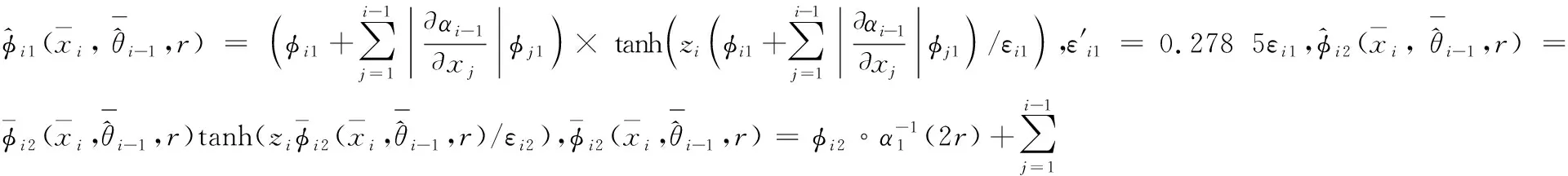
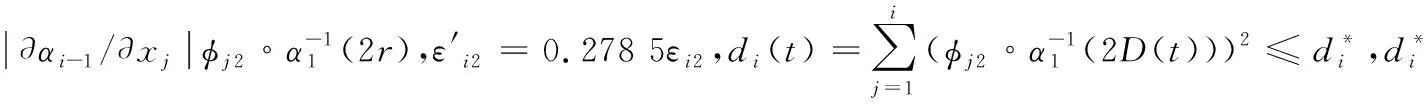
将式(36)～(38)代入到式(35),可得

(39)

(40)

其中,δi(Zi)是估计误差,εi3>0为常数。

根据引理2,可得

(41)

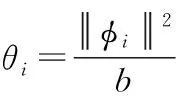
构造如下虚拟控制律:

(42)

其中ki>0,σi>0和ηi>0为设计参数。

将式(40)～(42)代入到式(39)中,可得

(43)

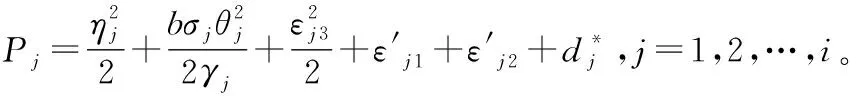
第n步:选取如下的Lyapunov函数:

(44)

其中γn为设计参数。

基于坐标变换zn=xn-αn-1,可得

(45)

根据已得到的虚拟控制律及式(1)系统,可得

(46)

根据假设1和(23)式,可得

(47)

将式(47)代入到式(46)中,可得

(48)

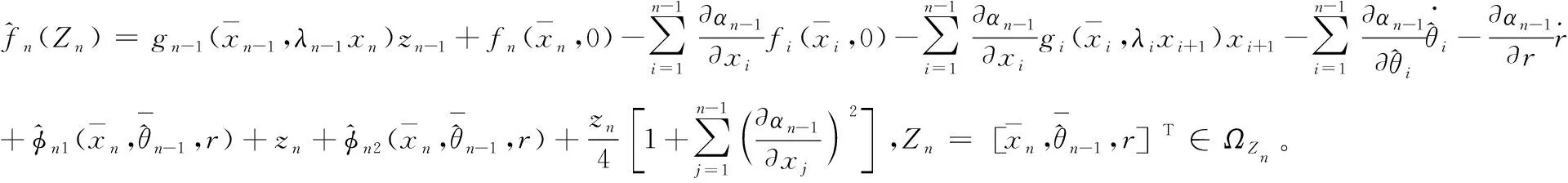
(49)

其中,δn(Zn)是估计误差,εn3>0为常数。根据引理2,可得

(50)

将式(50)和式(49)代入到式(48),可得

(51)

根据引理2和假设3,可得

(52)

其中

(53)

将式(52)代入到式(51)中,可得

(54)

设计系统控制律为:

(55)

其中,kn>0,ηn>0,γn>0,σn>0为设计参数。

将式(55)代入到式(54),可得

(56)

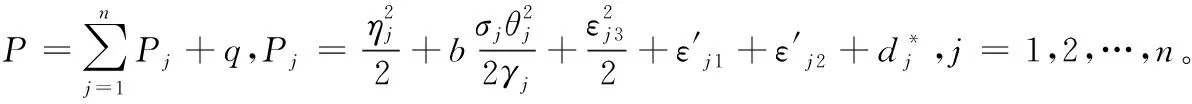
3 稳定性分析

定理1:考虑具有输入饱和约束与未建模动态的纯反馈非线性系统(1),若其满足假设1～3,在合理的参数作用条件下,则可利用自适应控制律(55)实现该闭环系统的实用渐近稳定,且闭环系统所有信号一致终结有界。

证明:选取Lyapunov函数V=Vn,可得

(57)

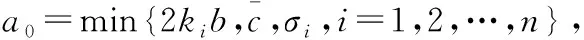
对(57)式求解,可知其满足

(58)

即

(59)

综上所述,为了便于工程应用,本文现总结如下控制算法。

控制算法第1步:选取控制参数k1>0,σ1>0,η1>0以及γ1>0以构建(31)式所示的虚拟控制律α1以及参数自适应控制律。第2步:利用坐标变换(20)式以及前述虚拟控制器α1获取信号z2,并选取控制参数k2>0,σ2>0,η2>0以及γ2>0构建控制律α2以及参数自适应控制律。第3步:利用虚拟控制律αi(i=2,…,n-1)重复迭代坐标变换(20)式,并选取控制参数ki>0,σi>0,ηi>0以及γi>0(i=3,…,n)构建(42)式所示的虚拟控制器αi(i=3,…,n-1)以及参数自适应控制律,由此导出(55)式所示的控制律v以镇定非线性系统(1)。

此外,本文的控制流程图如图2。

图2 控制流程图Figure 2 Control flow chart

4 系统仿真

为了验证设计的可行性,考虑对满足式(1)系统条件的如下系统进行仿真验证:

(60)

其中:饱和输入u为:

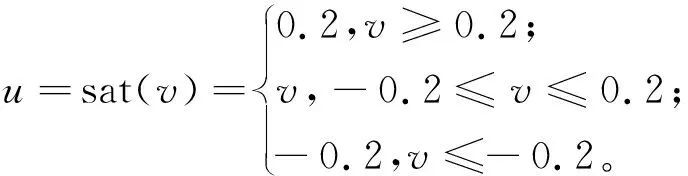
(61)

(62)

图3 x1(实线),x2(点划线)和x3(虚线)的轨迹Figure 3 Trajectories of x1 (full line), x2 (dash-dotted line) and x3 (dotted line)

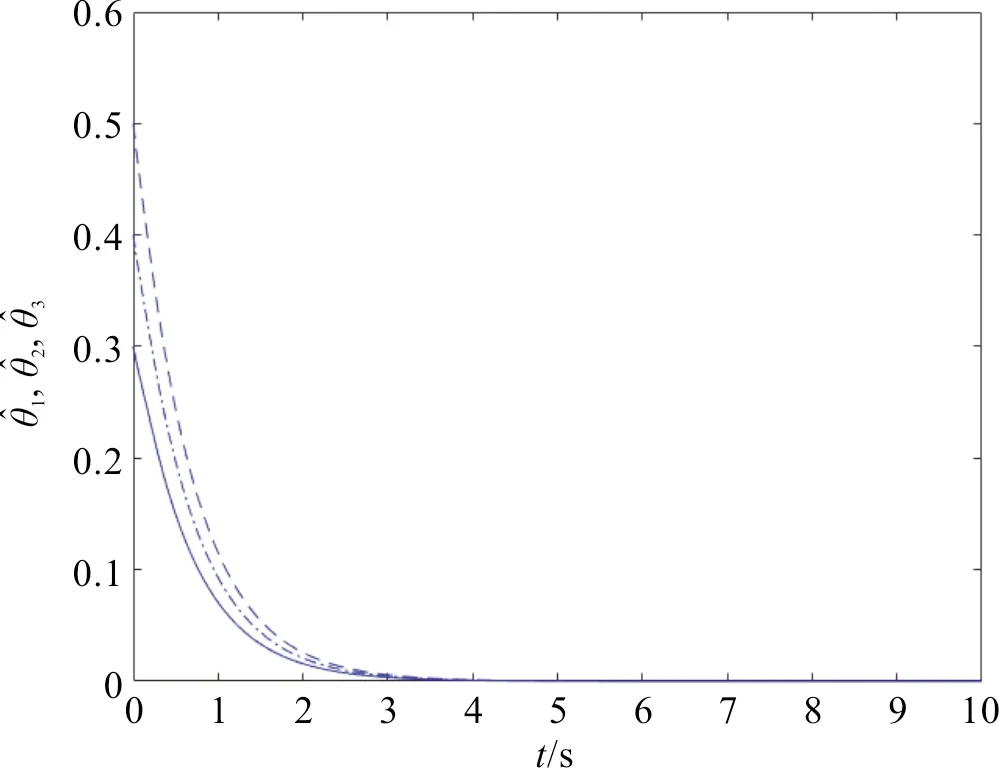
图4 实线(点划线)和(虚线)的轨迹Figure 4 Trajectories of (dash-dotted line)

图5 未建模动态zFigure 5 Trajectory of the unmodeled dynamics z

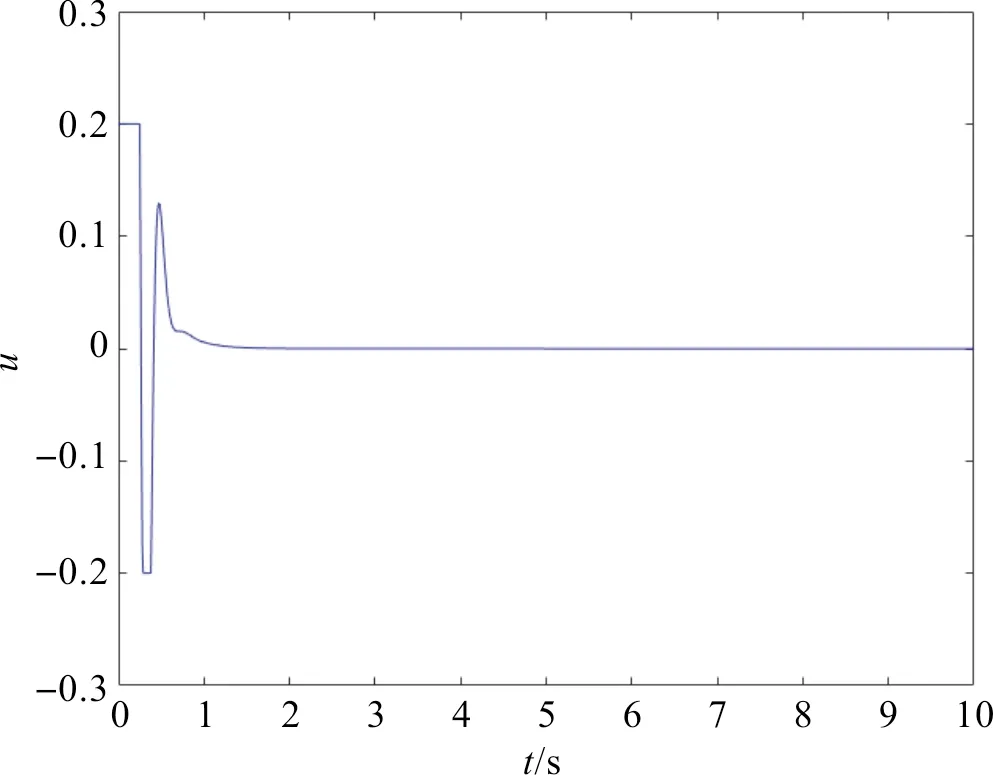
图6 控制信号uFigure 6 Control input u

5 结 论

本文对于一类具有输入饱和约束与未建模动态的纯反馈非线性系统,基于Backstepping方法设计了一种自适应神经网络控制方案,该方案通过引入动态信号处理系统的未建模动态,并采用中值定理处理输入饱和约束问题。通过选取合理的Lyapunov函数证明了闭环系统中所有信号均为半全局一致终结有界。