复质心体的性质
金 天, 冷岗松
(上海大学理学院, 上海 200444)
Busemann-Petty 质心体不等式是一个非常重要的仿射等周不等式[1-2], 其应用正被广泛研究[3-5].下面给出Busemann-Petty 质心体不等式研究的质心体的定义.
给定一个内部非空的凸体K ⊂Rn,它的质心体ΓK的支撑函数为[6]

式中: 积分是关于Lebesgue 测度;“·” 表示标准的欧氏内积;u、x表示变量.
令K0(Cn)表示包含原点在内部的复凸体所构成的集合, 下面给出质心体的定义.
定义1[7]关于K ∈K0(Cn)的复质心体ΓCK的支撑函数定义为

式中: 积分是关于Lebesgue 测度在关于R2n和Cn标准同胚下的拉回;Cu:={cu:c ∈C},C为复平面上的凸体.注意到|u·x|=h[−1,1]u(x),这说明了复质心体是经典质心体的推广.
1 预备知识
Rn表示n维欧氏空间,Kn是Rn中凸体(非空紧凸集)的集合.表示Rn中所有原点在内部的凸体的集合.Cn表示n维复空间,K(Cn)定义为Cn中所有凸体的集合,K0(Cn)定义为Cn中所有原点在内部的凸体的集合.复凸体K的体积记为|K|[8].
若K ∈Kn, u ∈Sn−1,则凸体K的支撑函数为[9]

并记h(K,u)=hK(u).
若ιK是R2n中的一个凸体,那么集合K ⊂Cn可以被称为一个复凸体.记ι: Cn →R2n为标准同构[6,10-11], 即有

式中:R、S分别是实部和虚部.不难验证
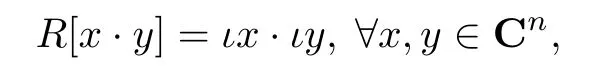
式中: “·”表示R2n中的标准欧氏内积.
下面给出复凸体的支撑函数.
一个凸体K是被它的支撑函数hK:Cn →R 唯一确定的, 即有

对于一个复数c ∈C,记为其共轭,|c|为其模长.用“·”表示Cn内积, 即x·y=x ∗y,∀x,y ∈Cn.B表示{c ∈Cn:c·c≤1}的单位球,Sn表示单位球面{c ∈Cn:c·c=1}.
对∀K,L ∈K(Cn), α,β≥0(α、β不同时等于0),则其Minkowski 线性组合为[8]
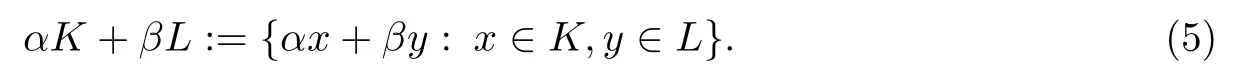
式(5)等价于

根据复凸体支撑函数的定义,对于K,L ∈K(Cn),显然有

由上可知, 一个凸体与其支撑函数是一一对应的.
2 性 质
下面研究复质心体的基本性质,探究复质心体在复平面上是否满足线性性, 以及凸体和的复质心体与复质心体和的某种包含关系, 并进一步推广到若干个凸体的情况.
定理1对λ1,λ2>0,若K ∈K0(Cn), C1,C2∈K(C),则有
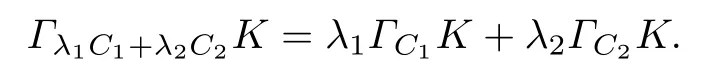
证明 根据式(2)可知,ΓC1+C2K的支撑函数为

结合式(5)和(6), 由支撑函数的线性性可得
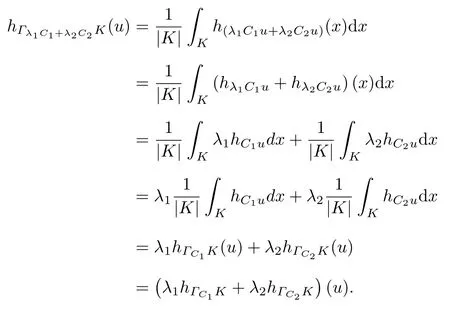
因为凸体与其支撑函数是一一对应的,故有
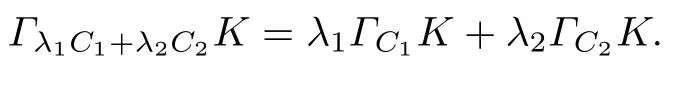
因此,ΓCK的线性性得证.
定理2对λ≥0,若C ∈K(C),K ∈K0(Cn), 则有

证明 根据式(2)可以写出ΓC(λK)的支撑函数,并结合式(5)和(6)有

故有
故定理2 得证.
定理3对K,L ∈K0(Cn),C ∈K(C),则有
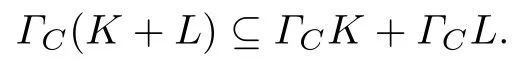
证明 根据复质心体支撑函数的定义, 可得
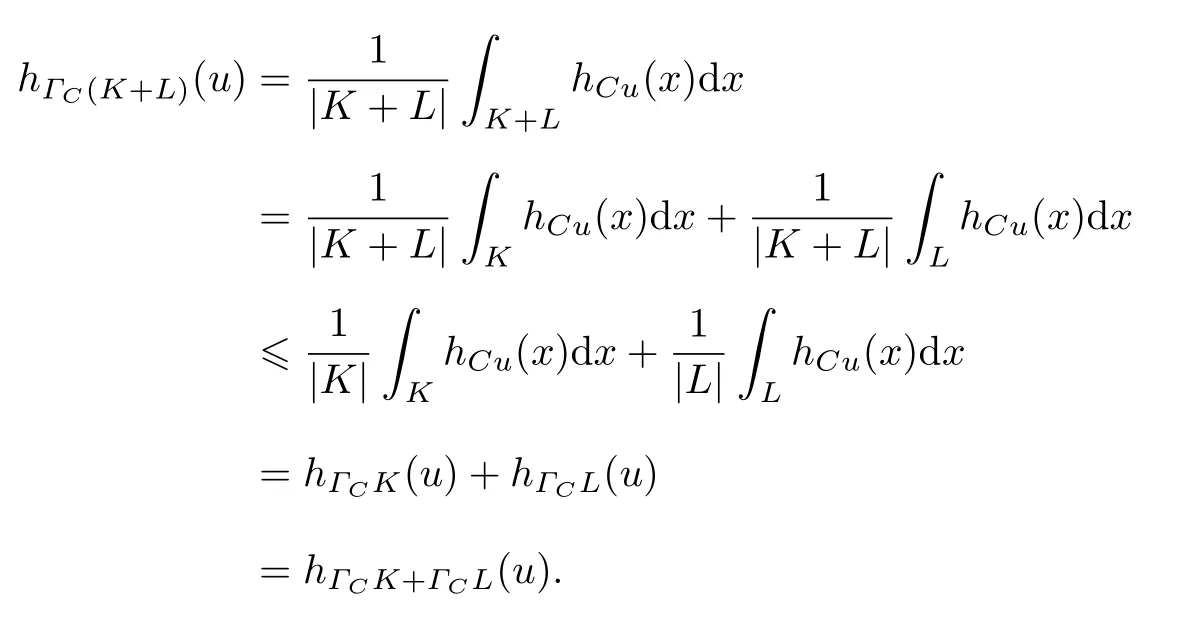
故有

故定理3 得证.
显然根据上面的研究, 可以推广到n个凸体的情况.
推论1令C ∈K(C),K1,K2,··· ,Kn ∈K0(Cn),则有
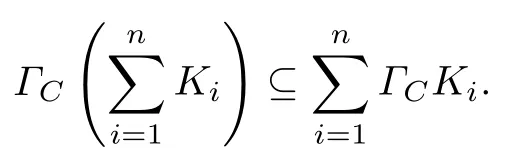
证明略.

