具有常平均曲率的曲率子流形上一类 Schrödinger 算子的特征值估计

杜玮翎

(湖北大学数学与统计学学院，湖北 武汉 430062)

0 引言

子流形作为微分几何的一个重要分支，内容十分丰富.常平均曲率子流形是子流形中重要的一类，有许多有意义的结论，特别是对极小子流形的研究，得到了许多重要定理.如著名的Simons不等式[1]，

即：设Mn是单位球面Sn+p(1)的n维紧致无边的极小子流形，S表示其第二基本形式模长的平方，则有

其中*1表示M上的体积元.Simons不等式给出后，陈省身[2]，李安民[3]等又继续得出了一些推论.

最近，Chen-Cheng[5]利用Jacobi算子的特征值，刻画了球面上的常平均曲率的超曲面，对超曲面进行了分类.

事实上，若将单位球面Sn(1)看作是欧氏空间Rn+1的超曲面，则球面中的任意子流形均为曲率子流形，因此研究具有常平均曲率的曲率子流形是自然且有意义的.Wu[6]研究了曲率子流形的基本方程，张宇萍[7]证明了极小曲率子流形的一个Simons型不等式的结论，推广了Simons的结论.基于以上研究，本文中利用一类Schrödinger算子的特征值，继续研究了曲率子流形的一些性质，推广了Wu[4]、Chen-Cheng[5]的部分结论.

1 预备知识

1≤A,B,C,…≤n+p;1≤i,j,k,…≤n;n+1≤α,β,γ,…≤n+p.

令{ωA}是{eA}的对偶标架场,当限制在Mn上时,有ωα=0，则有0=dωα.

由Cartan引理可知

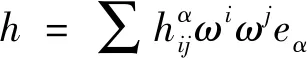
(1)

(2)

可得Ricci恒等式

(3)

(4)

(5)

(6)

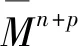
其中*1表示Mn的体积元.

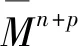
(7)

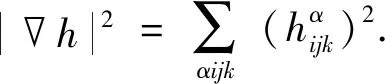
当且仅当bi中至少有n-1个相等时等号成立.

2 主要定理及证明

(8)

这里*1表示M的体积元.

定理2.1的证明如所知

当地种植的大田作物主要有水稻、玉米、小麦等。当前除了冬小麦播种有少量用肥需求，当地已经基本进入用肥淡季。受化肥价格持续高位影响，加上农产品的价格低，当地农民用肥量有所减少，尤其在施肥结构方面，因尿素的价格大大高于往年同期，所以很多农民尿素的使用量大大降低，相应地，复合肥的使用量有所增加。

(9)

由于M是非全测地的，则

通过直接计算可知

由引理1.2，我们有

由文献[6]，可得

于是

因而

(10)

由(9)式和(10)式，我们得到

令ε→0，结合|λ|≥c(c>0).

2)μ1=0，当且仅当S=0.

2)若S=0，显然算子L1=-Δ，μ1=0.反之，若μ1=0，则由定理2.1可知M必是全测地的.

结合定理2.1和定理2.2，我们得到：

1)μ1=0，如果Mn是全测地的.

2)μ1≤-nc2，其他.

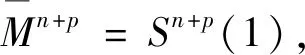
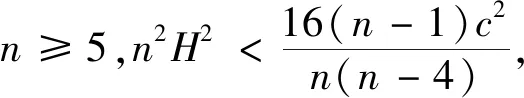
下面，我们假设H≠0，由(9)～(10)式可得

(11)

令μi=κi-H，则有

(12)

(13)

由(11)～(13)式可得

(14)

对任意常数α>0，ε>0，令fε=(B+ε)α，则由(14)式计算得到

(15)

又由于H是常数，则

因此

又对任意常数β,可得

(16)

又因为

于是

=0

(17)

由(16)、(17)式，可得

当1-2α(1-β)>0时，

因为M是非全脐曲率子流形，则

令ε→0，结合|λ|≥c>0.

则有

(18)

λ1≤-nH2-n(c2+H2).

又由

可知

(19)

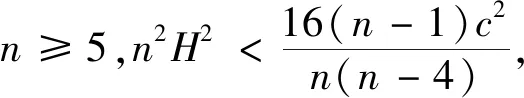
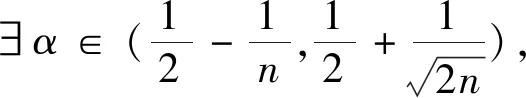
则此时

(20)

代入(18)式知

(21)

结合(20)式，计算可得

4(n-1)(1-2α(1-β))(c2+H2)-2α(1-β)(n-2)2H2

(22)

由 (18)、(21)、(22)式，可得

(23)

定理得证.

3 结束语

本文中研究了具有常平均曲率的曲率子流形上的一类Schrödinger算子，估算了其第一特征值的上界，推广了Wu[4]、Chen-Cheng[5]的部分结果.由于曲率子流形中外围空间的性质不确定，本文中结果未得出刚性的情形，这也是以后可研究的一个方面.同时，根据Chen-Cheng的结果，余维数p≥2情形下的Jacobi算子的特征值估计，带权的Jacobi算子估计等都是可以考虑的问题.