考虑分布轴向力的细长杆横向振动与失稳分析1)

孙秀荣 张立娟 赵洁妤 宋 杨

(河北环境工程学院，河北秦皇岛066102)

欧拉杆柱失稳临界载荷的计算在高校教材《材料力学》中并未考虑杆柱的分布轴向力因素[1]，《机械系统动力学》中梁的横向振动也并未考虑此因素[2]。目前高等教材中杆柱失稳问题，主要集中在欧拉杆柱的临界载荷的计算上[3-6]；涉及梁柱的横向振动，主要集中在欧拉伯努利梁的横向振动的仿真和计算上[7-13]。与此对应，上述计算得到的结论也未涉及到梁柱的分布轴向力的影响。针对几百甚至上千米的超长杆柱，分布轴向力对梁柱的失稳和横向振动的影响问题，至今未看到有效的文献直观地体现在教材的拓展中。在近些年的教学过程中，不少教育工作者面临此方面的困惑，却由于参考文献匮乏而得不到较好的解答。因此，目前对欧拉杆失稳、欧拉伯努利梁问题进行延拓是必要的，对工程领域也有较强的指导意义。

作者近几年致力于杆管柱的屈曲失稳和横向振动领域的研究[14-16]，在前期经验积累的基础上，建立了本文分布轴向力下的杆柱失稳和横向振动的力学、数学模型，给出近年来热门的数值计算方法，得出更为切合实际的数值分析结果，同时为高校力学方面的教学研究和工程实际运用提供一些指导。

1 力学模型

不考虑细长杆柱的纵向振动与扭转振动对横向振动和屈曲失稳变形的影响，并做如下假设：细长杆柱为铅垂杆；杆柱质地均匀；杆柱顶端为固定端约束，底端为滑动铰支约束。力学模型如图1 所示。

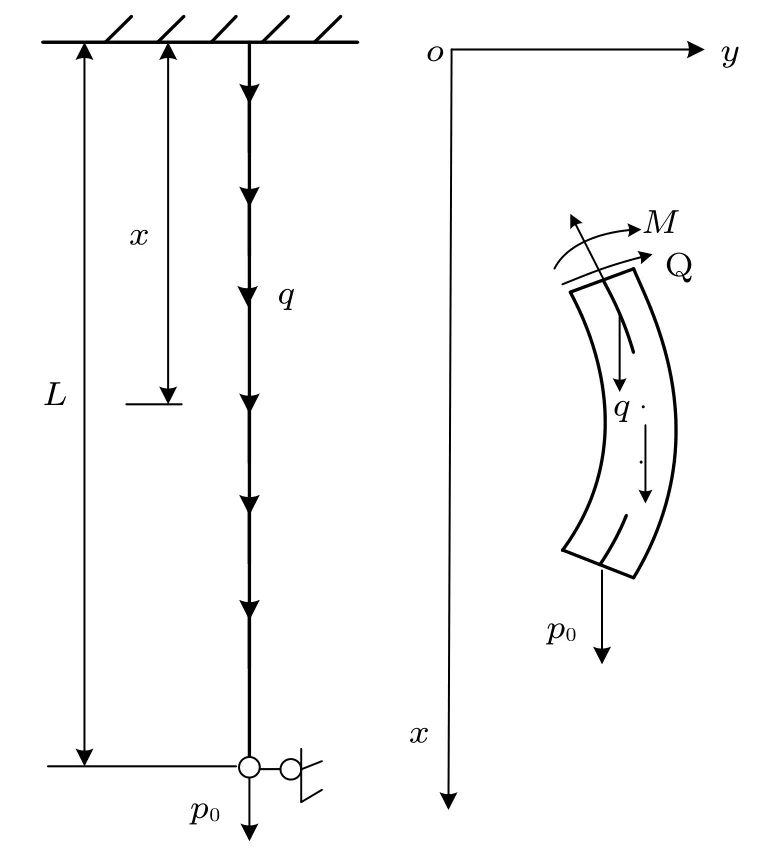
图1 抽油杆柱横向弯曲力学模型

2 分布轴向力下杆柱失稳模型及临界载荷计算方法

根据图1 力学模型，建立细长杆柱的数学模型为

方程(1) 进一步化为

其中

式中，L 为抽油杆柱全长，m；q 为抽油杆柱轴向分布力，N/m；E 为抽油杆柱材料弹性模量，GPa；ε 为抽油杆柱线性分布轴向力比例系数；I 为抽油杆柱的抗弯惯性矩，m4；p0为抽油杆柱端部受力(向下为正，受拉；向上为负，受压)，N。

边界条件为

式(3)即为含有分布轴向力的杆柱屈曲方程，难于求出精确的解析解。

当q =0 时，方程(1) 化为

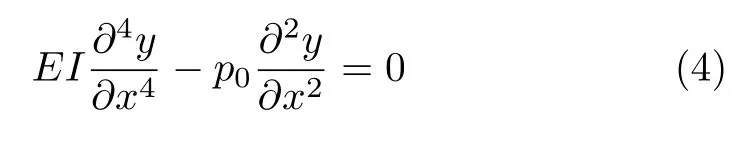
p0为负值时，杆柱受压，式(4)与材料力学中的压杆稳定性方程一致。

2.1 有限差分法求解

将杆柱划分为n 段，得到n+1 个节点。差分格式为

将式(5)～式(7) 代入方程(2) 离散化得

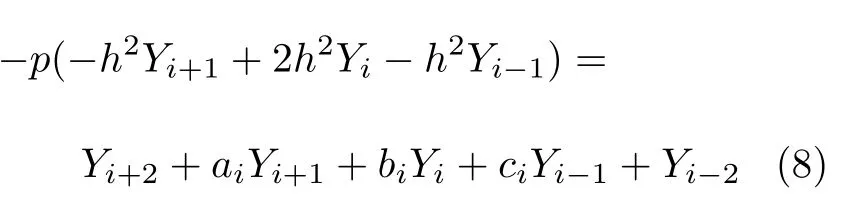
式中，ai= βh3/2-h2(1-X)β -4，bi= 2h2(1-X)β+6，ci=-βh3/2-h2(1-X)β-4。

由边界条件可知

将式(8) 和式(9) 展开成矩阵形式得

即为

式(11)两边同乘A-1，可化简为pY =A-1BY，求出A-1B 的最小特征值，即可求得p，则临界载荷Fcr=-p0=-pEI/L2。

2.2 伽辽金法

设满足边界条件(3) 的形函数为

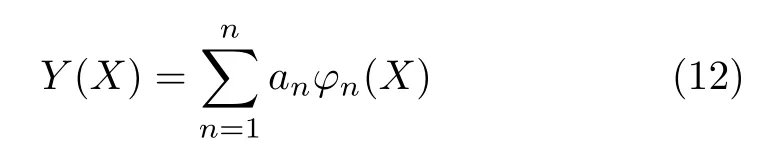
其中

式中，λn= βnL 由超越函数cos λnchλn= 1 确定，λn≈(n+1/4)π。

同理，得到迦辽金方程为整理方程(14)，得到关于一待定系数列阵[an] 的齐次线性方程组

其中，Lnn= (λn)4I1nn- pI2nn- βI3nn，Lmn=(λn)4I1mn-pI2mn-βI3mn+βI4mn。I1nn，I2nn，I3nn，I1mn，I2mn，I3mn，I4mn为积分常数。

an有非零解的条件为

可求得失稳时的临界载荷，将其代入式(16) 可得到振型函数。

3 轴向分布力下的杆柱横向振动数学模型及固有频率计算方法

根据图1 力学模型，建立杆柱的横向振动数学模型为

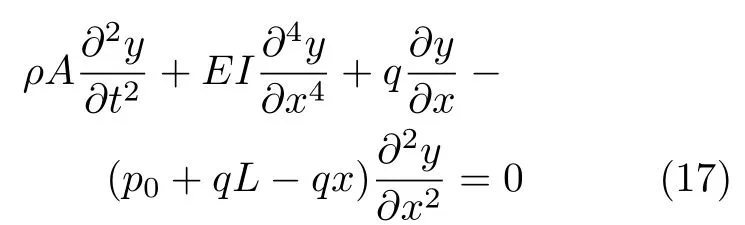
边界条件为

3.1 积分法

先将y(x，t)分离变量，即令y(x，t)=Z(x)F(t)，则方程(17) 可化为

为便于计算，式(19) 中参数进行变换，则

对式(19) 进行四次积分，并整理得

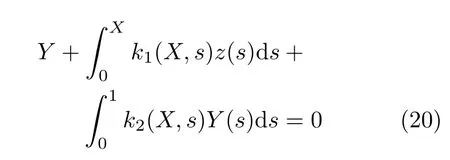
式中

设z(ξ) 为多个多项式之和，采用级数解来逼近其真实解，则

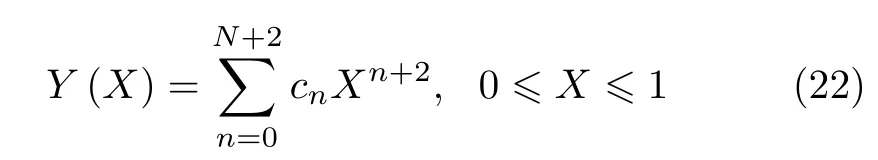
将式(22) 代入式(20) 得

式中

若cn有非零解，则

由式(24) 求解出Ω，即可进一步得到杆柱横向振动固有频率ω。特殊地，当q =0 时，p0=0，方程(17)化为

式(25) 与教材[2] 中梁的横向自由振动方程是相同的，此方程有解析解，亦可采用此方法求解。

3.2 伽辽金法

令

将式(27) 代入方程(17)，得振型方程为

设满足边界条件的形函数为梁自由振动函数

φn(X) 同式(13)。将式(28) 和式(29) 代入式(27)，得到迦辽金方程为

整理方程(30)，得到关于一待定系数列阵[an] 的齐次线性方程组为

其中

I1nn，I2nn，I3nn，I1mn，I2mn，I3mn，I4mn为积分常数。an有非零解的条件是

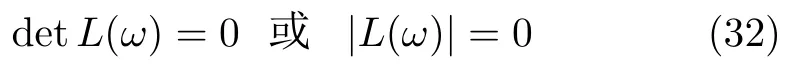
可求得各阶固有频率，将其代入式(32) 可得到振型函数。

4 两种模型数值分析

4.1 杆柱失稳临界载荷

4.1.1 准确性测试

当分布轴向力q = 0 时，数学方程(1) 简化为《材料力学》教材[1]中的模型，而数学方程(17) 简化为《机械系统动力学》教材[2]中的模型。其他参数为L = 5 m，d = 20 mm，E = 209 GPa 时，材料力学欧拉杆临界载荷公式为

采用式(33) 欧拉法、2.1 节差分法、2.2 节伽辽金法分别求解相同参数下杆柱的临界载荷为1322.5 N，1325.7 N，1321.2 N，可知，差分法和伽辽金法的结果与公式(33) 求解结果误差微小(误差在0.25%以内)，说明差分法和伽辽金法求解欧拉杆临界载荷精度较高。

4.1.2 考虑分布轴向力失稳载荷

取基本参数：E =209 GPa，d=20 mm。差分法和伽辽金法得出不同杆长下的杆柱临界载荷规律如图2 和图3 所示。由两图可知，在杆长为50 m 以内时，差分法和伽辽金法得到的临界载荷规律相同，即随杆长的增加而减小；但杆长为50 m 以上时，伽辽金法所得杆柱临界载荷会随杆长的增加而增加，这与差分法所得规律截然相反。由此可知，两种方法在计算考虑分布轴向力较长杆柱的临界载荷时有一种方法得到的结果是不准确且不适用的。而伽辽金方法实质是一种近似计算方法，在杆长超越极限时结果会失真，因而不再适用。这也说明近似方法会有它本身的适用范围，而伽辽金法不适用于考虑分布轴向力且杆长超越一定长度的杆柱的临界载荷的计算。

图2 差分法所得临界载荷变化

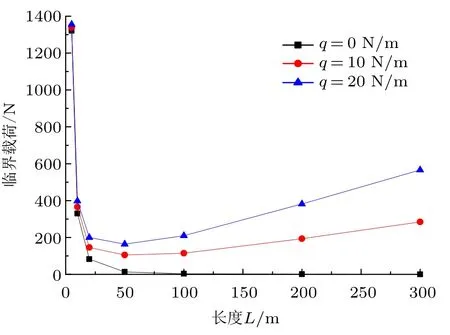
图3 伽辽金法所得临界载荷变化

4.2 杆柱横向振动固有频率和振型

4.2.1 准确性测试

情况一：当基本参数为L = 5 m，d = 20 mm，E = 209 GPa，q = 0 N/m，且底部载荷p0= 0 时，杆柱则做横向自由振动，其固有频率可表示[2]为

采用式(34)、3.1 节积分法和3.2 节伽辽金法求解该相同参数下杆柱的固有频率，其结果对比如表1 所示。由表1 可知，前六阶固有频率所得结果误差很小(0.15%以内)。因此，不考虑端部载荷和分布轴向力时，积分法和伽辽金法求解杆柱横向振动固有频率和振型精度都很高。

表1 未考虑分布轴向力计算固有频率(单位：HZ)

情况二：在情况一参数基础上，只变动p0，令p0=2000 N，得到杆柱横向振动的固有频率，如表2所示。由表2 可得，底端杆柱受拉的情况下，积分法和伽辽金法求解杆柱固有频率时误差甚小(0.02%以内)，说明两种方法均适应于杆柱受拉情况杆柱固有频率计算。

4.2.2 考虑分布轴向力和杆长变化的横向振动

情况三：固有频率随轴向分布力和杆长的变化规律。假设基本参数为d=20 mm，E=209 GPa，p0=500 N，改变轴向分布力q和L，得到杆柱固有频率随分布轴向力q和L的关系曲线，如图4 所示。由图4 可知，固有频率随分布轴向力的增大而增大，而随杆柱长度的增长而减小。q变化范围在0～20 N/m 时，50 m 内杆柱长度固有频率最大误差率为26.96%，100～2000 m 内杆柱长度固有频率最大误差率为390.6%。由此说明，在杆柱长度较短时，分布轴向力对固有频率的影响不大，杆柱较长时，分布轴向力对固有频率影响较大。杆柱较长时，分布轴向力不宜忽略。

图4 固有频率随杆长L 和分布轴向力q 的变化曲线

情况四：固有频率随底端载荷变化的规律。考虑到分布轴向力在杆柱较长时不宜忽略，取基本参数q=20 N/m，L=1000 m，d=25 mm，E=209 GPa，得到不同载荷下杆柱的固有频率变化曲线，如图5 所示(图中p0＞0 为杆柱受拉，反之受压)。由图可知，随着底部受拉载荷的减小，固有频率逐渐下降，底端载荷为0 后继续减小载荷(即反向加载，受压载荷逐渐增大)，受压载荷越过一定值后，固有频率变为虚数。说明在底部载荷逐渐变化的过程中，有一载荷对应着固有频率为0 的情况。令一阶固有频率为0，由2.1 节求得静力学下临界载荷即p0=-169.8 N，失稳变形曲线如图6 所示。由3.1 节求得动力学下横向振动的变形曲线同样如图6 所示。由图可知，两变形几乎完全重合，杆柱失稳时最大变形均出现在杆柱底部附近。说明此时静力学下考虑分布轴向力q=20 N/m 杆柱失稳的变形即为动力学下横向振动变形，而p0则为失稳时的临界载荷。由此可知，考虑分布轴向力的杆柱在非零变形时的固有频率为0，即一阶固有频率为0 时，杆柱达到失稳的必要条件。特殊的，当分布轴向力为0 且杆柱屈曲时，其固有频率对应为0，该结论与文献[8] 一致。

图5 固有频率随底端载荷的变化曲线

图6 杆柱变形规律

图6同时给出了不考虑分布轴向力(即q= 0)时杆柱的静力失稳变形曲线，与q= 20 N/m 时失稳变形曲线对比可知，两者的最大变形位置(即突变处) 明显不同，即杆柱最先达到失稳的位置点不同。不考虑分布轴向力的杆柱最先在靠近中间位置失稳，而考虑分布轴向力的杆柱最先在靠近端部位置处失稳(距离底端约为8.5 m 处)，这也说明了分布轴向力对杆柱最先失稳位置有显著的影响，即超长杆柱计算失稳问题须考虑分布轴向力。

5 工程实例求解

5.1 考虑分布轴向力的螺杆泵杆柱固有频率和振型

数学模型方程(17) 和方程(18) 可应用在求解螺杆泵杆柱的固有频率上，其参数如表3 所示。计算的前五阶固有频率如表4，其对应的振型函数如图7所示。

表3 螺杆泵基本参数表

表4 考虑分布轴向力的固有频率结果(单位：HZ)

由表4 可知，当细长杆柱底端受拉时(p0＞0)，积分法和伽辽金方法得到的固有频率误差很小(0.5%以内)，可以忽略不计。图7 给出了积分法和伽辽金方法求解前四阶杆柱的振型函数曲线，经对比可知，两种方法用于求解杆柱固有频率和振型函数，误差很小，精度较高。

5.2 有杆抽油系统杆柱失稳情况数值分析

有杆抽油系统抽油杆柱的基本参数如表5 所示。实际油井浅则几百米深则几千米，根据前面4.1 节的结果分析，伽辽金方法不适用于求解该长度杆柱的临界载荷，只能采用有限差分法。其不同杆长下临界载荷情况如表6 和图8 所示，其对应失稳变形情况如图9 所示。

图7 杆柱各阶振型函数曲线

图7 杆柱各阶振型函数曲线(续)

表5 基本参数

表6 失稳临界载荷

图8 失稳载荷随杆长变化曲线

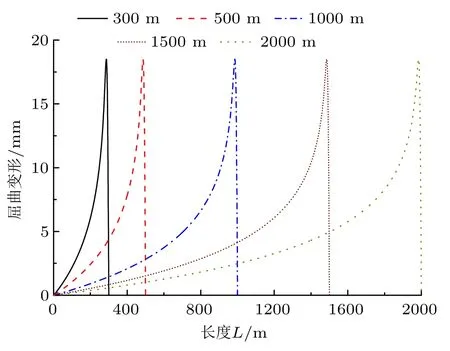
图9 杆柱不同杆长下的失稳变形曲线

由表6 和图8 可知，对于杆柱长度300 ～2000 m的杆柱，考虑分布轴向力和不考虑分布轴向力，其失稳临界载荷相差甚大，因此油田抽油杆柱求解偏磨临界载荷时，分布轴向力不宜忽略不计。

由图8 进一步可知，分布轴向力q = 20 N/m，杆柱长度为200 ～2000 m 时，其临界载荷随杆长的增加而逐渐减小，直至趋于一稳定值，变化率区间约为0%～13.6%。说明200 m 的杆柱代替2000 m 杆柱计算临界载荷时，最大误差为13.6%。由此给出工程建议，在精度要求不太高的情况下，考虑分布轴向力的有杆抽油系统，求解杆管偏磨临界载荷时可以以200 m 左右的杆柱代替几千米的情况进行计算。

由图9 可知，不同井深下，杆柱的失稳变形曲线的规律是近似的，即靠近底端处产生最大失稳变形，这与不考虑分布轴向力时在杆柱的中间位置处产生最大失稳变形有显著不同。因此，抽油杆柱的杆管偏磨严重区域会出现在较深且靠近底端部位，这与文献[16-17] 结论是一致的。

6 结论

本文建立了考虑分布轴向力的细长杆失稳和横向振动的力学、数学模型，通过数值分析结果对比，得出以下结论：

(1)考虑分布轴向力的细长杆柱失稳的必要条件是其横向振动的固有频率为0。该结论是对先前教材的知识点的延伸，同时也适用于不考虑分布轴向力的杆柱失稳情况。

(2) 计算考虑分布轴向力的杆柱受压失稳载荷时，伽辽金近似计算法在求解较长杆柱时超出允许精度范围导致计算结果失真；差分法则适用于求解较长杆柱的失稳载荷，且精度较高。对于端部受拉的杆柱，数值法和伽辽金法计算杆柱固有频率和振型函数的方法都是适用的。

(3)对于抽油杆柱等超长杆，计算失稳临界载荷时考虑分布轴向力是必要的，反之会产生较大的误差。当考虑分布轴向力的超长杆柱(如200 m 以上的抽油杆柱)，其失稳临界载荷随杆长的变化逐渐缓慢减小。精度要求不高时，可不必取杆柱全长，取一部分杆柱计算临界载荷即可。

(4) 本文杆柱与《材料力学》中欧拉杆柱失稳突变处的位置明显不同，这是因为本文模型在欧拉杆的基础上考虑了分布轴向力因素所致。本文对《材料力学》的杆柱静力失稳和《机械系统动力学》的梁的横向振动知识进一步拓展和延伸，并提供了工程应用实例。