Space symmetry of effective physical constants for biaxial crystals∗

Fuan Liu(刘孚安), Zeliang Gao(高泽亮), XinYin(尹鑫), and Xutang Tao(陶绪堂)

State Key Laboratory of Crystal Materials,Shandong University,Jinan 250100,China

Keywords: biaxial crystals,space symmetries,the really positive directions of coordinate axes

1. Introduction

The physical properties of crystals are generally anisotropic and described by tensors. In the current textbooks and literatures,the tensor forms in each point group have been given in matrix forms by symmetry operations in the crystallography coordinate system.[1–4]Because the positive direction of the coordinate axes cannot be given in the crystallography coordinate system,these matrixes are in imaginary quadrant I (x →+,y →+,z →+). Until now, only the positive directions of the piezoelectric coordinate axes have been really defined according to the piezoelectric properties,while the optics, mechanics, and thermology coordinate systems have no definitions. Coordinate transformation is also commonly used in mathematical research.[5–7]For the device applications of crystals, the space distributions of effective physical constants should be studied in detail. Therefore, the signs of the matrix elements must be defined in eight quadrants. Compared with uniaxial crystals, biaxial crystals possess less and lower symmetry components. Most of their properties in eight quadrants cannot be obtained by symmetry operations,which would bring out ambiguities and difficulties in characterization and applications of biaxial crystals. Until now, there are only few literatures concerning signs of the matrix elements and distributions for the nonlinear optical properties in biaxial crystals.[8,9]In this paper,the positive and negative signs of the matrix elements have been given out in each quadrant for biaxial crystals. The distributions of efficient physical constants described with second,third,and fourth tensors and their space symmetry have been discussed. Our results show that most of these distributions are relative to the directions of the coordinate axes. Therefore, we suggest all of the coordinate axes including optics, mechanics, and thermology must be given before the measurements of their physical properties and their applications. This study is expected to contribute to the studies and applications of biaxial crystals since more and more biaxial crystals appear.

2. Signs of matrix elements describing physical properties

A rectangular coordinate system can be established and the space is divided into eight quadrants as shown in Fig.1.

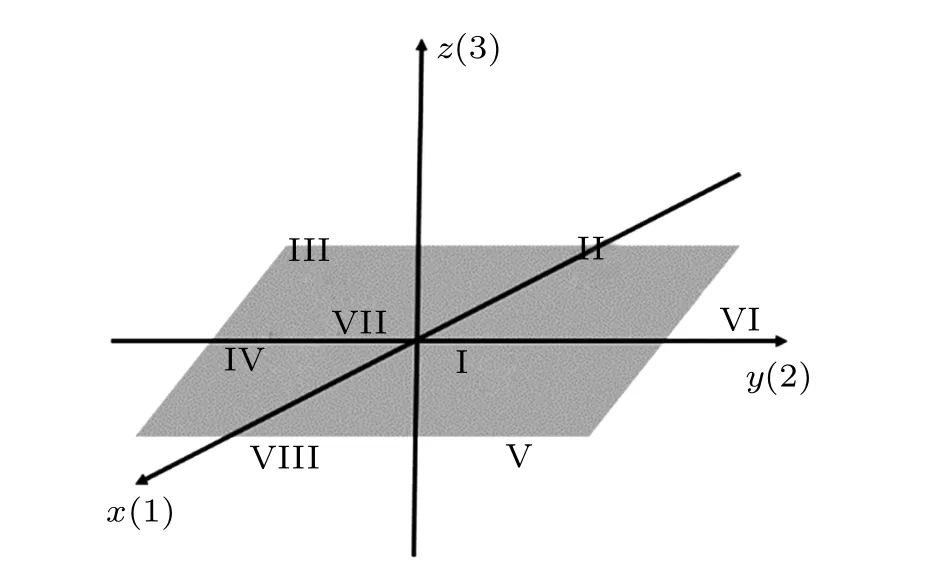
Fig.1. Rectangular coordinate system and eight quadrants.

The positive directions of the coordinate axes are defined in the rectangular coordinate system. Hereby, the subscripts of the matrix elements can be not only x →1, y →2, z →3,but also x →−1, y →−2, z →−3. Then the signs of the subscripts in each quadrant are listed in Table 1.

Table 1. The signs of subscripts in eight quadrants.

Biaxial crystals are limited to orthorhombic,monoclinic,and triclinic systems. Point groups mm2, 222, mmm, point groups m,2,2/m and point groups 1,¯1 belong to orthorhombic system,monoclinic system and triclinic system,respectively.

2.1. Signs of matrix elements for second order tensor

Dielectric property is described with the second order tensor. We take it as an example to study the signs of the matrix elements in eight quadrants.

Table 2. Dielectric matrixes in eight quadrants for monoclinic and triclinic systems.

For point group 2(2‖b),belonging to the monoclinic system, it has a two-fold axis. Herein, the matrix forms are the same in quadrants I,VI;II,V;III,VIII;IV,VII,respectively.In addition, the dielectric matrixes in quadrants II and V can be deduced as follows:

quadrant II: ε−1−1→ε11, ε22→ε22, ε33→ε33, ε−13→−ε13;

quadrant V: ε11→ε11, ε22→ε22, ε−3−3→ε33, ε1−3→−ε13.

The similar process can be used for all of the point groups belonging to monoclinic and triclinic systems. Thus, the dielectric matrixes for monoclinic and triclinic systems are listed in Table 2.

From the results mentioned above, it can be seen that there is one matrix form for the orthorhombic system, two forms for the monoclinic system which appear in adjacent quadrants,and four forms for the triclinic system.Noteworthy,although the triclinic system only has symmetry components 1 or ¯1, there are only four different matrix forms, which are the same in I,VII;II,VIII;III,V;IV,VI,respectively.

The results of dielectric property are suitable for the other properties described with the second order tensors for biaxial crystals, such as electrical conductivity σij, thermal expansionαij,thermal diffusivity κij,and whirly tensor of optical activity properties gij.

2.2. Signs of matrix elements for third order tensor

Different from the second order tensor, the third tensor and its matrix elements take simplified subscripts. We take piezoelectric matrix dijfor example to analyze signs ofthe matrix elements. The subscripts i and j are expressed as 1 →±1,±1;2 →±2,±2;3 →±3,±3;4 →±2,±3;5 →±1,±3;6 →±1,±2;and −1 →±1,∓1;−2 →±2,∓2;−3 →±3,∓3;−4 →±2,∓3;−5 →±1,∓3;−6 →±1,∓2. Similar to the analysis of the dielectric matrix,the matrix forms of dijin the eight quadrants are listed in Table 3.

Table 3. Piezoelectric matrixes in eight quadrants for biaxial crystal.Orthorhombic system

Monoclinic and triclinic systems

From the results in Table 3, it can be seen that there are two matrix forms in the orthorhombic system, four matrix forms in the monoclinic system, and eight matrix forms in the triclinic system. As only the absolute values of efficient physical constants are considered in practical applications,so the negative sign in front of the matrix can be ignored in Table 3. The amounts of different forms are equal to those of the second order tensors.

The results of piezoelectric matrix dijcan be extrapolated to the other properties described with the third order tensors such as electro-optic propertyγij, second-order nonlinear χij,piezoelectric rigidity properties eij,and so on.

2.3. Signs of matrix elements for fourth order tensor

Both simplified subscripts of the fourth order tensor and matrix elements can be expressed as that of subscript j in piezoelectric tensor. And the forms of the matrix forms such as elastic constants sijare listed in Table 4 according to the similar analysis for the second and third order tensors.

Table 4. Elastic matrixes in eight quadrants.

Table 4. (Continued).

From the analysis of Table 4, we can see that the variations of the elastic matrix forms are the same as those of the second order tensor,and it can be extrapolate to the other properties described with the fourth order tensor, such as elastic rigidity property cijand elastic-optic property πij.

3. Space symmetry of efficient physical constants

3.1. Space symmetry of efficient physical constants described with second order tensors

The effective dielectric constants for the monoclinic system can be obtained by coordinate transformation method and presented as

quadrant I:quadrant II:

where the rotation angles are limited as 0 ＜θ ＜90◦,0 ＜ϕ ＜90◦. The distributions are shown in Fig.2.

Fig.2. Distributions of effective dielectric constants for monoclinic system.

Equations (1), (2) and figure 2 indicate that the distributions of the effective dielectric constants in adjacent quadrants I and II are nonsymmetric,which is caused by matrix element ε13.Its maximum and minimum values are located in quadrant I and quadrant II, respectively. From Table 2, it can be seen that there are only matrix elements ε11,ε22,ε33and no ε13in the orthorhombic system and their distributions are symmetry in the eight quadrants. For the triclinic system,the differences are caused by the elements ε12, ε13, and ε23. There are four kinds of distributions in the eight quadrants, which are fit for symmetry center operation.

The above analyses are suitable for all the properties described with the second order tensor,such as σij,αij,κij,and gij.

3.2. Space symmetry of the efficient physical constants described with third and fourth order tensors

quadrant II:

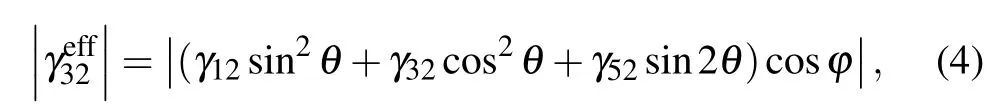
where θ and ϕ (0 ＜θ ＜90◦, 0 ＜ϕ ＜90◦) are the rotation angles around y and z,respectively.

quadrant II:

quadrant III:

quadrant IV:

The results obtained above are suitable for the other physical properties described with the third and the fourth order tensors. They are useful for the physical properties such as photorefractive, phase modulation, space light modulation,optical activity, piezoelectricity, elastic-optics and nonlinear optics. One should pay special attention to that the angels contained in the effective nonlinear coefficients are under the phase match conditions.

Fig.3. The schematic graphs of properties distributions in space and projection in x–o–y plane for biaxial crystal.

Table 3, equations, and figure 3 indicate that there are symmetry elements for the property distributions. For the orthorhombic system,three symmetric planes respectively locate in three coordinate planes x–o–y, x–o–z, and y–o–z. For the monoclinic system, a two-fold axis is along the b axis and a symmetry plane locates in the z–o–x coordinate plane. For the triclinic system,the coordinate point is a symmetry center.

Therefore,to study the physical properties of biaxial crystals, the quadrants in which samples cutted should be clear,and all the matrixes elements should be given in different quadrants. Otherwise, the ambiguities and incorrect matrix elements values for properties will emerge.

4. Suggestion of definitions of positive direction of coordinate axes

To describe the physical properties accurately, the positive directions of the coordinate axes must be defined firstly. It is known that only the positive directions of the electric coordinate axes(dielectric,piezoelectric,elastic,and conductivity)are defined according to IRE standard. We find that these definitions of coordinates axes and their positive directions are suitable for those of thermal properties,which include thermal expansionαijand thermal diffusivity κij.

The definitions of the optical coordinate system for biaxial crystal tell us that the optical coordinate axes x, y, z are the principal axes of the refractive indices and they obey the arrangement nz>ny>nx. The positive directions cannot be given in this definition yet. So, we suggest they should be given with the aid of the piezoelectric coordinate system.

For the orthorhombic system,the optical coordinate axes are parallel to the crystallographic axes. The positive directions of the optical coordinate axes which are parallel to the c axis are defined by d33and d36for points groups mm2 and 222,respectively,and these of a and b axes do not need to define.

For the monoclinic system, the positive directions of the optical coordinate axes obey the right-hand rule. When four fingers rotate from c to a axes(c ＜a)along β,the direction of the thumb is that of the optical coordinate axis which is parallel to the b axis. The other two optical coordinate axes are located in c–a plane as shown in Fig.4. For point 2, it is not necessary to define the directions of the other two optical coordinate axes. For point m, another optical coordinate axis is located in c–β–a area and near c axis. Its positive direction can be defined by d33. Where after, the direction of the third optical coordinate axis is defined according to the right-hand rule.

Fig.4. Positive direction definitions of optical coordinate axes for monoclinic and triclinic systems.

5. Conclusion and perspectives

The positive and negative signs of matrix elements describing physical properties in each quadrant have been given for biaxial crystals. The space distributions of the effective physical constants described with every order tensor and their space symmetries also have been discussed. To avoid the errors and difficulties in researches and applications of biaxial crystal properties, the definitions of the positive directions of the coordinate axes have been suggested. These results can be used for all the crystal physical properties of biaxial crystals except center symmetry crystal. The above conclusions are expected to contribute to study crystal properties and explore new crystal materials. We think it is an addition of current crystal physical textbooks.