Effect of radiation on compressibility of hot dense sodium and iron plasma using improved screened hydrogenic model with l splitting

Amjad Ali, G Shabbir Naz, Rukhsana Kouser, Ghazala Tasneem, M Saleem Shahzad,Aman-ur-Rehman, and M H Nasim

1Department of Physics and Applied Mathematics,Pakistan Institute of Engineering and Applied Sciences,Islamabad 45650,Pakistan

2Department of Nuclear Engineering,Pakistan Institute of Engineering and Applied Sciences,Islamabad 45650,Pakistan

Keywords: self-consistent-field methods,thermodynamics of plasmas,average atom model,shock Hugoniot calculation

1. Introduction

Studies of high pressure phenomena have shown tremendous advancement in recent decades by achieving dynamic high pressure up to 1 TPa (～10 Mbar, 1 bar = 105Pa)and corresponding compressions in materials up to ten times initial liquid density and temperatures up to several thousand Kelvins. These extreme conditions are achieved by means of single-shock, multiple-shocks,[1-3]and isentropic compressions.[4-6]These shock waves are the subject of vast interest in flyer plate experiments,exploding of wires and foils by exposure of high currents,high-power x rays produced by Z-pinch plasmas, the high power laser ablation experiments,and laser-matter interaction in inertial fusion experiments,etc.These high pressure studies have proven that during compression, the electric and magnetic properties of material change dramatically in addition to phase transitions of materials. The emergent phenomena and technologies of high pressure studies are very vast and have opened new horizons to discover and study materials under extreme conditions of pressure and temperature that are typically found in planets and stellar interior. In context of dense plasma systems, these high pressure studies have given birth to a new research area called high energy density systems(HEDS)and the corresponding branch of physics that explores HEDS is named as high energy density physics (HEDP). HEDS are the systems having energy density ≥1012erg/cm3(1 erg=10−7J)which corresponds to a pressure of 106bar(1 Mbar),typically found in the cores of giant planets, in inertial confinement fusion(ICF)experiments,and in intense ion-beam, electron-beam or high power lasermatter interactions experiments.[7,8]This wide occurrence of HEDS covers more than,the so-called dense plasma regime in density-temperature phase space. This is due to the fact that a low density (less than solid density) and high temperature plasma can have a pressure equal or greater than 1 Mbar.[9-11]

The high pressure dynamic phenomena generally encountered in HEDS are regarded as hydrodynamic phenomenon and simulated by hydrodynamic equations. Hydrodynamic simulations are used in modeling,analyses,and diagnostics of experiments in HEDS regime,particularly to predict the spaceand time-dependent density-temperature profiles.To close the set of hydrodynamic equations(i.e.,conservation of mass,momentum,and energy),an accurate,smooth,and thermodynamically consistent equation of state (EOS) data is needed.[11]The accuracy and validity of such data entirely depend upon atomic models used to describe the plasma. The atomic models estimate different ionization and excitation processes occurring in plasma. For instance,the energy states of the bound electrons in HEDS are significantly affected due to the electric field of the neighboring ions as atoms come very close to each other. Due to these density effects, two important phenomena arise in dense plasmas,named as pressure ionization(PI)and continuum lowering(CL).The PI is the shifting of bound electrons to continuum due to pressure exerted by neighboring atoms at high densities,and the CL is the reduction in binding energy of electrons due to interaction of degenerate bound and free electrons. These two phenomena are essentially required in EOS modeling for electronic structures of HEDS.

The EOS describes fundamental thermophysical properties of matter. The EOS has a substantial interest for its fundamental research in shock wave experiments and has a wide range of applications.[6,12-19]States of material accessed by HEDS experiments span a wide region in the phase diagram.For instance, it covers hot compressed matter, strongly coupled plasmas,and degenerate plasma. In the context of HEDS simulation based on theoretical models, the EOS has its fundamental importance because of its essential requirement in hydrodynamic equations. Different models of EOS containing ionic contribution and electronic contribution are presented in some of literature.[20-26]Efforts were made to develop more and more accurate detailed descriptions of ionic as well as electronic parts of EOS.[16-19,27-32]

The EOS data are primarily consists of contributions from electrons and ions along with those from cold part solids, i.e., empirical calculations for pressure and energy at T =0 K. There are separate models for calculating electronic and ionic contributions. In this paper, the EOS model is developed in comparison to electronic contributions from I-SHML model[26,33]and ionic contributions from Cowan model, whereas the cold part contributions are obtained from the scaled binding energy model(SBEM).[34]For authenticity and applicability of EOS,shock Hugoniot calculations are performed using EOS data. The rest of this paper is organized as follows. In Section 2 we introduce the basis EOS and its link to thermodynamics. Section 3 describes the electronic contributions to EOS.The theoretically developed EOS formulation based on I-SHML model is presented in Section 4. While the ionic contribution to EOS is described in terms of the Cowan model in Section 5. The cold component is taken from the scaled binding energy model in Section 6.

2. Essential thermodynamic relations for EOS development

The EOS gives the information about state of the system under the applied conditions of thermodynamic variables. In mathematical sense, the EOS is a fundamental property of a thermodynamic system which can be characterized by an extensive functional form like

G(u,v,w)=0,

where the variables u, v, and w can be any thermodynamic variables such as volume V,pressure P,entropy S,internal energy E or temperature T. They may be in the form of tables relating different thermodynamic variables or in the form of graphs.

The EOS is formulated by constructing partition function Z of the systems constituting electrons and ions. In considering hot dense matter,electrons and ions are treated as separate entities, and hence they require different partition functions.In this way the temperature of electrons and ions can take,in principal, two different values. But under LTE conditions,they are assumed to be the same with a superficial assumption that the contribution of electrons and ions under equilibrium is additive to sufficient accuracy,which may not be true in general.[35]Conventionally, thermodynamically consistent variables are calculated from Helmholtz free energy calculations derived from the partition function Z of the system under considerations. Ions and electrons for EOS calculations are treated as separate entities each having its contribution for Helmholtz free energy F, pressure P, internal energy E, entropy S,specific heatsCvat constant volume and constant pressure Cpof the system. The total EOS can be written as

where Ftotis the total Helmholtz free energy. Fcis the contribution of Helmholtz free energy from cold curve,while Feand Fiare the components of Helmholtz free energy due to electron and ions respectively. From this construction, the thermodynamic variables can be separated for electrons and ions,i.e.,

From Helmholtz energy the thermodynamic variables can be calculated as follows:[20,35]

The specific heat at constant volume is represented as[17]

3. Electronic contribution to EOS

4. The electron EOS formulism using I-SHML model

The Fboundrepresents the contribution of bound electrons to Helmholtz free energy and has the form in the I-SHML context as

where Zi, Pi, and Direpresent average atom values of level screened charge,occupation number,and level degeneracy respectively which are obtained from the I-SHML.Similarly the contribution of free electrons to Helmholtz free energy Ffreesimplifies as[26]

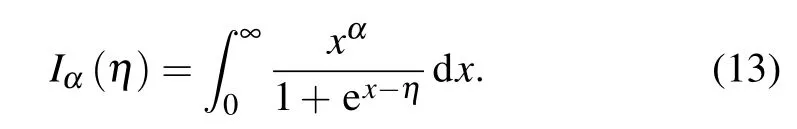
Finally, the part of the interaction energy of bound and free electrons to Helmholtz free energy Fbound−freeis given by[26]

By using the definition of pressure from Helmholtz free energy one has a total electron pressure Peconsisting of corresponding three parts as

where Pboundis the pressure amounting for bound electrons[26]

Here

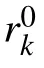
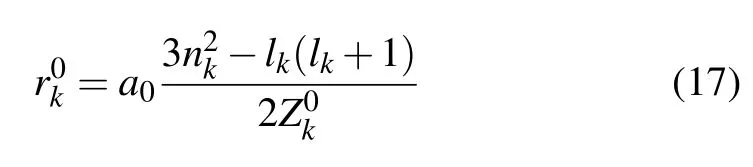
with a0as Bohr radius(in unit of cm)and Rwsis the Wigner-Seitz radius(in unit cm)defined as

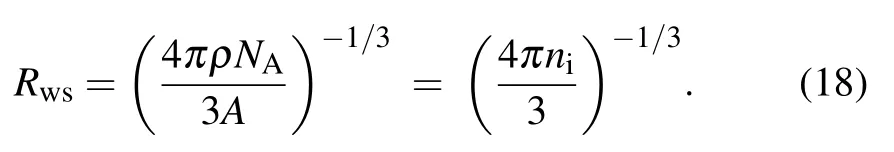
Here nias the ions number density(in units of ions/cm3),NAis the Avogadro number,and A is the molar mass of the element.Similarly,the pressure for free electron Pfreewill become

Finally the pressure resulting from the interaction of bound and free electrons will be Pbound−free

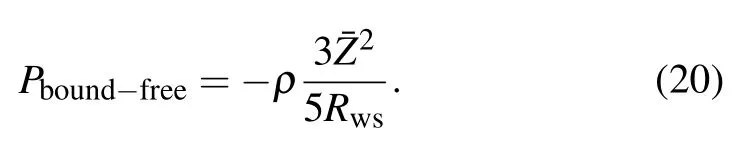
The same analysis goes for total electron energy Eeas this can also be expressed in terms of Feas

This also consists of three parts: energies from the bound electron Ebound,free electron Efree,and bound-free interaction Ebound−freeas expressed below:

On the same lines using the definition of entropy from Eq.(8),the electronic contribution to entropy using the I-SHML model will be

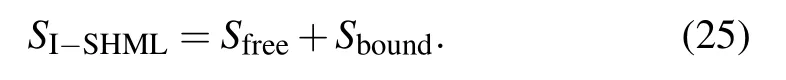
The entropy of bound electrons Sboundbecomes

and that of free electrons Sfreetakes the form as

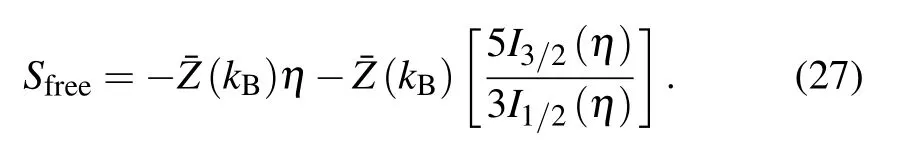
From Eq. (9), the specific heat at constant volume comes in the I-SHML formulism as

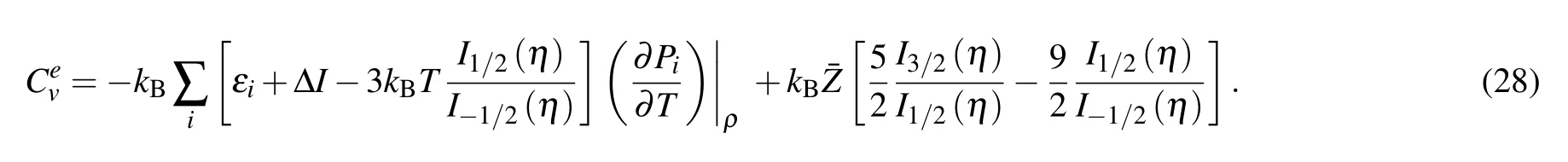
Here εiare level energies and ΔI is continuum lowering energy. The terms ∂Pi/∂T and ∂Pi/∂ρ in Eq.(28)are computed by solving the matrix equations

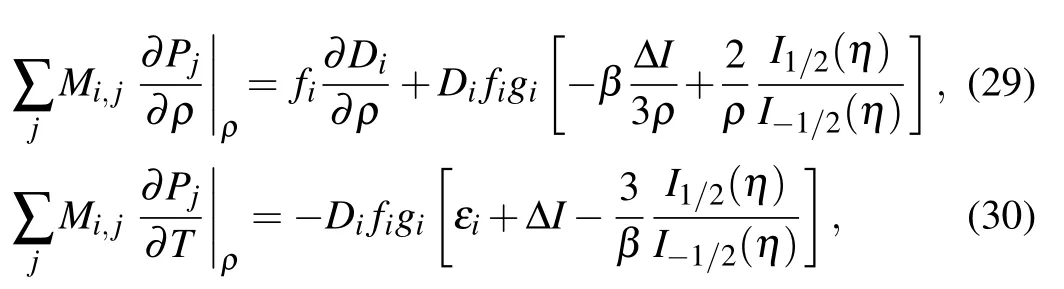
where the anti-symmetric matrix M is defined as

5. Ionic contribution to EOS: Quotidian equation of state

The quotidian equation of state (QEOS) is an empirical general-purpose equation of state model used in hydrodynamic simulation of high-pressure phenomena developed by More et al.[35]This model assumes only two phases of matter,namely,fluid phase(for liquid and gas phases)and solid phase.Moreover, phase transitions of material are not incorporated.These simplifications in QEOS are made by using empirical scaling laws governed by combining Debye, Gruneisen, and Lindemann laws for thermodynamic properties like Helmholtz energy, pressure, energy, and entropy for both fluid and solid phases separately. The ionic form for Helmholtz free energy Fe,pressure Pe,and energy Eecan be written in terms of scaling function f(u,w)laws as

where the scaling parameters u and w are obtained from Debye temperature θDand melting temperature Tmas

The distinction between solid and fluid is made by imposing assumptions based on values of u and w. For fluid one has w ＜1 while solid is divided into two categories: a high temperature solid u ＜3 and w ＞1,which we will consider in this research and low temperature solid u ＞3 and w ＞1.

To complete the model, More[35]purposed empirical relation for density-dependant Debye temperature θD, melting temperature Tm,and Gruneisen parameter as

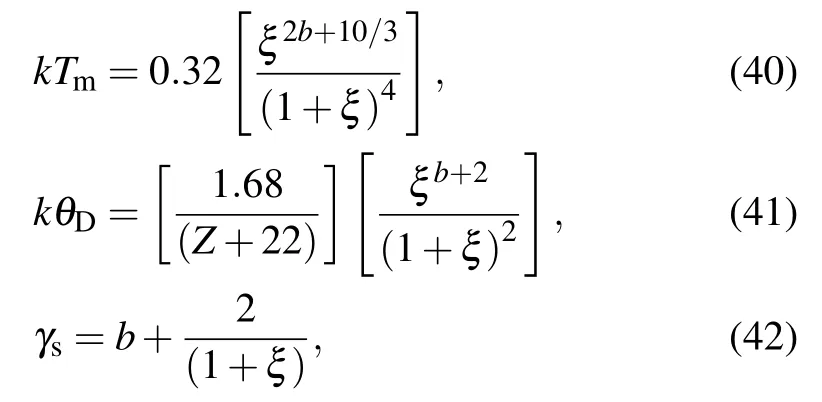
where the terms have the following meanings:

The corresponding scaled thermodynamic variables in high temperature solid are given below

6. Cold curve contribution to EOS:Scaled binding energy model

To compensate the ionic cold part of EOS, a recent progress in the ion equation of state model is made by the development of the scaled binding energy model. This model gives a very good description of the solid phase and provides a better model for density-dependant Grunesien parameter and melting temperature for the solid phase. The SBE model,[62-64]as the name suggests, uses a scaling parameter“a”to model the binding energy at zero temperature(cold energy curve)of any material using some scaling function. The scaling parameter a is the ratio of separation of ions from normal radius to scaled length of the material which are defined as

and l is material characteristic scale length given by

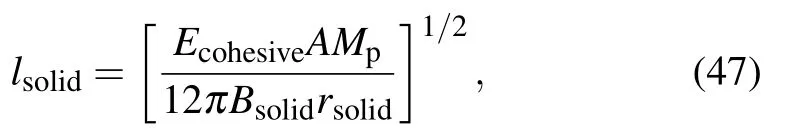
where Ecohesiveis the cohesive energy of the material, rsolidis normal radius of the ion obtained from Wigner-Seitz radius at normal density, and r is the radius obtained from Wigner-Seitz radius at density under consideration. The cold energy is given in terms of scaling function ε(a)as

and the cold pressure derived from the cold energy takes the form as

With the help of scaling parameter a,a universal SBE curve is constructed using four fitting parameters s1, s2, s3, and s4as follows:

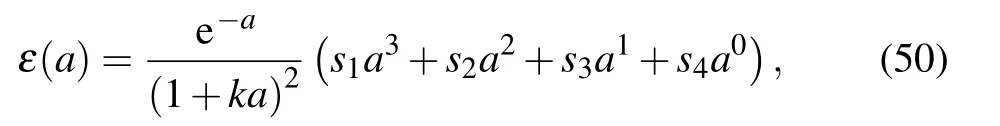
where k is the compressibility given as

The four fitting parameters s1,s2,s3,and s4are computed with constraints on the derivative of the SBE with respect to a which are as follows:

where B′Solidis the pressure derivative of the bulk modulus at solid density and at zero temperature which is determined experimentally. With these constraints the fitting parameters s1,s2,s3,and s4become

7. Radiation energy density contribution to EOS

At high densities and temperatures, matter exists in plasma state. In HEDS shock experiments, the electrons in the hot dense plasma emit radiations due to rise in temperature via bremsstrahlung and also reach equilibrium with the plasma via inverse bremsstrahlung and Compton scattering processes. In principle, a radiation-dependant ionization model for plasma is required to simulate the radiative transfer phenomenon in which radiation temperature and plasma temperature are treated on different footings. From this radiationdependant ionization model the EOS could be formulated that can describe the radiation-matter interaction. The effect of radiation on plasma environment mainly depends upon the optical thickness of the material which is calculated from the solution of the radiative transfer equation. In literature, various models are presented for radiative transfer problem but most of them are limited to diffusion approximation solution to radiative transfer problem in which radiation temperature and plasma temperature are assumed to be equal. Another reason for this approximation comes from the fact that the time scale for the equilibration of radiation with matter is generally of the order of 10−13s to 10−15s. This time scale is in no comparison with the time scale of shock propagation which is 10−9s to 10−6s. With this justification, it can be assumed that matter exists in equilibrium with radiation field.Under equilibrium condition, the energy density of radiation depends on the radiation temperature which is equivalent to material temperature. This means that under equilibrium conditions one can explicitly add radiation energy in EOS without radiation-dependant ionization model. When an intense shock is launched, the temperature becomes so high that the energy density and pressure of radiation become comparable to the internal energy and pressure of electrons,thereby affecting both the EOS and Hugoniot. The energy density of equilibrium radiation can be obtained using Stefan-Boltzmann law. Then,the energy density of radiation is given

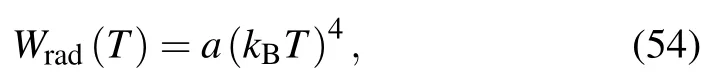
where the value of radiation constant a=137.999 when kBT and W are expressed in keV and 1012erg/cm3, respectively.From this equation one can find the specific energy for a given density ρ as

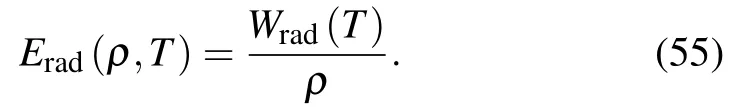
Similarly,pressure can be derived as

In the presence of radiation,the total specific energy and pressure of electron-radiation system are given by

8. Shock wave and Rankine-Hugoniot relations

In HEDS where there is deposition of huge energy over very short dimension and in a short time which leads to propagation of abrupt disturbances in materials;called shock waves and prove to be a favorable candidate for analysis of HEDS.The material subjected to a strong shock wave is compressed,heated, and ionized which leads to generation of discontinuities in thermodynamic quantities of the material after the shock. This discontinuous behavior in thermodynamic quantities is studied with the help of well-known Rankine-Hugoniot(RH)equation.The standard form of Rankine-Hugoniot equation is given as

where the subscript 0 refers to quantities behind the shock and the subscript 1 used for those after the shock. The Rankine-Hugoniot equation is basically a form of energy conservation law across the discontinuity and its solution is called shock adiabat or Rankine-Hugoniot curve. The Hugoniot curve or shock adiabat does not describe the trajectory of the shockcompressed material in pressure-volume space as it is undergoing the shock compression. Rather,the Hugoniot curve describes a locus of points for the equilibrium pressure behind the shock for a given compression and initial conditions.

The solution of Rankine-Hugoniot equation is solely dependent on initial conditions. If initial conditions are specified then the system is left with only three equations and four unknowns, i.e., u1, E1, P1, and V1. Hence another relationship is required for unique solution (four equations and four unknowns)of the system. From this point onward, Rankine-Hugoniot equations are solved either with the help of experimental data or by using analytical or tabular EOS. For simplicity,some assumptions are applied,i.e.,P0=0,E0=0,and u0=0.

9. Results of computation for Hugoniot curve

The Hugoniot curve is the locus of points for the equilibrium pressure behind the shock for a given compression and given initial conditions. This means that there would be a different curve for different initial conditions. In actual calculations, shock Hugoniot calculations are very much sensitive to the physics of ions and electros involved in EOS calculations, for instance the inclusion of bound electron structure in EOS shows the shell structures in shock Hugoniot calculations. These shell structures arise due to quantum mechanical treatment of bound electrons which is a subject of great interest in high pressure studies. In this study, the effect of radiation on shock Hugoniot case is studied under LTE conditions and is compared with the case where there are no radiation present in the system. The Hugoniot calculations are performed by taking sodium and iron as test cases. The initial conditions for computations are taken at ρ = ρ0(solid density),kBT0=0.0025 eV=300 K(room temperature)and with additional constraint on total pressure Ptot(ρ0,T0)=0.0 for sodium and iron. The Hugoniot profiles for pressure, energy,and temperature are plotted against the compression ratio ξ =ρ/ρ0. The asymptotic compression limit ξlimitachieved by Hugoniot method can be estimated by assuming full ionization gas model having γ as specific heat ratio which is blown by single shock of infinite extent as[65]

In this study the electronic contributions to EOS are based on screened hydrogenic model that predicts the electron thermodynamic domain for pressure, energy, and temperature where RH curves strongly depend on the electronic shell structure. These shoulders in electronic shell structure corresponds to the occurrence of ionization in successive shells. The basis of formation for these shoulders or shell structures is due to the release of bound electron energy stored in shells which is affected by pressure of free electrons present in the vicinity. It happens beyond solid density when ionization starts to increase due to pressure ionization and continuum lowering phenomenon. At this point the shock energy increases which increases ionization process,i.e.,it depopulates the successive low energy electronic levels which eventually result in further compression of the material.The increase of ionization results in increase of the free electron pressure as well which consequently compensates the on going compression. This balancing process goes on, up till the density of the system reaches the single infinite shock compression density which is 4 times that of solid density. It is due to the fact that the maximum compression in density of any solid material from a shock of an infinite strength can reach 4 times of its solid density.[65]In absence of radiation field, all the energy delivered by the shock is consumed in increasing the kinetic energy of the electrons. The increase in kinetic energy of the electron raises the temperature of plasma which results in onset of thermal ionization. With strong shocks higher temperatures are achieved for which free electron gas model(full ionized plasma)can be applied. Free electron gas is assumed to be monoatomic gas having γ =5/3. Using this value of γ in Eq. (60) gives the limiting value ξlimit=4 in the absence of radiation field.

In the presence of radiations(owing to Eq.(54))changes the scenario of the energy deposition of the electron-radiation system is assumed to be under LTE conditions. Under these conditions,the radiations start playing a dominant role in energy deposition and compression at T ～1 keV and densities around ξ ～4. This is due to the reason that when radiations are present in the system, the energy imparted by the shock will be used not only for increasing temperature of free electrons but also used for compression of the material. As long as bound electrons are present in the system there is competition between bound electron energy and free electron energy.Due to which,less pressure is required to compress the material for same density as compared to fully ionized case. Which means that near full ionization(where number of bound electron is negligible), the radiation pressure will be comparable with free electron pressure and there will be a competition between the two forces onwards. After full ionization, radiation pressure dominates,which further compresses the material by increasing energy density of the system as the fourth power of temperature. At this point, free electron pressure is negligible in comparison with radiation pressure, and radiation field in this domain can be treated as photon gas having effective γrad=4/3. The compression by radiation goes on RH curve till it reaches its limiting compression ratio limit of value 7 which is predicted by Eq.(60)using γrad=4/3. These facts are clearly evident in our indicated calculation results for sodium and iron listed below.

Fig.1. Comparisons of pressure Hugoniot results of this study (with radiation (sea green) and without radiation (wine)) for sodium with results by Zhang et al.in Ref.[66]with radiation(olive)and without radiation(pink).The data are taken from Fig.1 of Ref.[66].

The comparison is made in Fig.1 with a recent study by Zhang,[66]in which sodium is taken as an example to show the effect of radiation on shock Hugoniot using molecular dynamic simulations. The results of sodium Hugoniot calculations are compared with Ref.[66]in Fig.2 which shows very good agreement.Sodium Hugoniot calculations are performed by taking solid density being equal to 0.986 g/cc, bulk modulus as 6.43 GPa,pressure derivative of bulk modulus at zero temperature and solid density as 3.84 and cohesive energy as 1.0126 eV/atom. The pressure ionization parameters are taken from Ref. [26] having azm=3.5 and bzm=1.0. The pressure Hugoniot with radiation shows higher value of maximum compression limit ξlimitof value 7 as compared to compression limit of value 5.5 for the system without radiation. The Hugoniot profiles for energy and temperature are plotted in Fig.3 and Fig.4 respectively. The Hugoniot pressure and energy profiles for the system without radiation are drawn along with pressure and energy isotherms in Figs. 5 and 6 to elaborate the evolution of Hugoniot profiles without radiation effect. Similarly,the evolution of radiation effects on Hugoniot profiles for pressure and energy are presented in Figs.7 and 8 respectively. A three-dimensional representation of the electronic specific heat at constant volume for sodium from EOS is shown in Fig.9. The electronic specific heat at constant volume along the shock Hugoniot is plotted in Fig.10.

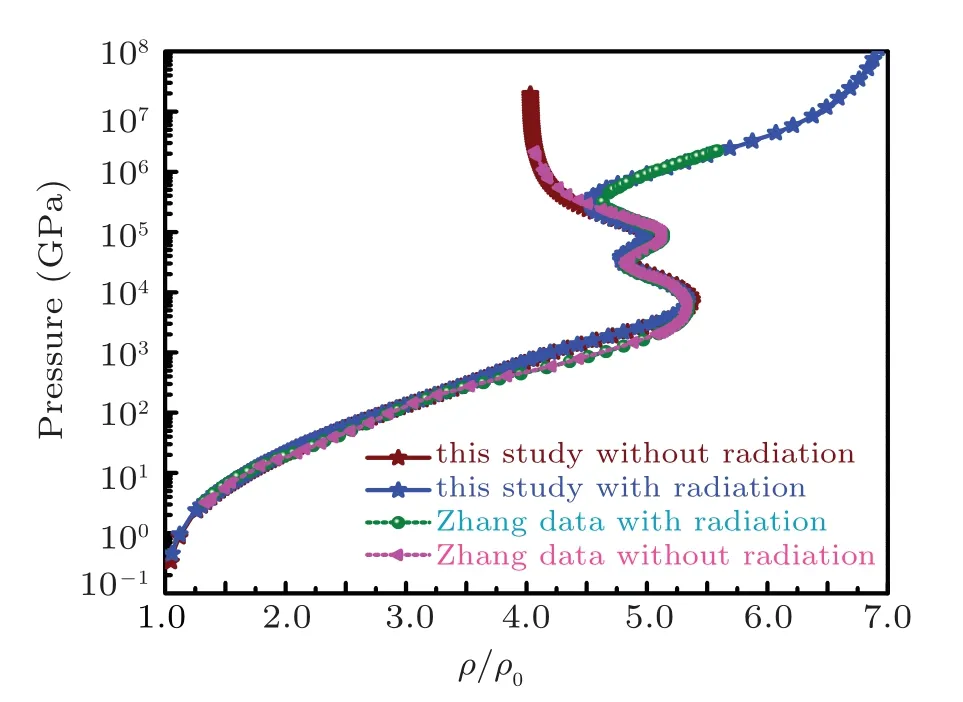
Fig.2. Comparison result of pressure Hugoniot of this study(with radiation(blue)and without radiation(wine))for sodium with results by Zhang et al.in Ref. [66] (with radiation (olive) and without radiation (pink). The data are taken from Fig.1 of Ref.[66].

Fig.3.Comparison of energy with and without radiation along shock Hugoniot for sodium.

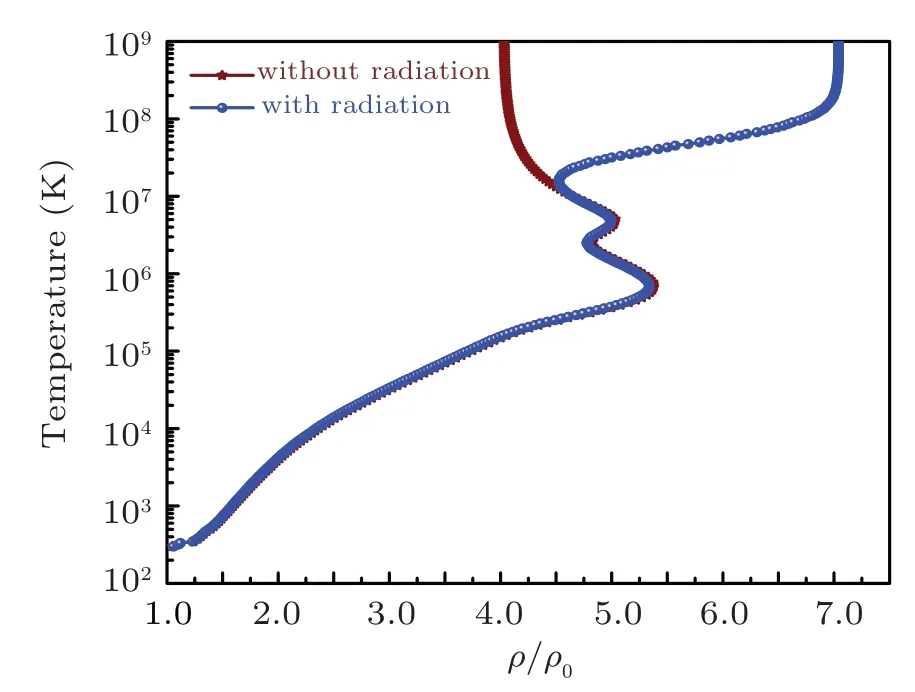
Fig.4. Temperature profile along shock Hugoniot for sodium.

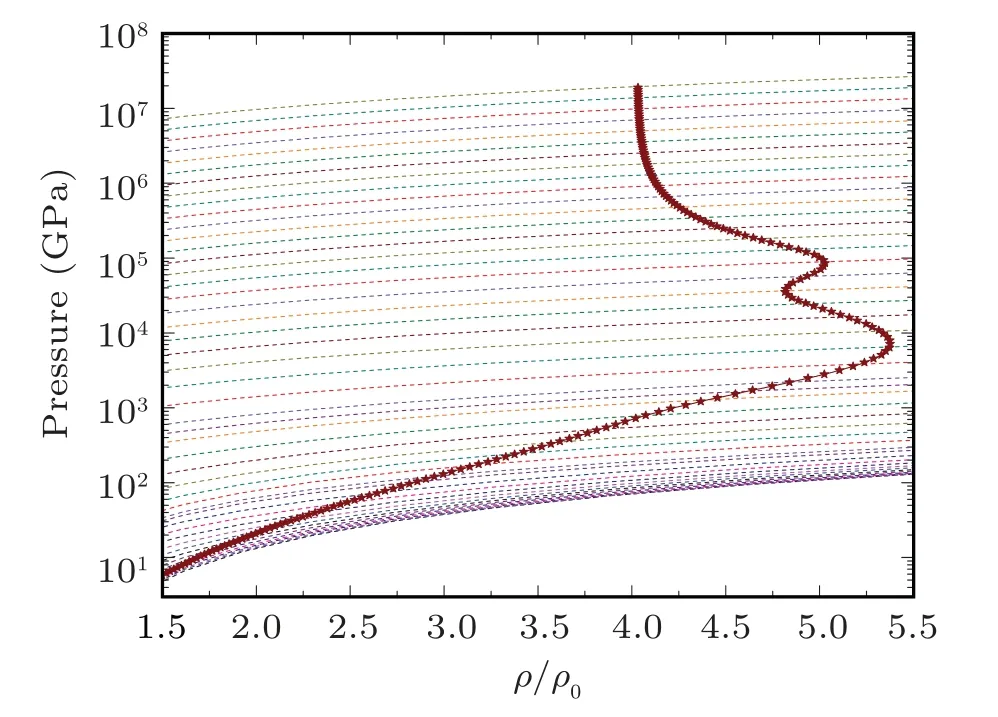
Fig.5. The evolution of the pressure shock Hugoniot profile without radiation inclusion for sodium on pressure isotherms. The Hugoniot profile is drawn with pressure isotherms on background to elaborate the evolution points of Hugoniot profile.

Fig.6.The evolution of the energy along the shock Hugoniot profile without radiation inclusion for sodium on energy isotherms. The Hugoniot profile is drawn with energy isotherms on background to elaborate the evolution points of the Hugoniot profile.

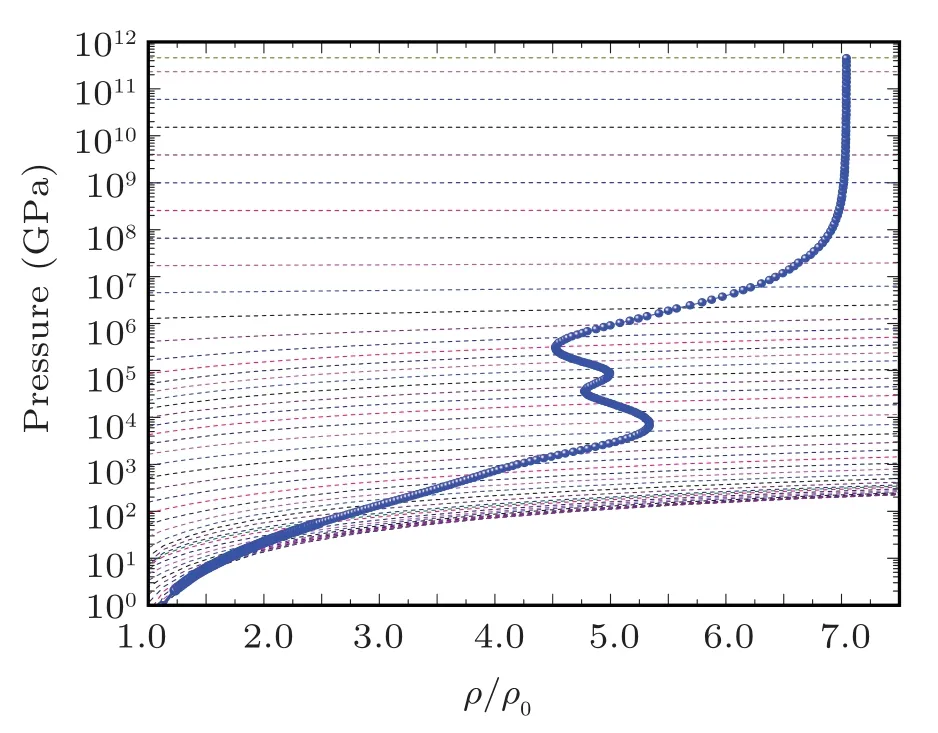
Fig.7. The evolution of the pressure shock Hugoniot profile with radiation for sodium on pressure isotherms. The Hugoniot profile is drawn with electron-radiation system pressure isotherms on background to elaborate the evolution points of the Hugoniot profile.

Study for iron is also accomplished as an extension after sodium analysis. The results of iron shock Hugoniot are compared with Fig.5 of Ref.[60]in Fig.11. Excellent agreement is found and it shows the reliability of our model. In this study the computations are performed by taking solid density being equal to 7.874 g/cc, bulk modulus as 163.4 GPa, pressure derivative of bulk modulus at zero temperature and solid density as 5.38,and cohesive energy as 3.59 eV/atom.

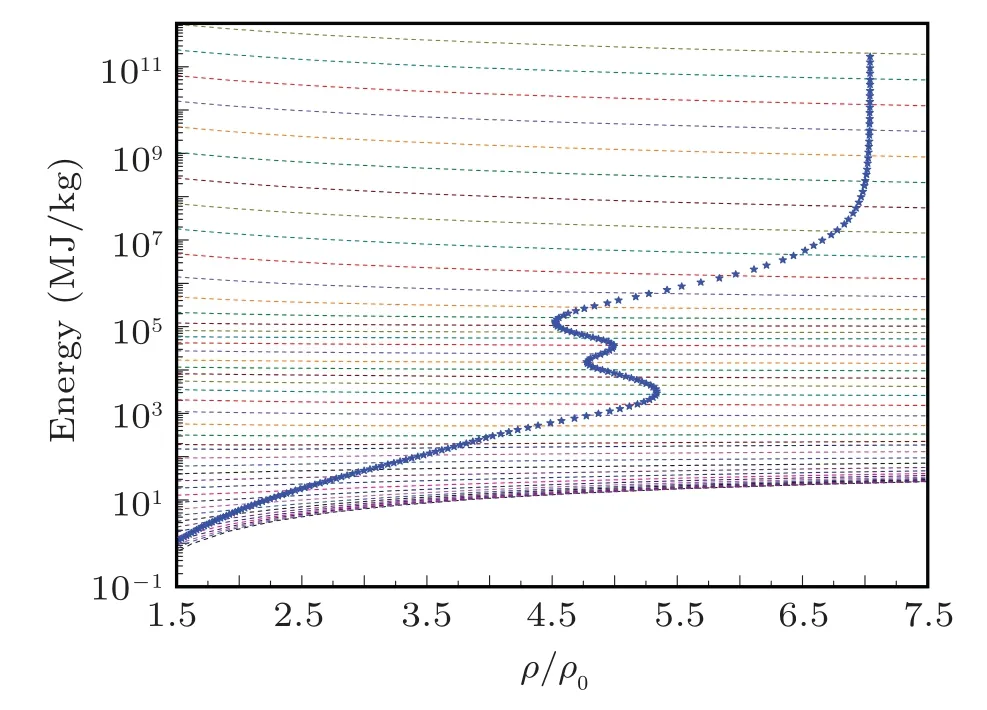
Fig.8.The evolution of the energy shock Hugoniot profile with radiation for sodium on energy isotherms. The Hugoniot profile is drawn with electronradiation system energy isotherms on background to elaborate the evolution points of the Hugoniot profile.

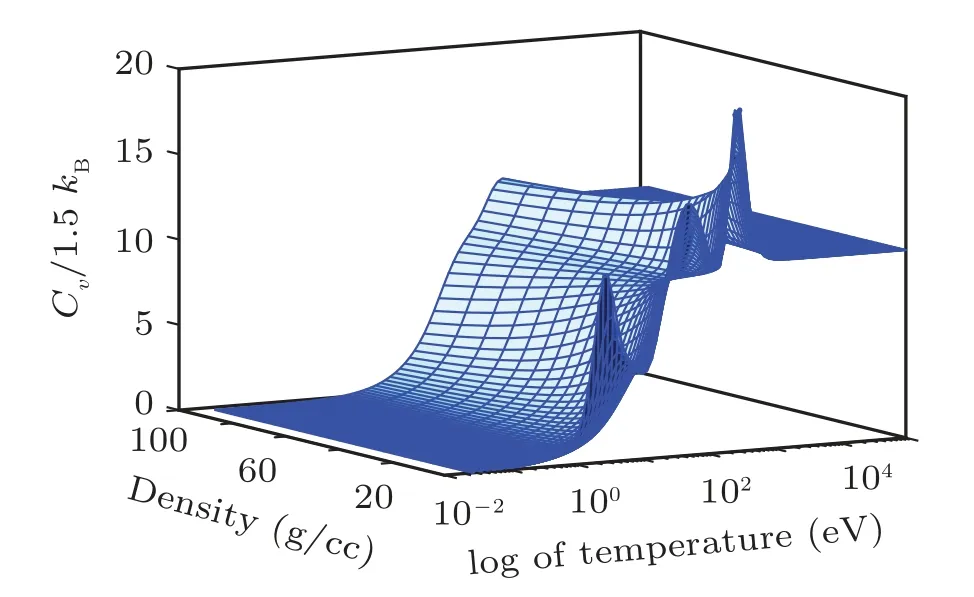
Fig.9. Three-dimensional representation of specific heat at constant volume for sodium against temperature and density grids showing quantum shell structures.

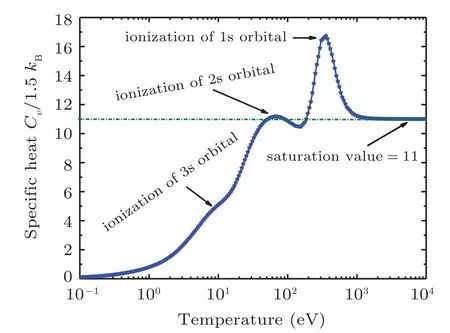
Fig.10. Specific heat along the shock Hugoniot for sodium showing Schottky anomaly.

The Hugoniot profiles for thermodynamic variables pressure, energy, and temperature are obtained and plotted in Fig.12-14 respectively for azm=3.0 taken from SHML model while bzmis taken as 1.0. The Hugoniot pressure and energy profiles are drawn along with pressure and energy isotherms in Figs.15 and 16 to elaborate the evolution of Hugoniot profiles without radiation effect. Similarly, the evolution of radiation effects on Hugoniot profiles for pressure and energy are presented in Figs. 17 and 18 respectively. A three-dimensional representation of the electronic specific heat at constant volume for iron is shown in Fig.19 and along the shock Hugoniot is plotted in Fig.20.

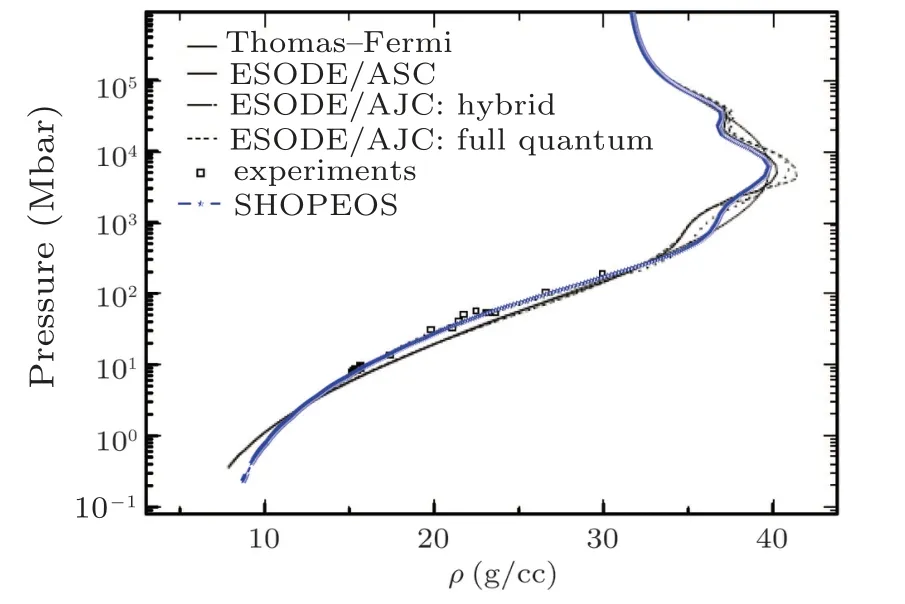
Fig.11. The comparison of SHOPEOS pressure Hugoniot profile with pressure Hugoniot profile of Ref.[60]for iron.

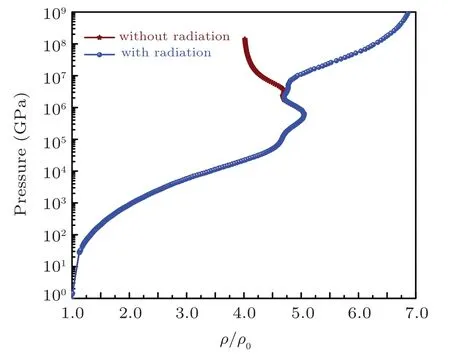
Fig.12. The evolution of the pressure with and without radiations along the shock Hugoniot profile for iron.

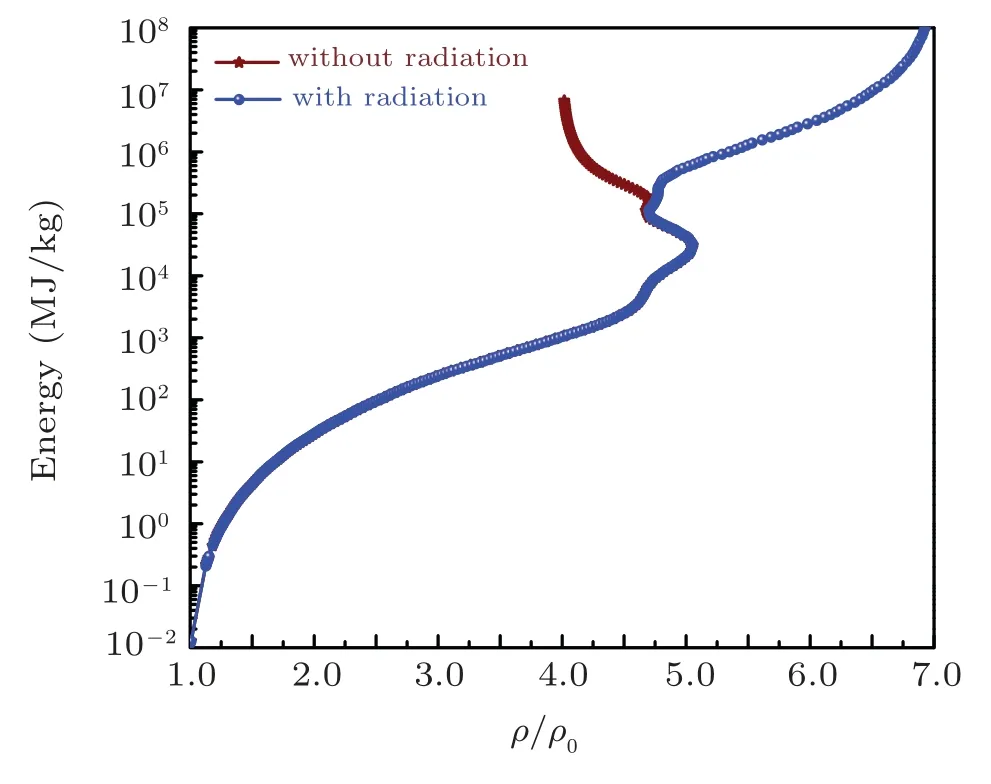
Fig.13. The evolution of the energy with and without radiations along the shock Hugoniot profile for iron.

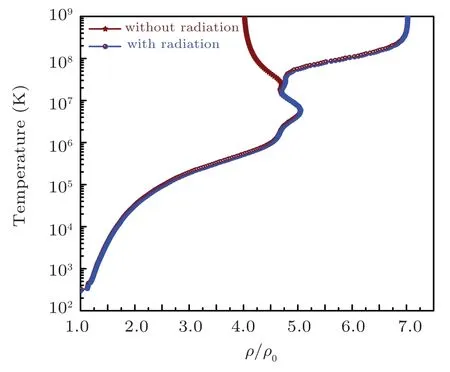
Fig.14. The evolution of the temperature with and without radiations along the shock Hugoniot profile for iron.

Fig.15. The evolution of the pressure shock Hugoniot profile without radiation inclusion for iron on pressure isotherms. The Hugoniot profiles are drawn with pressure isotherms on background to elaborate the evolution points of the Hugoniot profile.

Fig.16. The evolution of the energy along the shock Hugoniot profile without radiation inclusion for iron on energy isotherms. The Hugoniot profiles are drawn with energy isotherms on background to elaborate the evolution points of the Hugoniot profile.

The electronic specific heat at constant volume Cvis also an interesting direct measure of the ionization of successive shells and indirectly measure on the release of energy stored in shells as shown in Fig.10 for sodium and in Fig.20 for iron.The shell structure appears in Cvcalculations after which the Cvsaturates to a constant value of Cv=Z. This phenomenon is called “Schottky anomaly”[67]and is of great interest for experimentalists.

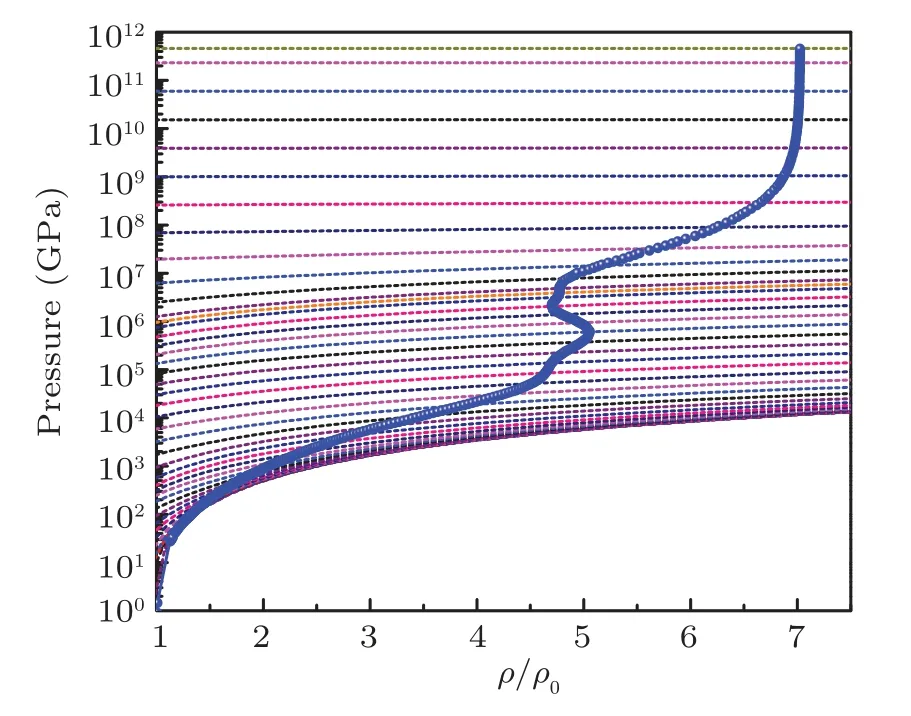
Fig.17. The evolution of the pressure along the shock Hugoniot profile with radiation for iron on pressure isotherms. The Hugoniot profiles are drawn with electron-radiation system pressure isotherms on background to elaborate the evolution points of the Hugoniot profile.

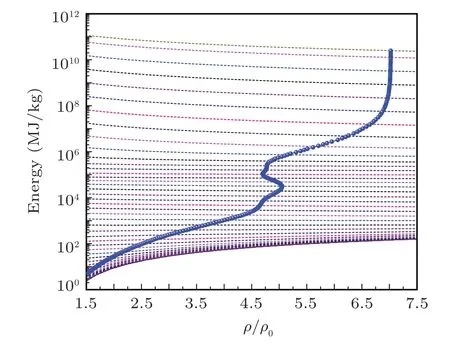
Fig.18. The evolution of the energy along the shock Hugoniot profile with radiation for iron on energy isotherms.The Hugoniot profiles are drawn with electron-radiation system energy isotherms on background to elaborate the evolution points of the Hugoniot profile.

Fig.19. Three-dimensional representation of specific heat at constant volume for iron against temperature and density grids showing quantum shell structures.

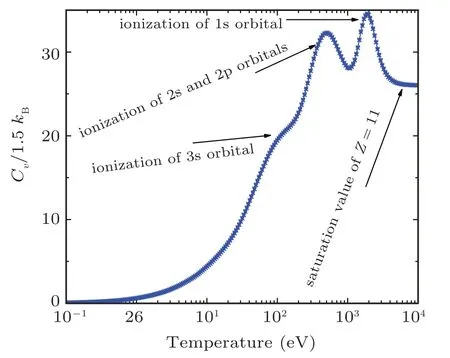
Fig.20. The specific heat at constant volume along the shock Hugoniot profile for iron showing Schottky anomaly.

Figure 10 shows the specific heat at constant volume for sodium. In this figure there are 3 bumps on Cvcurve. The 1st one is observed at 10 eV, 2nd at 80 eV, and 3rd one at 700 eV corresponding to M-, L-, and K-shell electrons, respectively. When both the 1s electrons are ionized, there is a sudden break in the specific heat,which tends to an ideal gas behavior of Z =11 independent particles. It is important to note that the height of peak determines the ionization potential of the shell. The same behavior for the case of iron’s electronic specific heat at constant volume is shown in Fig.20.In this figure there are 3 bumps Cvcurve. The 1st one is at 100 eV, 2nd at 800 eV, and 3rd one at 1200 eV corresponding to M-, L-, and K-shell electrons, respectively. Clearly the full ionization of iron leads the Cvto an ideal gas value of Z =26 independent particles asymptotically. It is important to note that these shell structures are absent in TF theory because it uses semi-classical approximation to solve Poisson equation for electron density. So, inherently, TF theory does not take into account shell description for which one needs to solve Schrodinger equation. These corrections for TF theory are incorporated in QSM model.[21,22,29,31,59-61]For the sake of comparison,iron and sodium shock Hugoniot are plotted in Fig.21.

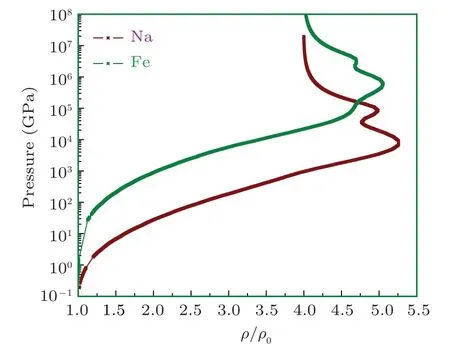
Fig.21. The comparison of iron and sodium Hugoniot profiles.

The shell structures are evident and the values of pressure are different owing to Z and initial solid density values. The pressure ionization parameters are the same as before. Moreover, it should be noted that the shock-wave data analysis allows one to investigate the material properties in very wide region of the phase diagram. For instance, it may go from compressed solid to different phases like hot dense liquid,hot dense plasma, liquid-vapor regime or quasi gas states. As a consequence,the resulting high pressure,energy,and temperature information covers a broad range of the phase diagram.But, in principle, this information has a heterogeneous character which is not complete from the thermodynamic point of view. Its generalization can be done only in the form of a thermodynamically complete EOS.

10. Summary and conclusion

In this paper the effect of radiation environment on shock Hugoniot calculation is investigated by using an improved screened hydrogenic model with l-splitting for electronic contributions to EOS.The ionic contribution to EOS is formulated by Cowan model while cold part calculations are developed on the basis of scaled binding energy model. The results of shock Hugoniot calculations for pressure,energy,temperature with and without radiation field consideration are presented for sodium and iron in this research. The Hugoniot calculations shows compression ratios of 4 for the case without radiation field EOS and compression ratios of 7 with EOS having radiation field included. The results are discussed owing to radiation pressure and free electron pressure. The specific heat at constant volume along shock Hugoniot without radiation field is also carried out in this research that shows Schottky anomaly effect. The results are compared with the published literature and found a very good qualitative and quantitative agreement.