中观观念下的结构化教学主张

陈学军 金鹏

摘  要：依据《普通高中数学课程标准（2017年版）》整体把握教学内容的要求，提出了教学内容结构化分析、学生学习基础结构化分析、教学任务结构化分析、基于知识构成的结构化教学实施等主张，并结合案例进行了诠释.

关键词：整体联系;结构化;学科观念;核心素养

《普通高中数学课程标准（2017年版）》（以下简称《标准》）强调要突出数学的整体联系，关注同一主线、不同主线内容间的逻辑关系，使学生的学习过程成为一个在数学方法、思想指导下的具有系统性、连贯性的有机整体. 章建跃先生也多次指出，数学课程设计中，一定要把建立一个合理的逻辑结构体系作为首要任务.

中观观念下的结构化教学主张就是在数学课程目标的指导下，不仅仅关注当堂课学习的认知过程，而是从整体发展的规律和角度，以及学科知识的构成搭建整体联系的学习支架，把科学形态的数学知识（主要是事实性知识、概念性知识）加工成体现思想方法、数学价值的数学教育形态的知识. 通过对数学内容的整合与开发，使目标、知识、任务、活动形成一个相互一致的整体，在学生认知的最近发展区内纵向连接数学核心内容与数学方法、思想，横向凝聚数学学科核心素养，引导学生在背景和过程中主动探究、构建认识结构，积累获取知识的经验，应用和内化数学思想方法，形成在问题解决过程中以理解数学学习内容本质为指向的心理特征，并培育其后继发展所需要的必备品格和关键能力.

一、教学内容结构化分析

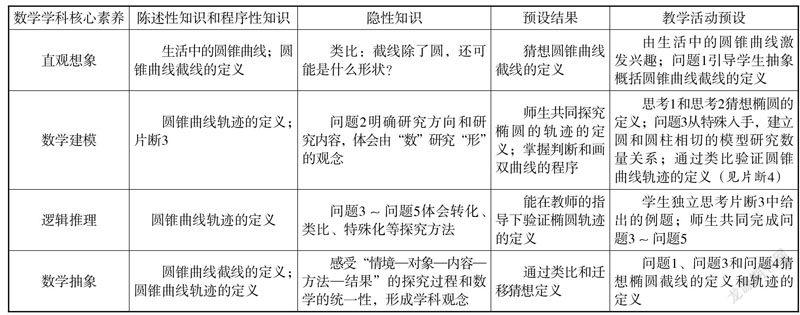
1. 把握教材中学科知识的构成

教材是学科知识的重要载体，决定着教师教什么，学生学什么. 教材中的学科知识由陈述性知识（事实性知识、概念性知识）、程序性知识、方法性知识和价值性知识构成. 其中，陈述性知识、程序性知识是以一定的逻辑结构来表征的，是学科知识的骨架. 而方法性知识和价值性知识是隐性的知识，是学科观念和灵魂. 对于不同的知识，教学策略不同，只有挖掘教材中的隐性知识，洞察到事实性知识、概念性知识和程序性知识背后的过程与方法，以及情感、态度与价值观，才能激活知识与技能，逐渐形成学科素养. “圆锥曲线”的定义为概念性知识，而研究圆锥曲线的一般步骤、判断曲线的形状，以及求其方程则是程序性知识. 如何从实际背景中抽象出圆锥曲线的定义，建立以“数”研究“形”的探究框架，以及对圆锥曲线方程、性质的学习展望，这些关于如何学的策略需要数学的观念方法等隐性知识的支撑.

2. 理清知识产生的背景、联系点和发展点

圆锥曲线有着丰富的实际背景，是刻画现实世界的重要数学模型.

从联系的角度来看：在知识层面上，学生在高中学习物理课程中的开普勒行星运动第一定律时接触过椭圆，而初中所学的二次函数的图象是抛物线;在方法层面上，学生在必修阶段“平面解析几何初步”的学习中已经经历了圆的方程的探究，初步了解了用代数方法研究曲线的基本步骤，而圆锥曲线又是“平面解析几何初步”学习的延续和拓展，是用代数方法研究几何性质、解决几何问题，进一步理解解析几何思想的一个重要载体.

从发展的角度来看，作为章起始课，既要让学生体会到研究圆锥曲线的重要性，引导学生进一步认识到数学的应用价值（为什么研究），又要通过经历从实际背景中抽象出圆锥曲线的截线定义，再从截线定义中挖掘其本质特征，概括出圆锥曲线的轨迹定义，进一步体会数学研究的过程（研究什么），通过搭建研究框架，让学生了解用轨迹定义研究圆锥曲线的必要性，体会用转化、类比、特殊化的方法研究圆锥曲线的一般步骤（怎么研究），培养学生的直观想象、数学抽象、逻辑推理和数学建模能力，为后续的学习奠定基础.

3. 了解数学发展的历史

从文化的角度分析和理解教材是立德树人的根本要求，也是增强学生理性精神的重要途径. 教学中，通过介绍阿波罗尼奥斯的《圆锥曲线论》，以及在笛卡儿创立坐标系之后，比利时数学家旦德林的贡献，揭示了三种圆锥曲线的内在联系，让学生感受数学内在的和谐统一，提升数学审美意识. 引导学生站在前人的肩膀上进行探究，有助于激发学生的学习兴趣，体会到数学的传承与发展，以及不断发现问题、解决问题的艰辛历程.

二、学生学习基础结构化分析

教师站在学生的角度思考：教材给出的起点与终点之间的支架是否合适？是否低估或者超越了学生的生活和经验？教学中，教师常常要从整体出发对教材进行二次开发，使教材中的数学知识结构与学生的数学学习认知结构相匹配.

1. 知识基础

此前学生已经对圆锥曲线有了零散的认识，尤其对椭圆和抛物线较为熟悉，学生在学习高中物理课程的开普勒行星运动第一定律时已经了解了拉线法画椭圆的作图过程，在初中课程中也学习了抛物线的解析式及图象，但是对抛物线的轨迹定义还不太熟悉. 尽管如此，学生对椭圆、双曲线、抛物线的学习还是零散的、相互隔离的. 教学中，教师既要帮助学生激活已有的知识、经验，又要将其已有的知识、经验纳入新的系统当中，促使学生从整体上认识三种圆锥曲线的内在联系，体会学科的一般观念，形成良好的认知结构.

2. 認知障碍

《标准》要求学生了解圆锥曲线的背景与应用，结合情境清晰地描述图形的几何特征. 事实上，从圆锥曲线的截线定义过渡到轨迹定义是实现由“数”研究“形”的关键，需要将立体问题转化为平面问题. 其中，综合了立体几何与平面几何的知识及求动点轨迹的方法，对学生的空间想象能力和转化能力要求比较高，是学生活动探究中的障碍点.

3. 认知冲突

本节课可以从两个方面来设置认知冲突. 一是定性（形）转化为定量（数）：在圆锥曲线的截线定义的形成过程中，由平面截圆锥面直观定性地认识到椭圆、双曲线、抛物线的“形象”，转化为定量地用截面与圆锥面的轴所成角的变化范围来刻画截线的形状. 二是由空间形状到平面图形的认知冲突：在从圆锥曲线的截线定义转化为轨迹定义的过程中，需要将空间的形状转化为描述平面图形的几何特征，这是学生迫切想要探究解决的一个难题.

4. 学习、生活经验

新课程强调数学与生活及其他学科的联系，要求学生从生活视角进行梳理，在数学学科知识发生、发展、形成和应用的过程中，体会数学研究的套路，发展学科观念. 学生学习了直线和圆的相关知识以后，已经有了建立坐标系研究曲线方程和性质的经验，物理学习、生活当中也常能见到椭圆. 例如，斜放着的圆柱形饮料瓶的水面、太阳光斜照篮球的影子轮廓等. 这些生活经验和跨学科的知识及直线和圆的研究经历都是研究圆锥曲线的基础.

三、教学任务结构化分析

在分析《标准》、教材内容及学情的基础上，根据本节课的知识构成，背后隐含的科学观点、方法、价值观，以及与数学学科核心素养的关联，设计任务情境如下表所示.

在此基础上，确定本节课的教学目标如下.

（1）了解圆锥曲线的实际背景，感受圆锥曲线在刻画现实世界时的作用.

（2）通过用平面截圆锥面，经历从具体情境中抽象出椭圆、双曲线、抛物线模型（截线定义）的过程，提升学生的直观想象、数学抽象素养.

（3）经历圆锥曲线轨迹定义的形成过程，从整体上认识三种圆锥曲线的内在关系，初步具备归纳总结、类比、逻辑推理和数学建模能力，通过起始课的学习，在由“数”研究“形”观念的引导下，体会“为什么研究，研究什么，怎么研究”的数学探究一般途径.

（4）通过创设问题情境，激发学生学习圆锥曲线的兴趣，数学史的介绍揭示了圆锥曲线的内在联系，让学生感受数学内在的和谐统一，提升他们的数学审美意识和理性思维.

结构化的教学任务框架，进一步准确地把握教学的起点和归宿，规定了教与学的进程和方向，将知识、活动、目标等逻辑化和具体化，引导教学的全过程，确保了教学目标与过程之间的一致性.

四、基于知识构成的结构化教学实施

教学中，为了更好地实现认知思路和核心观念的结构化设计，针对知识类型，通过知识的梳理与整合、数学思维的程序优化、数学学科观念的建构，提升学生的知识结构化水平，发展学生的数学学科核心素养.

1. 陈述性知识——从知识关联的角度建构教学内容（知识的梳理和整合）

陈述性知识是关于事实及其关系的知识，数学概念和事实是关于“是什么”的陈述性知识. 教学中在分散、孤立的数学事实间建立起逻辑关联的概念，使教学内容结构化，可以更好地引导学生用整体联系的观念理解概念，建构知识体系.

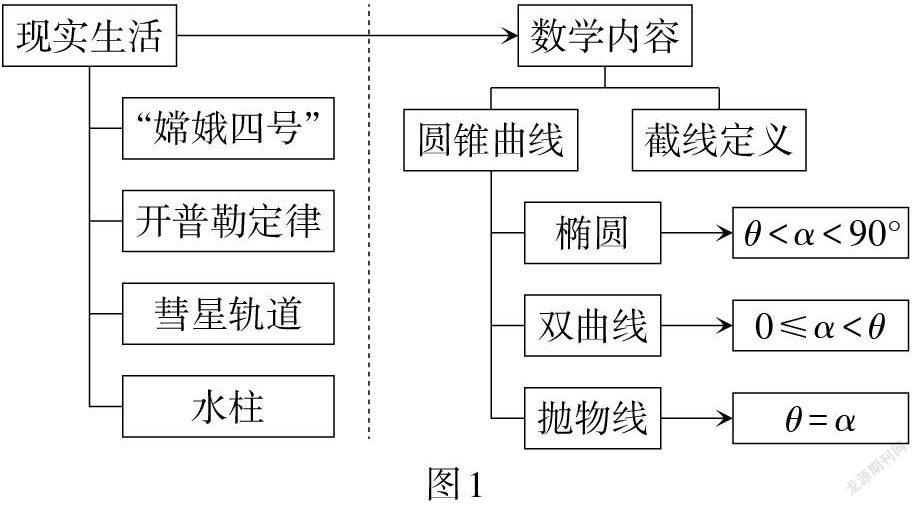
片断1：创设情境，提出问题.（事实性知识：生活中的圆锥曲线.）

师：近几年我国科技进步迅速. 2019年“嫦娥四号”探测器成为第一个在月球背面着陆的人造航天器.

教师播放视频.

师：视频中提到了“嫦娥四号”的运行轨道是椭圆，什么是椭圆呢？

情境1：开普勒行星运动第一定律：太阳系中的每个行星都在某个椭圆上运动，这些椭圆都以太阳为一个焦点.

情境2：彗星的运行轨道有些是椭圆，有些是抛物线，有些是双曲线.

情境3：喷水池中的水柱都呈抛物线形.

椭圆、双曲线和抛物线统称为圆锥曲线.

片断2：如何用数学语言刻画圆锥曲线？（概念性知识：圆锥曲线的截线定义.）

问题1：我们知道平行于圆锥底面的截面的截线是圆. 改变截面的位置，截线会变成什么形状？设圆锥面的轴与母线所成的角为[θ]，不过顶点的截面与轴所成的角为[α].

生：[α=90°]时，截线是圆. 截面的位置变化时，截线的形状可能是椭圆、双曲线和抛物线.

教师板书图1.

教学中，从学生头脑中零散的关于圆锥曲线的直观形象入手，通过圆锥面的截面，得到圆锥曲线的截线定义，建立了三类圆锥曲线之间的联系（图1），引导学生用数学眼光观察世界，增强学生的抽象和概括能力.

2. 程序性知识——从认识思路的角度建构数学内容（活动操作的流程）

程序性知识是关于完成某项任务的行为或措施步骤的知识. 数学中的运算、解决问题的探索步骤、解决的方法及操作流程等都是关于“如何做”的程序性知识.

片断3：教师给出一道例题.

如图2，取一条拉链，打开它的一部分，在拉开的两边上各选择一点，分别固定在点[F1，F2]处，随着拉链逐渐拉开或者闭拢，笔尖所经过的点就画出一条曲线，这条曲线是双曲线的一支，试说明理由. 如果想再画出双曲线的另一支，怎么操作？

画出双曲线另一支的操作和依据：拉链两边各取一点[数学化]固定在[F1，F2]处[→][MF2-MF1=定值]（小于[F1F2]）[操作]双曲线的另一支.

在帮助学生理解题意的基础上，搭建认知思路层面上的程序性支架，可以引导学生用数学的思维系统缜密地分析问题，规范、高效地解决问题，提高逻辑推理能力.

3. 策略性知识——从学科觀念的角度建构教学内容（方法与思维认知的建模）

策略性知识指如何学习和思维的知识，是对如何进行问题探究、观念建构与“一般套路”的思维模式的认知. 教学中，将数学知识的建构、数学方法的运用、数学思维的训练等“如何学”的统摄性知识融入核心知识的教学内容中，可进一步优化学习策略，提升学生的关键能力.

片断4：圆锥曲线的轨迹定义.（策略性知识：构建研究过程的认知.）

问题2：有了圆锥曲线的截线定义，接下来我们该研究什么？怎么研究？

这是本节课研究的核心问题，也是关于如何学习的问题.

生1：接下来应该研究性质，像研究圆一样，通过建立平面直角坐标系，用代数的方法进行研究.

生2：这个空间图形好像很难建立平面直角坐标系，我们也不知道曲线上的点满足什么条件，怎么建立方程？

生3：关键要知道曲线上的点满足的条件是什么.

师：对，要用代数方法来研究圆锥曲线的性质就必须研究其轨迹定义，我们还是从熟悉的角度入手.

思考1：绳子的一个端固定在平整的草地上，另一端拴着一只小羊，小羊活动的最大边界是什么曲线？

生1：圆，圆上任意一点[M]满足[MO=]绳长（定值）.

思考2：绳子两端固定在平整的草地上（绳长大于两固定点间的距离），绳上套一个小环，环上拴一只小羊，小羊活动的最大边界是什么曲线？学生可以在纸上试着画画看.

生2：椭圆. 猜想，满足[MF1+MF2=]绳长（定值）点的轨迹为椭圆.

師：这里小羊的最大活动边界为什么是椭圆呢？

思考2建立在圆的轨迹定义学习经验的基础上，学生通过亲手实践，类比、猜想得出椭圆的轨迹定义，并试图精确刻画，这时与已有截面定义产生思维碰撞，激发学生的求知欲.

生3：这两个定义是一致的吗？

师：要回答生3的问题，还是从生活当中熟悉的、特殊的情况入手.

问题3：大家知道水平地面上太阳光斜照下的篮球影子的轮廓是椭圆，如图3所示. 如果把与球相切的光线看成是一个圆柱面，地面看成截面，在椭圆上任意取一点[M]，点[M]与哪些量有关？

生1：设球与地面的切点为[F1]，过点[M]的圆柱的母线与球面的切点为[Q]，则有[MF1=MQ]，如图4所示.

师：还有其他等量关系吗？学生展开讨论.

生2：由思考2，联想到椭圆和两个量有关. 逆过来，如果光线从地面下方沿相反的方向照过来，地面下方大小相同的球的影子也是这个椭圆，如图5所示. 设地面下方的球与地面的切点为[F2]，延长[QM]到点[R]. 类似地，也有[MR=MF2]，如图6所示. 因此，[MF1+][MF2=QR]（定值）.

问题4：把圆柱的一个面缩成一个点，能否类似地得到[MF1+MF2=QR]（定值）？

问题5：你能类似地研究双曲线的轨迹定义吗？

师：根据刚才的研究，怎样完善图2的结构？

师生共同活动，构建了本节课的学习活动导图，如图7所示.

片断4围绕如何用代数的方法研究圆锥曲线这个目标，用类比的方法，将椭圆的空间截线定义转化为研究平面的轨迹定义，方法层面从具体、熟悉、特殊的和已有经验入手逐步进行探究，进而得到结论. 在引导学生用数学语言表达数量关系的活动中经历了揭示背景、提出问题、明确方法、假设猜想、验证确认、实践运用的探究过程，增强了学生的学科观念，提升了他们的数学建模意识和理性精神.

作为章起始课，在结构化的教学主张中注重概念的联系和统一，突出研究思路的剖析，形成认知程序，体会研究方法和研究结论的类比. 帮助学生在更高、更宽的视野下理解知识的背景和生长点，准确把握核心概念之间的逻辑关联、体会知识背后所隐含的科学方法和理性思维，逐步提升数学学科核心素养.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2]章建跃. 发挥数学的内在力量为学生谋取长期利益[J]. 数学通报，2013，52（2）：3-6.

[3]季苹. 教什么知识：对教学的知识论基础的认识[M]. 北京：教育科学出版社，2009.