云机器人系统的计算卸载策略研究
孙 弋, 许志杰
(西安科技大学 通信与信息工程学院, 陕西 西安 710054)
近年来伴随着嵌入式系统性能的提升、传感器技术的蓬勃发展[1]以及移动数字网络技术的快速迭代,全球范围内,应用机器人市场规模增长明显[2]。不同于执行特定程序的物理设备,机器人具有高度的自主决策能力,对不同环境和场景适应性强,且机器人群组之间的协作愈发成熟[3]。如何实现机器人集群的大规模应用以及使机器人在有限功耗的限制下,具备强大的计算能力和低廉的部署成本成为亟需解决的热点需求。基于网络技术将机器人本体需完成的数据分析与处理、行为决策与规划、机器人群组协同等复杂的计算任务卸载到云端执行,通过数据共享,凭借云端专有的软硬件资源代替机器人执行更加复杂的计算任务、存储更大规模数据、为机器人提供服务的系统称为云机器人系统架构。郭宇[1]利用连通支配集对云机器人底层网络建模,并结合能耗敏感模型实现对整个机器人自组织网络中的能量和时间延迟进行分析,并在该模型下设计了基于遗传算法的计算卸载策略。博弈论是研究分布式多智能体系统中决策者之间相互作用关系的数学工具,而云机器人系统作为典型的分布式系统,其服务的提供者与使用者,及使用者与使用者之间的博弈时刻存在,其中边缘云拥有对计算资源的定价权,是博弈的领导者,而云机器人依据自身情况及所需资源价格做出卸载决策,是博弈的跟随者。Xu等[4]对云机器人系统中的任务进行分割与建模,基于多边缘网络中云机器人计算卸载问题设计了改进的博弈论算法,提高机器人网络服务质量和用户体验。尤斐然[5]应用博弈论设计资源优化分配的策略,分析一对多、多对对、多层联合博弈的模型下的资源分配效率。上述文献从博弈论的角度对资源分配与能耗进行分析,但未讨论博弈各方决策时的相互影响。针对上述不足,本文将多个机器人终端竞争同一边缘云服务器中相同类型资源或服务的行为建模为Stackelberg博弈模型,基于逆向归纳法求解在多阶段博弈过程中边缘云与机器人终端的决策问题,求得云机器人系统博弈中双方策略最优的Nash均衡解,实现双方效用函数的最大化。
1 相关研究
1.1 云机器人系统架构
云机器人系统是在传统的分布式网络机器人系统之上,结合云计算[6]服务发展而来的一种新兴发展方向。这一概念在2010年由Kuffner教授[7]首次提出,旨在利用互联网大规模并行计算和近乎无限的分布式存储能力为机器人设计统一的服务交互模型,扩展其计算能力以及增强其服务能力。根据服务提供方式的不同,将该模型分为面向服务(SOA)的平台架构和提供机器人即服务(RaaS)的平台架构[8]。Arumugam等[9]基于平台即服务的思想,设计DAvinCi的云机器人计算框架,并采用Map/Reduce的方式实现了机器人同步定位与地图构建算法的云服务平台。Quintas等[10]提出了面向服务的机器人系统,其中机器人和智能空间共享知识。Du等[11]基于机器人即服务提出了机器人云中心(robot cloud center)的框架,其结合了SOA架构和云计算模型,使任务以最大效率,耗费最少资源完成。结合相关研究背景及云计算的特点,本文拟将机器人任务封装为众多独立微服务,构建RaaS的云机器人服务管理系统,机器人通过端到云的网络向云端请求所需计算服务。计算卸载策略是云机器人进行计算卸载的关键,其决定任务是否进行卸载以及卸载数量。
1.2 计算卸载
计算卸载[12-13]是解决边缘计算中用户终端设备在计算和存储资源等方面的不足,是云机器人架构最重要的特点之一。用户终端将对时间延迟不敏感的计算密集型任务迁移到专用服务器上运算,待计算完成后接收计算结果的过程称为计算卸载,其流程见图1。
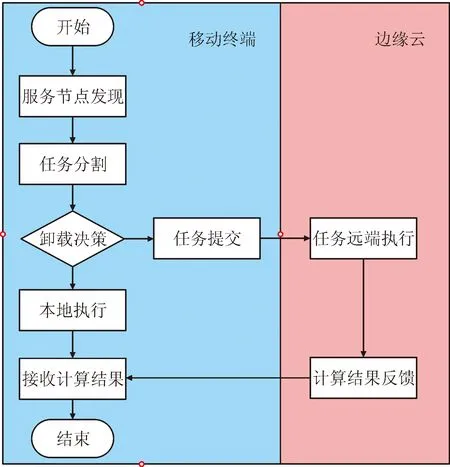
图1 计算卸载流程图Fig.1 Calculation offloading flow chart
计算卸载分二进制卸载和部分卸载两种方式。二进制卸载方式指计算任务不可分割,其程序和数据作为统一整体卸载到边缘云执行,由此其对通信网络的传输能力、网络延迟提出了较高的要求,服务作为整体卸载到边缘云端,降低了云端资源调度策略的设计难度,但使请求服务调度失效时的异常处理难度增加。Chen等[14]研究在任务执行时延和能耗约束下,多参与者通过非合作博弈达到最优计算策略的二进制卸载问题。Ma等[15]研究无线网络组网环境中多用户终端的计算卸载问题,结合博弈论将所有用户的计算任务,无线频带分配和计算资源进行建模,获得使任务执行成本最小的最优策略。Chen等[16]也是利用非合作博弈模型分析多用户终端之间卸载策略的相互影响,基于降低任务执行总代价和时间延迟,获得最优的计算卸载策略使通信与计算资源分配最优。部分卸载方式指将计算任务分割为多个子任务,一部分在本地执行,一部分在边缘云执行,既减少计算任务传输数据总量,又提高子任务执行的并行性,充分发挥本地和边缘侧协同计算的优势,提高任务执行的效率,同时需为到达边缘侧的子任务设计任务调度机制,满足依赖关系的子任务串行执行,相互独立的子任务并行执行。Dai等[17]基于多边缘云服务器之间的负载均衡问题,在满足任务执行时间和能耗的条件下设计使系统整体耗能最小的最优卸载策略。Jie等[18]将移动边缘计算环境中用户之间的计算卸载策略抽象为符合主从关系的Stackelberg博弈,为优化任务的响应时间和资源利用率设计了一种任务调度算法。You等[19]研究在同一网络中只有单一边缘云服务器时,多终端设备将部分任务卸载到边缘云中执行时所需的信道资源分配问题,优化任务执行所需时间。上述文献均假设边缘云服务器拥有无限的计算资源,而云机器人系统在现实的计算平台中运行,其次对选择部分卸载时结合能耗和时间延迟的计算卸载系统研究不足。
综上,为降低通信设备压力,提高云端服务调度灵活性,本文在云机器人系统中选择部分卸载的计算卸载策略。本文重点研究在同一边缘“网络”只有单个边缘云,且边缘云的计算资源是有限时,实现机器人计算任务部分卸载的策略研究。
2 计算卸载系统模型
云机器人系统中的计算卸载是典型的边缘计算(MEC)问题,根据上述对计算卸载的介绍,结合云机器人计算任务本身的特点可知:1)云机器人中的部分任务只能在本地执行,且存在云端资源竞争不足等情况,故采用动态部分卸载的策略;2)云机器人中的计算任务可被分割,部分在本地执行,同时其他部分被卸载至边缘服务器执行,根据计算卸载的影响因素决定单节点卸载还是多节点卸载。本文的博弈论算法是研究多个机器人竞争同一边缘云服务器资源,欲将计算任务卸载到边缘服务器中执行以减少自身设备的计算成本。任何一个机器人的卸载决策都会影响同一边缘“网络”中其他机器人终端的计算卸载决策。在云机器人系统的计算卸载模型中,处于同一边缘“网络”中的节点大多只有一个,符合多对一的模型。下面就基于Stackelberg博弈论的计算卸载策略方法进行论述。
2.1 系统网络模型
一个计算卸载网络由一个具备计算加速服务的边缘云和K个机器人终端集合N={1,2,…,K}组成,单个通信AP节点下管理至多K个移动机器人终端,其网络模型见图2。
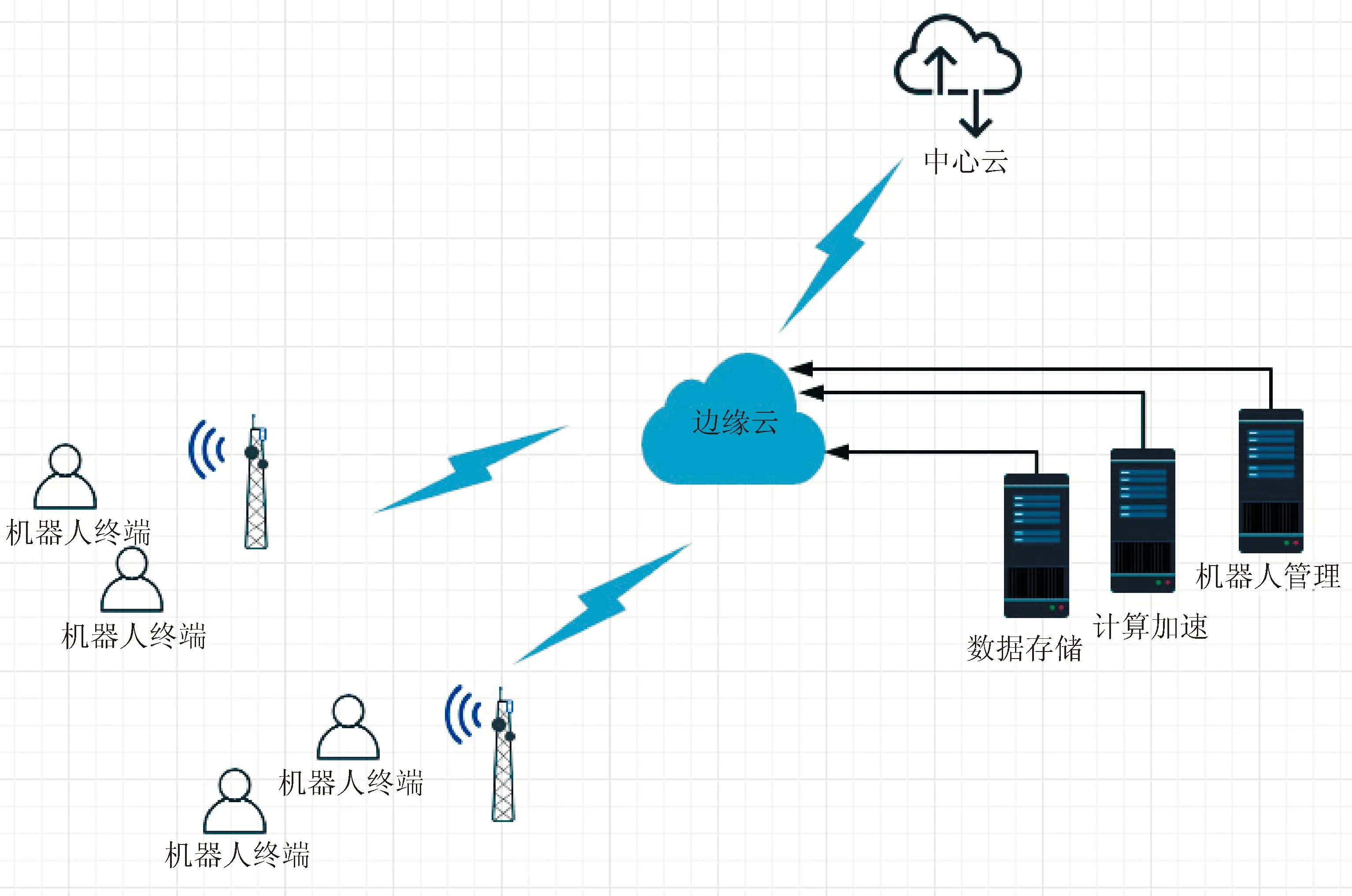
图2 系统网络模型Fig.2 System network model
计算卸载方式为动态部分卸载,即机器人终端任务可按功能拆分为多个大小各异的简单任务,一部分在本地执行,另一部分在边缘服务器上执行。边缘云计算平台与通信AP节点之间采用有线网络,不考虑在有线传输过程中所产生的通信损耗和时间延迟,通信AP节点通过无线网络与机器人终端进行连接,该无线网络可分配的总带宽为B。假设每个机器人终端与通信AP节点之间的信道相互独立,互不干扰,每个机器人可均匀分得的最大带宽为B/K,且通信能力不随该节点管理机器人数量增加而下降。随着机器人终端的移动,其与通信AP节点之间的信道会随着位置发生改变,假设单次任务卸载周期内信道环境参数保持不变,但不同卸载周期信道环境参数可能改变。
2.2 任务执行模型
基于上述的网络模型,计算任务可在本地或边缘侧执行,首先对计算任务进行建模。云机器人系统中,功能各异的机器人终端选择适当的CPU计算能力,编号为k的机器人终端其计算能力用每秒CPU周期数Fk衡量,单位为cycles/s,执行任务所需计算数据总量为Rk,单位为Byte,每执行1bit数据所需的CPU周期数为Ck,单位为cycle。计算任务卸载到边缘侧执行的比例为xk,0≤xk≤1,故执行卸载的数据量为xkRk,本地执行的数据量为(1-xk)Rk。时间延迟和能量消耗是评价计算卸载策略优劣的重要指标,下文对任务本地执行和任务远端执行中的时间延迟和能量消耗计算方法进行建模。
1) 任务本地执行模型
任务在本地执行计算过程中所耗费的时间和能量即时间延迟和能耗。计算能力为Fk的机器人终端执行数据量大小为(1-xk)Rk的计算任务所消耗的时间和能量分别为:
(1)
(2)
式中:Vk表示每CPU周期消耗能量,单位J。
2) 任务远端执行模型
(3)
(4)
机器人终端与通信AP节点之间的信道带宽为B/K,单次计算卸载周期内信道噪声功率不变,为σ,其本地通信设备发送功率为Pk,机器人终端与通信AP节点之间的信号增益为Gk,根据Shannon公式可得:
(5)
因此机器人终端k上载任务数据到边缘云上的传输时间为:
(6)
数据的上载和下载处于相同信道环境中,可得数据下载速率为:
(7)
式中:PBS为通信AP节点的通信设备发送功率。
计算结果的数据量相较于输入数据量明显减少,用α表示输出数据量与输入数据量的比值,则反馈到机器人终端的数据量为αxkRk,因此计算结果反馈时间为:
(8)
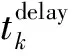
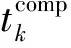
(9)
在此系统中任务可在本地和边缘侧同时进行计算,因此机器人k执行总数据量为Rk的任务需要的时间为:
(10)
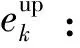
(11)
式中:TPs,k表示机器人k通信设备的发送功率。
计算结果反馈过程中所消耗能量为:
(12)
上式中TPr,k表示机器人k通信设备的接收功率。则可得机器人终端执行计算卸载所消耗的能量为:
(13)
为对计算卸载过程中需付出的代价进行评估,设计了由多项式组成的评价代价函数公式:
(14)
能耗权重因子λe和时间延迟因子λt满足约束条件,λe+λt=1。则计算卸载过程中总的代价函数表示为:
(15)
2.3 云机器人系统中的Stackelberg博弈模型
部署在云机器人系统环境中的边缘云服务器计算资源通常是有限的,且同时服务的用户数也存在上限,因此边缘云与机器人终端之间,每个机器人终端之间都存在着明显的博弈过程,即边缘云通过对服务定价影响机器人终端的卸载决策,而每个机器人终端的卸载决策同时也会对其他机器人的决策产生影响。为激励机器人终端将计算任务卸载到边缘云上执行,保证云机器人系统高效运行的前提下,解决边缘云定价策略与机器人终端卸载策略的平衡问题,给出当前系统条件下的最优价格和计算卸载策略集。
机器人终端的卸载策略集X={x1,x2,…,xK}代表每个机器人卸载数据到边缘云中占总数据量的比例,0 1) 机器人效用函数 机器人终端执行计算卸载过程中的代价包括计算等待时间延迟、传输能耗以及使用边缘云服务支付的费用,可将机器人终端k的成本表示为: (16) 机器人终端k的效用函数由任务执行所得收益与执行总代价之差组成,所得收益可用对数函数表示为Yk(xk),参数β与机器人终端任务相关,β>0。 (17) 则机器人终端k的效用函数表示为: (18) 在给定的边缘云价格策略集下,机器人终端确定计算卸载策略集,最小化自身成本函数P1: (19) 同时期望获得最大的自身效用P2: (20) 式中:tk代表机器人k执行卸载计算的总时延;ek代表机器人k执行卸载计算的总能耗;Tmax代表任务的最大等待延迟;Emax代表最大剩余可用能量。在众多参数的限制下需要最优化机器人终端自身效用。 2) 边缘云效用函数 机器人使用计算资源支付的费用的总和即为边缘云效用函数的表达式: (21) 在满足边缘云最大计算资源的条件下,边缘云调整其定价策略,激励机器人终端卸载任务到边缘云中,最大化自身收益P3: (22) 式中:Fedg_all为边缘云最大的计算资源数。 逆向归纳法通过将多阶段动态博弈过程沿时间轴划分为多次单人博弈,确定每个参与者在不同时间点的最优选择,是分析和求解Stackelberg博弈均衡策略的常用方法。P3问题中制定的价格会影响P1优化问题中的卸载策略,而同样P1问题的卸载策略会反作用于P3问题,问题P1和P3是耦合的。结合逆向归纳法,将机器人终端的卸载策略问题分解为给定边缘云定价策略集下的子问题,通过求解P1问题得到最优卸载策略集,而边缘云服务器可在已得最优卸载策略下解决P3问题中的最优价格。经过多次子问题的演化分析,得到全局最优的卸载策略集和价格策略集。 (23) (24) 将解xk代入机器人终端的成本函数后可得: (25) 在给定价格策略集下,pk视做常数,则上方成本函数可表示为变量xk的分段函数: (26) 可将上述公式简化为: (27) 分析可知,当A1k<0 (28) (29) 当边缘云计算资源定价小于ω1k时,机器人终端将把所有计算任务卸载到边缘云中执行,而此时由于边缘云请求的计算服务量过大,导致其处理任务的效率变低,因此边缘云定价应避开设置在该范围。当边缘云计算资源定价大于ω2k时,机器人终端在进行计算卸载时的成本开销过大,导致所有任务都在本地进行,而边缘云的收益为0,因此边缘云定价应避开此区间。当ω1k≤pk≤ω2k时,机器人终端将部分任务卸载到边缘侧执行,保证了边缘云的收益和任务处理效率,减少机器人处理任务的能耗。 1) 二进制字串的第一个位置若为1,则起始位置为(1,2),否则起始位置为(2,1)。进入子串的下一个位置。 2) 当下一位置上的二进制值为1时,则1被填充到水平方向上的表格中,若下一位置的二进制值为0,则0被填充到垂直方向上的表格中。 例如,在一个机器人终端数为10的云机器人系统环境中,将动态规划填充表使用图3中的一个二维10×10的表格表示。 图3 算法示例Fig.3 Algorithm example 假设第一个随机字串为 “1110011001”(见图3(a)中黑色字串)或者 “0011011000”(见图3(a)中红色字串)。第二个随机字串为 “1100011110”(见图3(b)绿色字串)。因为第二个字串的第一位为1,所以起始位置为(1,2)。基于该方法处理,可有效减少公共子串的重复计算。 每生成一个随机的二进制字串,需要计算该字串总的执行时间和能量消耗,同时还需要计算表格中每个方格的总能量消耗和执行时间。但是如果生成的随机字串与在表格中的字串有相同的部分,则在计算二进制字串的时间和能耗时只计算到第一个相同数值的方格,然后将新计算的总能量和记录在该方格内的总能量相比较。如果新计算的总能量小于记录在方格内的能量,则使用新的子串代替旧的子串,并使用新计算的总能量、能量消耗以及执行时间替换掉已记录的值。基于该规则更新剩下的所有子串的能量和执行时间。否则,如果新计算的总能量大于记录在方格中的总能量,则保留在该方格中已记录的子串。当算法中的字串Hamming距离大于给定阈值,便终止循环并返回计算结果。 机器人终端的CPU处理能力随机分布于集合{0.1 GHz,0.2 GHz,…,1.0 GHz}之中,每执行1字节数据需要消耗的CPU周期数在500~1 500 cycles/bit随机分布,机器人终端k的输入待处理数据总量Rk设置为100~300 KB的随机值。机器人终端通信设备的发射功率为0.1 W,接收功率为0.06 W,通信AP节点的发射功率为1 W。边缘云计算能力100 GHz。机器人数量最小为15,以15的倍数增长。时间权重因子λt随机分布于区间[0,1],能量权重因子λe=1-λt。 在将系统部分参数去除随机性后,机器人终端成本开销和效用随计算卸载比例的变化曲线图见图4和图5。 图4 计算卸载成本均值随卸载比例实验曲线Fig.4 Experiment curve of average offloading cost at offloading ratio 图5 机器人终端效用均值随卸载比例实验曲线Fig.5 Experiment curve of average utility of robot terminal at offloading ratio 随着计算卸载比例增大,更多的计算任务卸载到边缘测执行,使机器人终端计算成本降低。但由于越来越多的机器人对任务执行卸载,使边缘云资源竞争愈发激烈,导致计算资源价格上升,使机器人终端的成本函数增大,因此机器人终端成本开销的平均值会随着卸载比例的增大先减小再增大。而用户效用的平均值会随着卸载比例增大,付出更多的成本,而执行计算卸载的收益趋于平衡。此实验验证了系统模型的正确性。 图6表示当边缘云网络内的机器人终端数量增加时,任务全部本地执行和使用本文提出的Stackelberg博弈方法在机器人终端成本开销上的对比结果。结合文中的分析可知,在使用Stackelberg博弈方法时,机器人终端成本开销的平均值明显低于本地执行的开销,因为虽然本机计算无需向边缘云支付计算资源费用,但本地计算时间延迟较高,使成本开销增大。 图6 机器人终端本地及卸载计算成本随用户数实验曲线Fig.6 Experiment curve of tasks’ cost running in local and offloading follow the growing usrs 本文基于Stackelberg博弈思想设计了云机器人系统环境下机器人终端执行计算任务卸载的优化算法,解决在多机器人终端竞争同一边缘云服务器计算资源场景下的边缘云效用及机器人终端效用均衡问题。并就移动终端的卸载决策问题提出了一种基于动态规划的优化算法,该算法通过开辟存储计算过程的数组,减少了对公共子串的重复计算。通过对不同计算能力和能量状态的机器人终端设置不同的权重因子,以及对计算卸载决策博弈过程的分析,分别选择对机器人终端和边缘云最优的卸载策略和定价策略。结合实验分析,该系统有效降低机器人终端计算能量消耗以及提高边缘云自身效用,并验证了系统模型的正确性。2.4 云机器人系统中Stackelberg博弈求解

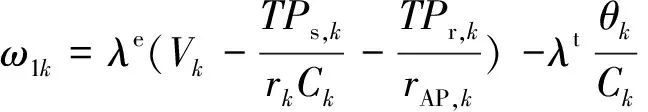
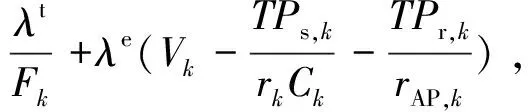
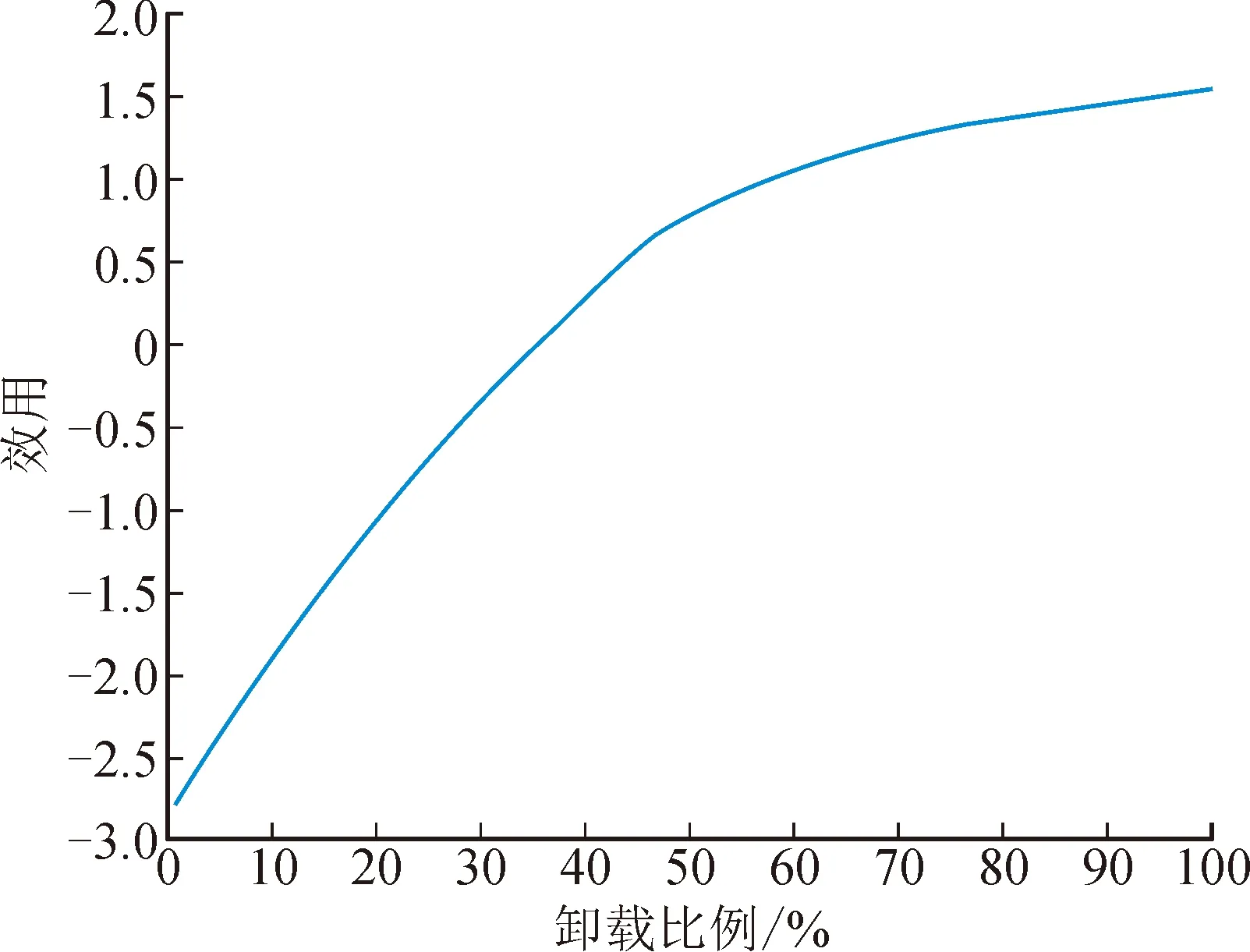
3 系统实现与测试



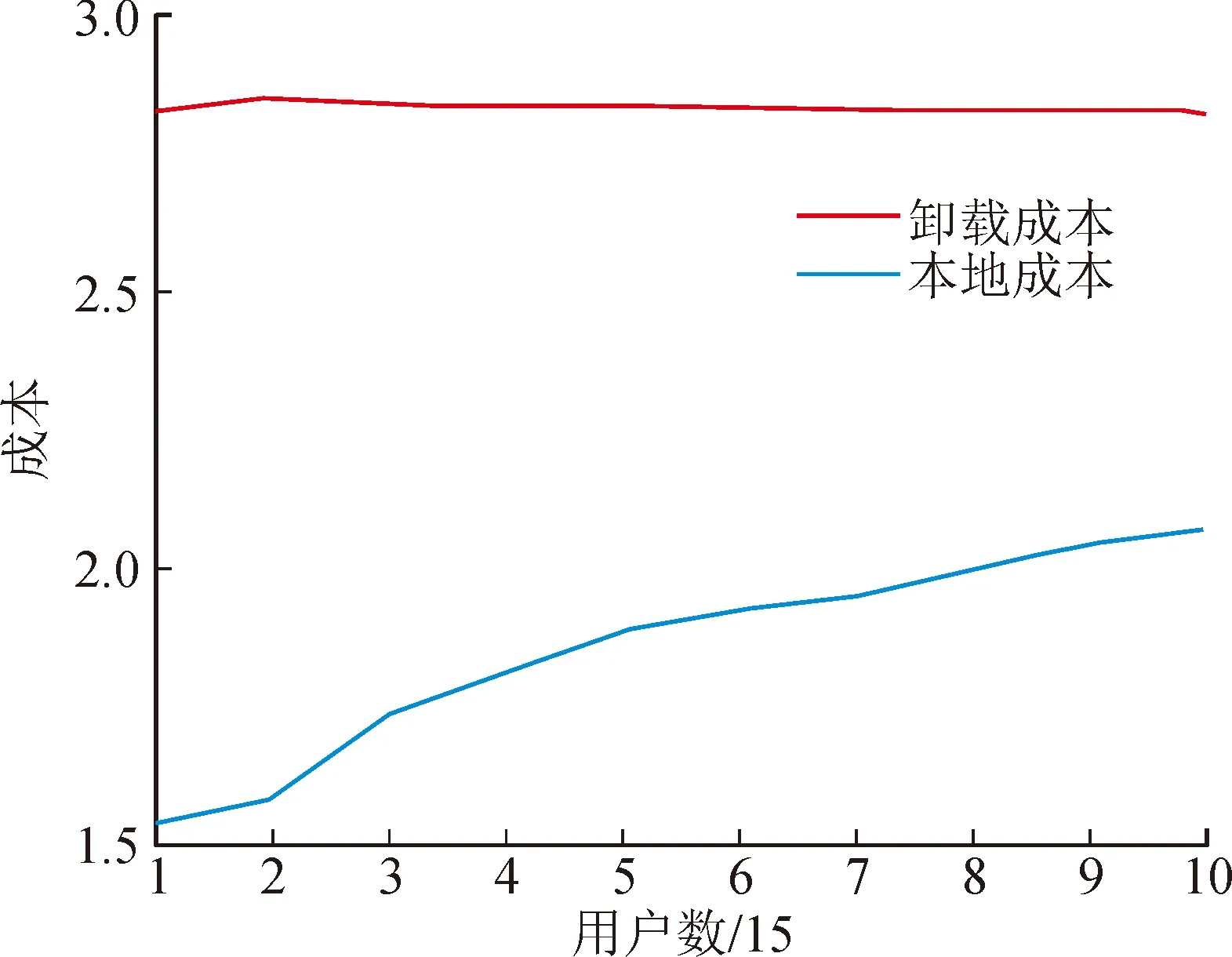
4 结 语

