基于快速平行因子分解的声矢量传感器阵二维DOA 估计

陈未央，徐 乐，张小飞

（南京航空航天大学电子信息工程学院，南京211106）

阵列信号处理中的接收信号波达方向（Direc⁃tion of arrival，DOA）估计，近年来获得了广泛的关注和迅速的发展［1⁃3］，而在水声信号处理中，新型的声矢量传感器也越来越多地被应用到信号参数估计中。声矢量传感器一般由声压传感器和振速传感器组成，相比于传统的信号接收传感器，声矢量传感器可以同时测量空间中某点声场的标量和矢量，即同步共点测量声场中一点处的声压和质点振速若干正交分量，具备较强的抗各向同性噪声干扰的能力［4］，这些特点使得声矢量传感器阵列对于信号参数估计具有较大优势。

近年来，学者们已相继提出了许多关于声矢量传 感 器 阵 列DOA 估 计 的 算 法［5⁃11］，包 括 多 重 分 类（Multiple signal classification，MUSIC）算法［5⁃6］、借助旋转不变性进行信号参数估计（Estimation of signal parameters via rotational invariance tech⁃nique，ESPRIT）算 法［7⁃8］、传 播 算 子（Propagator method，PM）［9］，以及最大似然（Maximum likeli⁃hood，ML）算法［10］等。其中，基于子空间类的方法，如MUSIC 算法和ESPRIT 算法，通常要对接收信号协方差矩阵进行特征值分解，其计算复杂度较高。而PM 算法利用传播算子矩阵获得信号的参数估计，避免了接收信号协方差矩阵分解过程，其复杂度较低，但在低信噪比的情况下，该算法参数估计性能较差。

平行因子（Parallel factor，PARAFAC）模型最早于生理学中提出，用于对多维数据分析［12⁃13］，近年来，该技术被成功地运用到了信号处理领域。文献［14］利用平行因子模型中的PARAFAC 分解方法，能够得到声矢量传感器阵列二维DOA 估计。然而传统PARAFAC 算法直接利用随机矩阵进行初始化，如采用高斯随机矩阵初始化，后进行循环迭代更新，直到分解收敛。但该过程所需收敛次数较多，迭代分解过程收敛较慢，导致算法计算复杂度很高，特别是在阵列阵元数较大或信号采样快拍数较大的情况下。

为了降低平行因子方法的复杂度，本文提出了一种适合任意矢量传感器阵列结构的基于快速PARAFAC 分解的二维DOA 估计算法。该算法首先将接收信号构建为平行因子模型，然后在数据域对该模型中的参数矩阵进行初始估计，最后利用三线性交替最小二乘（Trilinear alternating least square，TALS）算法［15⁃16］得到和信号一一匹配的仰角和方位角估计。所提算法基于减少迭代分解的次数、加快收敛速度的思想，对传统平行因子方法改进，对所构建的平行因子模型中的参数矩阵进行了初始化估计，大大加快了PARAFAC 分解的迭代过程。与普通的PARAFAC 算法相比，该算法复杂度较低。同时，其二维DOA 估计性能非常接近于PARAFAC 算法，同时优于ESPRIT 算法和PM 算法。

1 数据模型

假设有K 个远场信号被阵列所接收，其中信源数K 已知，阵列由M 个任意分布在三维空间中的声矢量传感器组成，其结构如图1 所示。

图1 信号接收阵列结构图Fig.1 Structure of signal receiving array

假设阵列所接收的信号均为非相干的窄带信号，所含噪声均为加性高斯白噪声，且与信号独立［14］。第k 个信号的波达方向为(φk，θk)，其中φk为信号方位角，θk为信号仰角。则阵列中第m 个阵元在t 时刻的接收信号可以表示为［14］

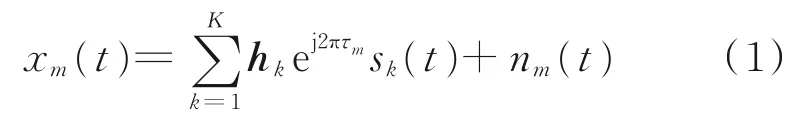
式中：sk(t)为第k 个信源的传输信号；τm为相较于参考阵元，信号到达第m 个传感器的时延；nm(t)为接收噪声；hk为第k 个信源的方位矢量，表示信号在各个方向上的正交分量，可写为［4］

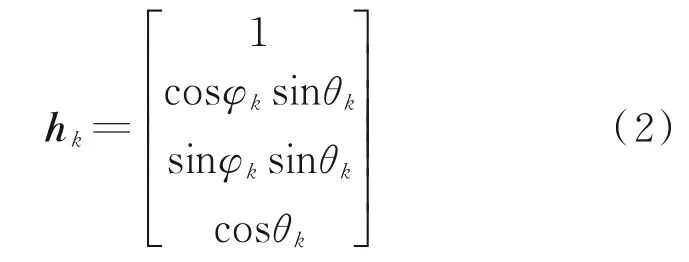
整个阵列在t 时刻的接收信号可以写为［14］

式中：“∘”表示矩阵的Khatri⁃Rao 积；A∈CM×K为整个阵列的方向矩阵［14］；s(t)=[s1(t)，s2(t)，…，sK(t)]T为信源矢量；H =[h1，h2，…，hK]∈C4×K。则阵列J个快拍的接收信号可以表示为

式中：Dm(·)表示取矩阵的第m 行组成的对角阵，SJ×K=[s(t1)，…，s(tJ)]T为 信 源 矩 阵；Nx=[n(t1)，…，n(tJ)]为J 个 快 拍 的 信 号 噪 声；Xm=HDm(A)ST+Nxm(m=1，2，…，M )，其 中Nxm为切片噪声。Xm可以表示成平行因子三线性模型［15］，即有

式中：am，k和hp，k分别为矩阵A 和H 的第（m，k）和（p，k）元素，sj，k为S 的第（j，k）元素，nm，p，j为噪声切片Nxm的 第（p，j）元 素；m=1，2，…，M；p=1，2，3，4；j=1，2，…，J。该结构还可以写成另外两种表达形式［14］

式中Ny和Nz为变换后相应的噪声。

2 二维DOA 估计算法

普通的PARAFAC算法通常直接利用三线性交替最小二乘算法对该模型进行分解。但该迭代分解过程收敛较慢，导致PARAFAC 算法计算复杂度较高。为了加快接收信号模型分解收敛速度，本文算法先在数据域对模型中的参数矩阵进行初估计，然后再利用PARAFAC分解得到信号的二维DOA估计。

2.1 参数矩阵初估计

式（4）中的接收信号，经过初等行变换可以表示为

式中：N′为变换后相应的噪声；G ∈C4M×4M为行变换矩阵，表示为

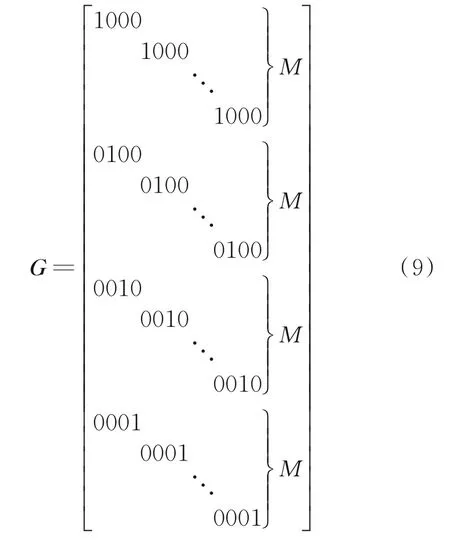
定义B=H ∘A，对矩阵B 进行分块

式中：B1∈CK×K；B2∈C(4M-K)×K。则存在一个矩阵P ∈CK×(4M-K)满足［9］

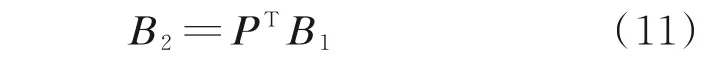
接收信号的协方差矩阵为

对R 进行分块得到

式中：R1∈C4M×K；R2∈C4M×(4M-K)。在无噪声情况下R1和R2满 足

可以通过求解下式的最小值来获得矩阵P 的估计［9］

式中‖ · ‖F表 示矩阵 的Frobenius 范数，通过 式（16）可以求得P 的估计为

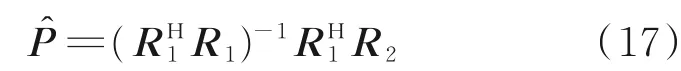
得到P̂的估计后，可以得到矩阵P̂c=[ IK×K，P̂]T。对P̂c进行分块

式 中P1、P2、P3和P4均 为M ×K 的 矩 阵。则 根 据PcB1=B 以及B=H ∘A，有

根据式（19，20）可以得到P2B1=P1B1D2(H )，然后可得

式中：(·)†表示矩阵广义逆，对P†1P2进行特征值分解，其特征值即为D2(H )的估计值D2(Ĥ)。同时，可 以 得 到B1的 估 计 值B̂1，进 而 可 得B 的 估 计B̂=P̂cB̂1。将B̂进行分块可以得到

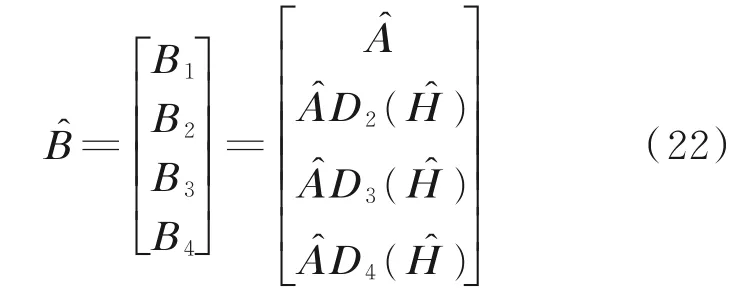
式 中B1、B2、B3和B4均 为M ×K 的 矩 阵。由 式（22）即可得到矩阵A 的初始估计Âini=B1。同时可以得到B3=B1D3(H )，B4=B1D4(H )，然后可以得到D3(H )和D4(H )的估计为

至此，已经获得了矩阵A 的估计Âini。同时，D2(Ĥ)、D3(H )和D4(H )的对角元素即分别为矩阵H 第2、3、4 行的估计，由于H 第1 行全部由元素1 组成，因此最终也可获得H 的初始估计Ĥini。

2.2 三线性分解与二维DOA 估计

三线性交替最小二乘算法是平行因子模型中常用的分解方法，该算法每次更新模型中的一个矩阵的估计，直到收敛。

通过式（4）可以得到最小二乘拟合为［14］

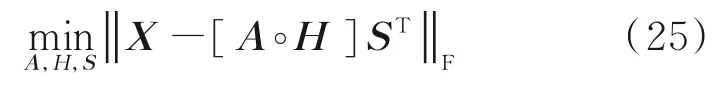
由式（25）可以得到S 的估计为

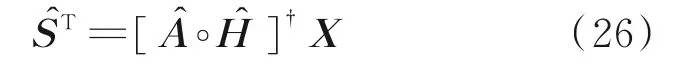
式中Â和Ĥ为上一次迭代所得到的A 和H 的估计值。

类似地，式（6）的最小二乘拟合为

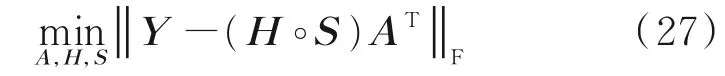
由式（27）可以得到A 的估计为

式中Ĥ和Ŝ为上一次的迭代所得到的H 和S 的估计值。

同理，通过式（7）可以得到Ĥ的估计为

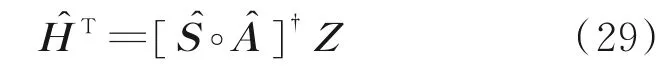
式中Ŝ和Â为上一次迭代所得到的S 和A 的估计值。

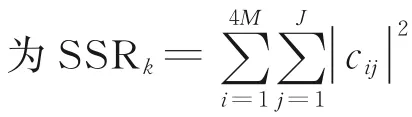
定理［16］考 虑 平 行 因 子 模 型 Xm=HDm(A)ST+Nxm(m=1，2，…，M )， 其 中 ，H ∈C4×K、A∈CM×K、S ∈CJ×K，3 个 矩 阵 的k 秩［15］分别为kH、kA和kS。如果

则S、A 和H 对于列交换和尺度变换是唯一的。

最终可以获得矩阵H 的估计为

式中：Π 为列模糊矩阵，Λ 为尺度因子，W 为估计误差。列模糊问题对角度的估计没有影响，尺度模糊则可以通过归一化方法解决。

对Ĥ进 行 归 一 化 后，设 其 第k 列 为ĥk，定 义rk=ĥk(2)+jĥk(3)，则 可 以 得 到 接 收 信 号 的 仰 角和方位角的估计分别为

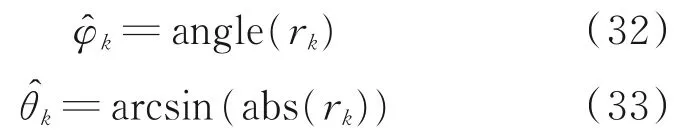
式中：arcsin(·)为反正弦函数，angle(·)表示取元素相角；k=1，2，…，K。上述过程中，由于仰角和方位角从矩阵Ĥ同一列中得到，因此所获得的二维角度已自动配对。此外，由于Ĥ中只包含信号的角度信息，与阵元位置无关，因此本算法能够应用于任意结构的声矢量阵列。

2.3 算法步骤及复杂度、优点分析

上述已经给出了基于快速PARAFAC 分解的二维DOA 估计算法，其主要步骤总结如下：

（1）计算接收信号协方差矩阵，并根据式（14）对协方差矩阵进行分块，然后通过式（17～24）获得矩阵A 和H 的初始估计；

（2）根据式（26，28，29），重复地更新矩阵S、A 和H 的估计值，直到收敛；

（3）根据所获得的H 的估计值，通过式（32，33）得到接收信号的方位角和仰角估计。

对于本文所提算法，参数矩阵初估计过程计算复 杂 度 为O {16M2(J+K )+14K2M +4K3}，单次迭代分解过程复杂度为O {3K3+K2(J+M+4)+6K2(4M+JM+4J )}，因此所提算法总的复杂度为O {16M2(J+K )+14K2M+4K3+n(3K3+K2(J+M+4)+6K2(4M+JM+4J ))}。其 中n为分解迭代次数。图2 和图3 分别为本文所提算法与PARAFAC 算法的收敛速度对比图以及在不同的快拍数下计算复杂度对比图。从图2 和图3中可以看出，所提算法加快了迭代分解过程，计算复杂度大大降低。

图2 迭代分解收敛速度对比Fig.2 Comparision of decompisition convergence rate

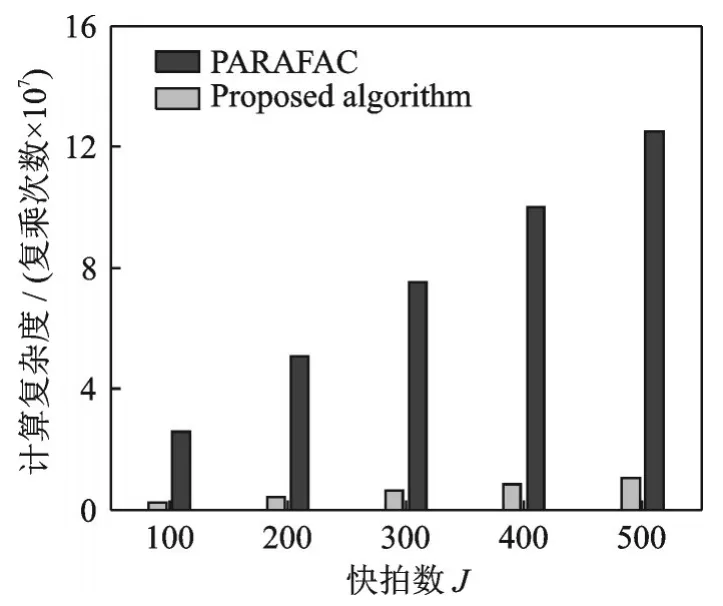
图3 计算复杂度对比Fig.3 Comparision of computational complexity

本文所提算法有如下优点：

（1）本文所提算法能够应用于任意结构的声矢量阵列，同时能得到配对的二维DOA 估计；

（2）本文所提算法借助于矩阵的初估计过程，加快了分解收敛速度，降低了算法的复杂度；

（3）本文算法角度估计性能非常接近于PARA⁃FAC 算法，同时优于ESPRIT 算法和PM 算法。

3 仿真结果

根据前文描述的算法原理及应用场景，本节通过MATLAB 仿真验证本文所提算法的有效性。在仿真中，假设有3 个不相干的远场信源发射的信号，被声矢量传感器阵列所接收，信号波达方向分别 为 (φ1，θ1)=(10°，15°)，(φ2，θ2)=(20°，25°) 和(φ3，θ3)=(30°，35°)。M、J 分别为阵元数和快拍数。仿真中，采用L 次蒙特卡洛仿真来评估算法的角度估计性能，定义角度估计的求根均方误差（Root mean squares error，RMSE）为

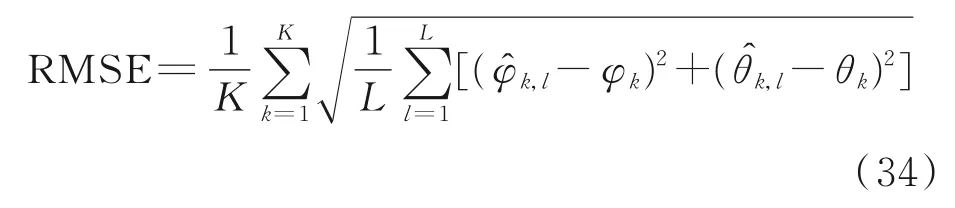
式中：φk、θk分别为第k 个信源的准确方位角和仰角；和分 别 为 第l 次 仿 真 中φk和θk的 估 计值；L 为仿真次数，仿真中L 取1 000。

图4 为本文所提出的算法在信噪比（Signal noise ratio，SNR）为15 dB 下仿真100 次的估计结果分布图。仿真中阵元数M=15、快拍数J=200。从图4 可以看出本算法可以有效地用于声矢量传感器阵列的二维DOA 估计。图5 为本文算法与PARAFAC 算 法［14］、ESPRIT 算 法［8］以 及PM 算法［9］角度估计性能对比仿真结果。仿真中M=10，J=200。从图中可以看出，所提算法角度估计性能非常接近于PARAFAC 算法，同时优于ESPRIT算法和PM 算法。

图6 给出了本文算法在不同阵元数下的仿真结果，仿真中快拍数J=200。从图6 可以看出，该算法性能随着阵元数M 的增大而提高，其原因是阵元数的增多提高了空间分集增益。图7 为本文算法在不同快拍数下的仿真结果，仿真中阵元数M=14。从图7 可知，该算法角度估计误差随着快拍数的增大而减小，其原因为快拍数增大提高了时间分集增益。

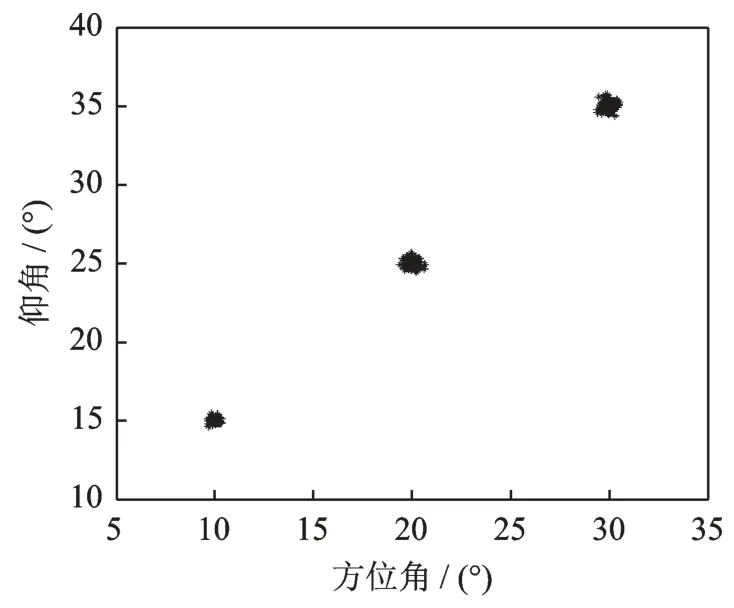
图4 本文所提算法角度估计结果Fig.4 Angle estimation of the proposed algorithm

图5 不同算法的角度估计性能对比Fig.5 Comparison of angle estimation performance of dif⁃ferent algorithms

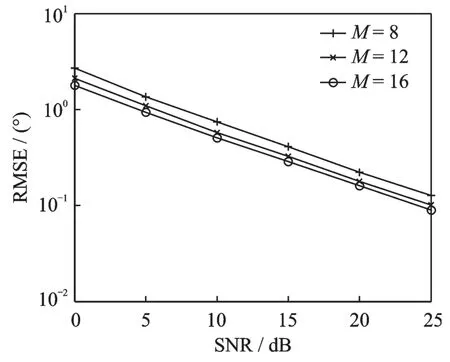
图6 本文算法在不同阵元数下的角度估计性能Fig.6 Angle estimation performance under different M of the proposed algorithm

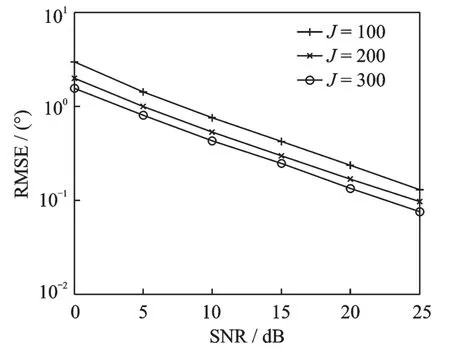
图7 在不同快拍数下的角度估计性能Fig.7 Angle estimation performance under different J of the proposed algorithm

4 结 论

针对任意结构的声矢量传感器阵列中的二维DOA 估计问题，本文提出的快速PARAFAC 分解算法，能够以较低的计算复杂度得到接收信号匹配的二维DOA 估计。仿真表明，该算法的二维角度估计性能接近于PARAFAC 算法，同时优于ES⁃PRIT 算 法 和PM 算 法。