等几何多重网格法在雷诺方程中的应用

李子强 ，罗会信 ，左兵权 ，张 希

（1.武汉科技大学机械自动化学院，冶金装备及其控制教育部重点实验室，湖北 武汉 430081；2.武汉科技大学机械自动化学院，机械传动与制造工程湖北省重点实验室，湖北 武汉 430081）

1 引言

对于雷诺方程的求解，有限差分法[3]和有限体积法[4]对于区域的连续性要求较为严格，结果也容易受到网格插值步长、迭代方法的影响，从而导致求解精度不高；有限元法[2]虽在精度上有提高，但在离散化过程中所花费的时间较长，效率低。等几何法采用CAD 系统中的精确几何模型来执行物理场分析，避免了数值计算的二次建模，节省了求解域的离散过程所花的时间，在工程应用中有较大的优势。这些优势包括精确的几何建模、高阶连续性、简单的网格划分和网格细化等。

等几何法可以在较少的自由度下得到同比于有限元法的求解精度。但随着精度要求的进一步提高，高阶的等几何分析模型依然面临大矩阵，低求解效率的困难。现今大部分的矩阵求解多采用迭代方法计算，多重网格法是普遍采用的方法之一。因此，为了加快高精度要求下等几何法求解雷诺方程效率，将多重网格法与等几何法相结合来对雷诺方程进行求解。

本研究选择雷诺方程作为求解对象，将等几何法，多重网格法与雷诺方程进行适配性研究：首先对雷诺方程进行归一化处理，包括求解域简化为矩形区域，并对雷诺方程进行进一步推导和简化，构建等几何分析模型；结合几何多重网格方法要求，对IGA 法中的细分方法的研究，建立了基于h 细化的多重网格求解模型，提出了基于h细化的多重网格映射矩阵算法；最后引入活塞-缸套润滑系统和滑动轴承两个数值算例，选择W循环和V循环两种循环方式，用高斯-塞德尔迭代法进行求解，并与简单IGA法计算效率进行比较。

2 求解雷诺方程的等几何法

2.1 B 样条与 NURBS 基函数

与有限元法类似，等几何法里面也有“形函数”，即为样条几何自带的NURBS 基函数。但等几何法与有限元法也有明显区别，NURBS 包括节点矢量、控制点向量和权重等要素，而有限元里面只有节点。有限元法是在节点上进行数值计算，等几何法是在控制点上进行数值计算，等几何法与有限元法的基函数的形式也有很大差别。这里首先对样条基函数进行简要介绍。首先给出节点向量：

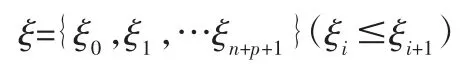
式中：p—基函数的阶数；n—基函数和控制点的个数。B样条基函数可根据节点矢量定义为[6]：

与权重结合得到非均匀有理B样条（NURBS），使用B样条基函数Ni，p（ξ）、Ni，p（η）和权重wi，j可以获得二维 NURBS 基函数其表达式为：

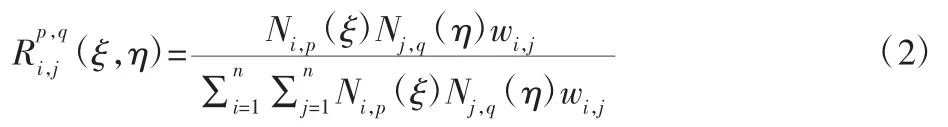
2.2 弱形式的雷诺方程

基于Navier-Stokes 方程和质量连续性方程，可以在做出一些假设后建立雷诺方程[7，8]如下：

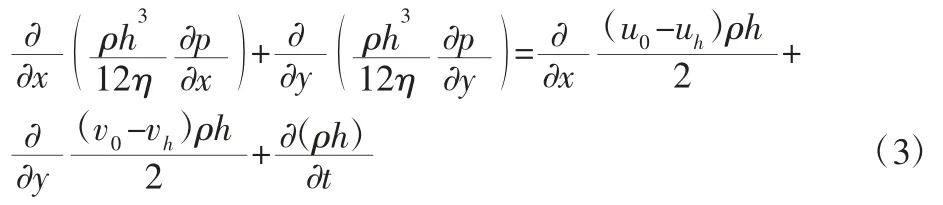
对方程（3）进行变量替换和归一化后，在域D=［0，1］×［0，1］上运用伽辽金法并进行推导获得雷诺方程的弱形式：

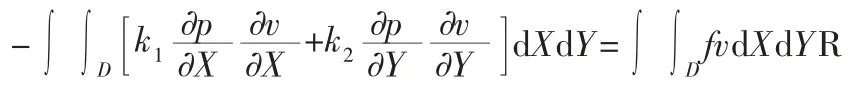
2.3 刚度矩阵推导

在获得雷诺方程的弱形式之后，对雷诺方程的刚度矩阵进行推导。令C=diag（k1，k2），有：

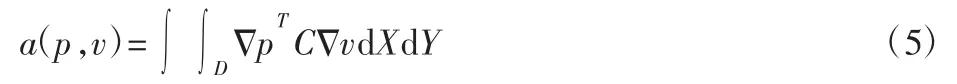
假设物理域D由几何域映射过IGA中NURBS 函数定义为：

对于在参数域D0=［0，1］2上的双变量 NURBS 基函数Rij，以及cij∈R2上的控制点，物理域D上的被积函数g（X，Y）的积分可以转换为参数域上的积分，其积分形式为：

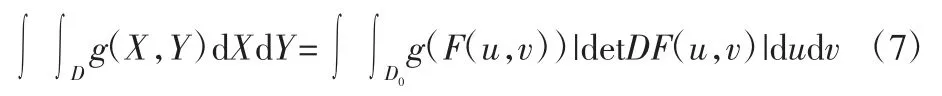
这里，DF是 2×2 雅可比矩阵，基于P（X，Y）=P（F（u，v））的链式规则，微分可以写为：

应用上述变换规则，式（4）左右两端可以分别转化为：

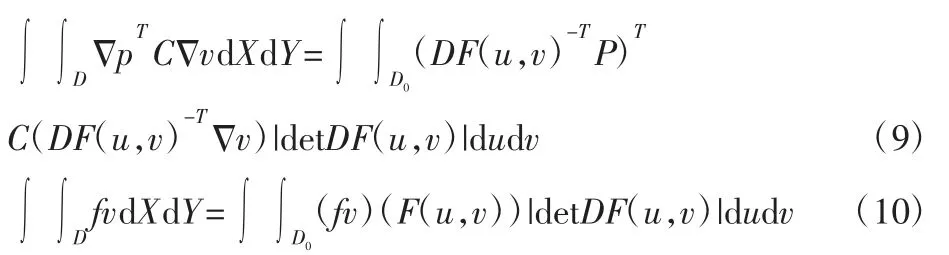
数值解P可以通过NURBS 基函数以及控制点qij∈R近似表示成如下形式：

通过将式（11）代入式（9）中，并用v=Rlk将v进行替换，对于L=1，…，m；K=1，…，n有：

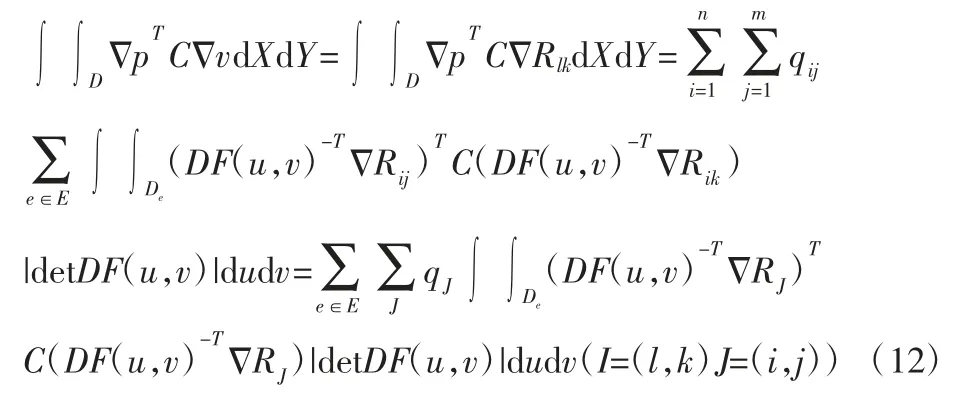
其中，De是参数域的单元，并且获得线性方程组Aq=b，其中这里，单元刚度矩阵Ae=（a（RI，RJ））表示为：

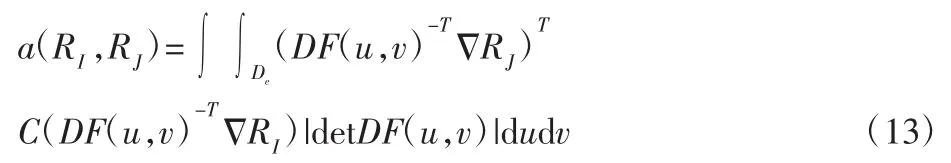
对于I，J=1，…，mn右侧向量b=（＜f，RI＞）的组成部分为：

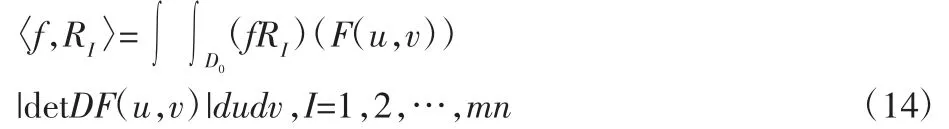
在前文描述的雷诺方程式中，物理域D已被归一化为［0，1］×［0，1］。所以几何域映射定义为F这里的参数域D0=［0，1］2，矩阵DF（u，v）为雅可比矩阵。对式（15）进行适当的推导后，刚度矩阵A可以计算如下：

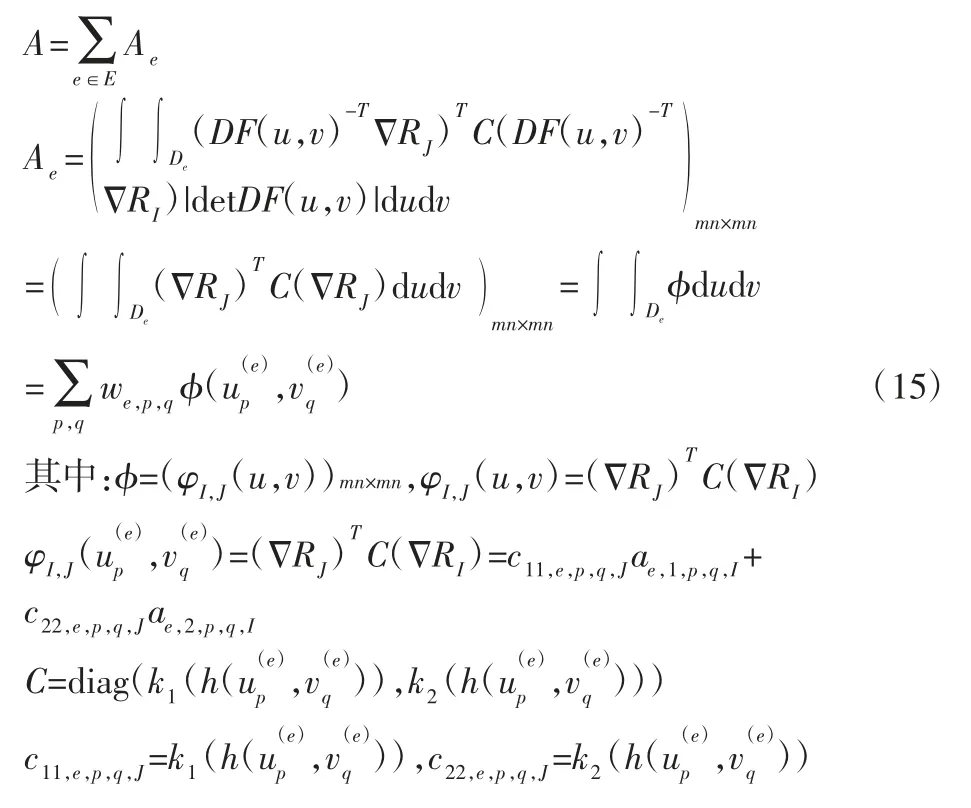
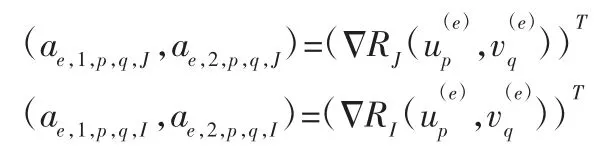
将刚度矩阵进行组装，定义：

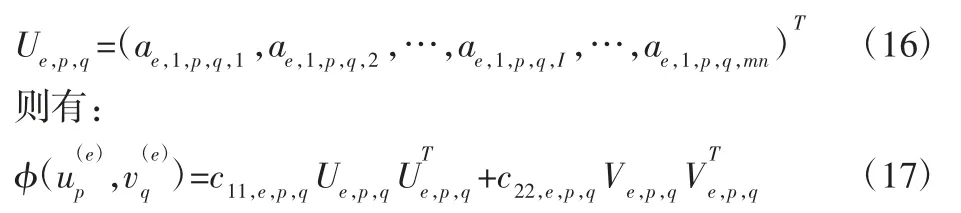
推导出的刚度矩阵为：

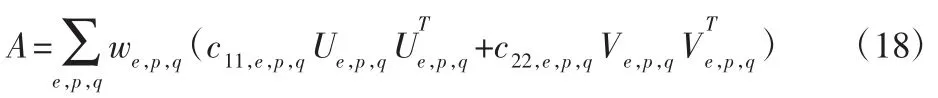
式（18）中we，p，q的是单元De上的高斯积分点处的权重，式（17）中的Ue，p，q和Ve，p，q依赖于 NURBS 基函数和对应的高斯积分点，c11，e，p，q和c22，e，p，q是从高斯积分点处根据油膜厚度 h计算的系数。

3 适于等几何的多重网格法

3.1 多重网格法基本流程和方法

3.1.1 多重网格法的基本思想

上文的推导知，与有限元法类似，等几何法离散之后会得到形如线性方程组Au=f的求解形式，只是刚度矩阵A和右边项f的计算方法不同。求解线性方程组的方法主要有两类一类是直接法，另一类是迭代法，对于雷诺方程来说，虽然等几何法能以比有限元法更少的自由度来表达油膜压力，但有时候为了达到更高的求解精度，自由度数也会比较多，求解的刚度矩阵也会随之变大，当刚度矩阵A比较小且矩阵里面非零元素比较少时，适合用直接法进行求解。对于刚度矩阵维度很大的线性方程组，直接法的求解效率就会很低，这种条件下就需要用迭代法进行求解。在实际的工程问题偏微分方程求解中，大部分都采用迭代法进行求解。其求解公式如下：

收敛速度是数值计算方法的一个重要因素，等几何法也不例外。为了满足更高的精度要求，需要较多的自由度来表达油膜压力，但这样需要更多的迭代法收敛比较慢。为了加快收敛速度，在IGA 求解雷诺方程过程中引入多重网格法。迭代过程中产生的误差分为高频误差和低频误差，当网格密度确定后，高频误差会在迭代过程中快速降低，而低频误差的消除较慢。而在网格密度变粗以后，细网格的低频误差在粗网格里面频率就显得相对较高，所以粗网格误差收敛速度相对更快。多重网格法再细网格上满足精度要求，用粗网格实现快速收敛。

3.1.2 多重网格法的基本流程

重网格法通过构建不同网格之间的映射关系进而加速计算，其中包含由粗到细的延拓矩阵R和细到粗的限制矩阵P。依据粗网格刚度矩阵的来源不同分为两类，一类是几何多重网格法，一类是代数多重网格法，它们的求解流程是基本相同。其中代数多重网格法对映射矩阵给出了如下限制：

而几何多重网格则是基于网格层次关系的不同而构建出来的。这里采用的是几何多重网格法，其求解方法将在下文进行详细说明。多重网格法的基本思路是利用粗网格消除细网格上的低频误差，以达到更快收敛的目的。这里以V循环为例对多重网格法基本流程进行表述：

该方法用三层控制点网格对雷诺方程进行求解，第一层较细网格上的求解结果作为最终计算结果，用第二层较粗控制点网格对第一层细网格的求解进行加速，用第三层最粗网格对第二层网格上的计算进行进一步的加速。W循环类似。

从上面可以看出，求解过程需要两个映射关系，一个是将rh从Ωh映射到Ω2h得到r2h的映射关系（即限制矩阵P），另一个是将e2h从Ω2h映射到Ωh上得到eh的映射关系（延拓矩阵R）。这是多重网格方法计算的关键，能否得到这个映射关系直接决定了方法的可行性。

3.2 多重网格的生成

基于有限元的多重网格法的映射关系局限在单元内，细网格上节点的待解物理量可由粗网格上相应单元上的相关节点线性地表达，粗网格上要求解的节点的物理量也是由细网格上相应单元节点线性表示。而等几何分析方法中的基函数对应的作用范围是跨单元的，所以对应的多重网格间的映射关系也需要是跨单元的。由于等几何是在控制点上进行数值计算，所以网格上对应的网格点是NURBS 里面的控制点。控制点的坐标由节点的坐标进行表达，所以每一次细化都是先在原来的节点向量上插入一些节点形成新的节点向量，然后再根据新的节点向量和原来的控制点和节点向量的值计算得到新的控制点。等几何法中网格细化方法有h细化、p细化和k细化，由于经p细化和k细化都需要对基函数进行升阶，而传统多重网格法中不同网格上没有阶次的差别，因此文中选用基于h细化的方式对网格进行细化，故有必要分析一下等几何分析方法中的h细分算法。这里先以一维为例，介绍一下h细分方法。设已给一条k次B样条曲线：

其中，B 样条基函数只由节点向量 τ=［τ0，τ1，…，τn，τn+k+1］中的节点进行表达。如果在定义域内某个节点区间内插入一个节点t∈［τi，τi+1］⊂［τk，τn+1］以得到新的节点矢量T=［τ0，τ1，…，τi，t，τi+1，…，τn，τn+k+1］重新编号后成为T=［t0，t1，…，ti，ti+1，ti+2，…，tn+k+2］。然后根据新的节点矢量表达一组新的B样条基函数0，1，…，n+1）。然后原样条曲线可以用新的B样条基函数与未知新顶点Di（j=0，1，…，n+1）共同表示为：

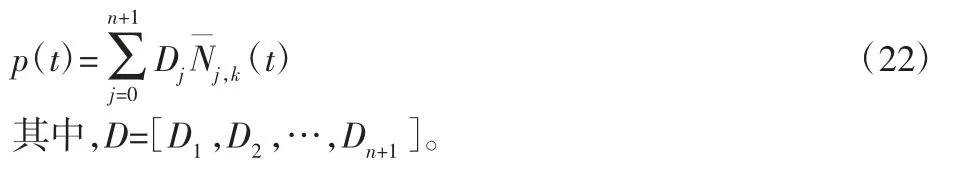
具体细分算法参考文献[10]。

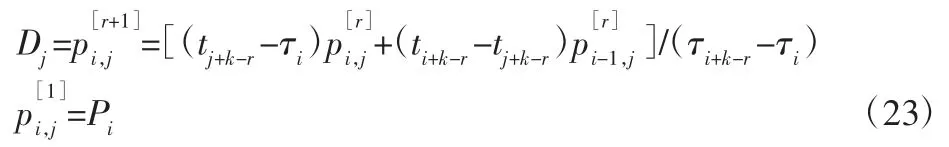
式中：Di—细网格控制点；Pi—粗网格控制点；i—粗节点向量上ti所在位置左边的节点编号；k—基函数阶数；t—细节点向量上节点值；τ—粗节点向量上节点值，r的值从k-1 开始随着公式的递推减1，直至r=1。

由于选择的NURBS 基函数是三阶的，故k=3，按上述公式可得，如式（24）所示。

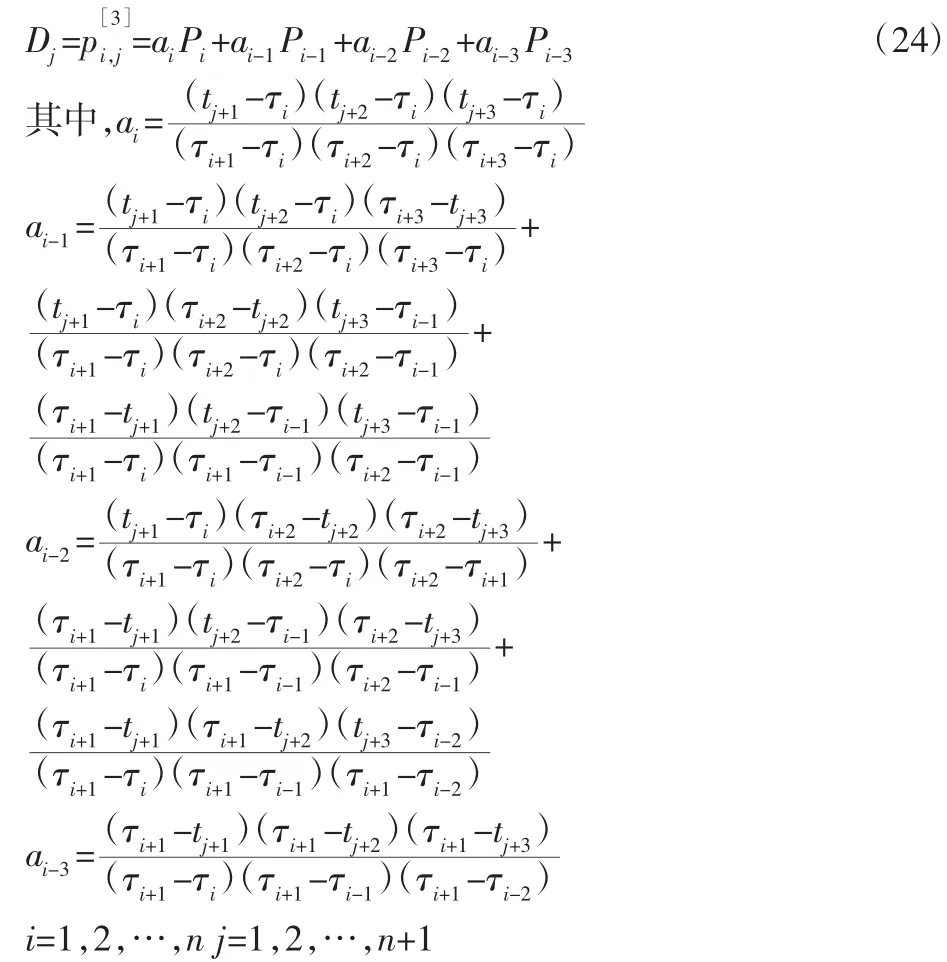
这样即可得到新的控制点向量D=［D1，D2，…，Dn+1］。

由于计算对象的求解域是二维的，所以在进行网格细化时分别要在两个方向插入节点来进行网格细化（三维方向同理）。若需要l层网格，在最初网格上进行l-1 次网格细化即可。

对于二维求解域，依次对两个维度节点向量分别插入节点，得到的细化算法如下：

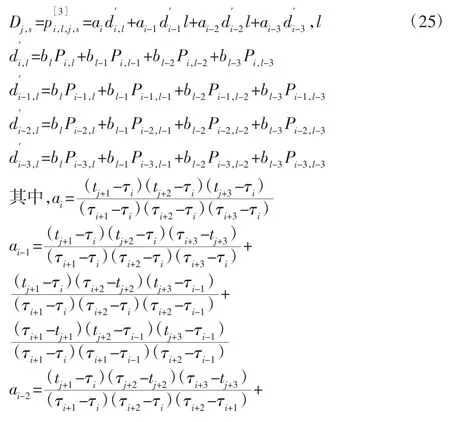
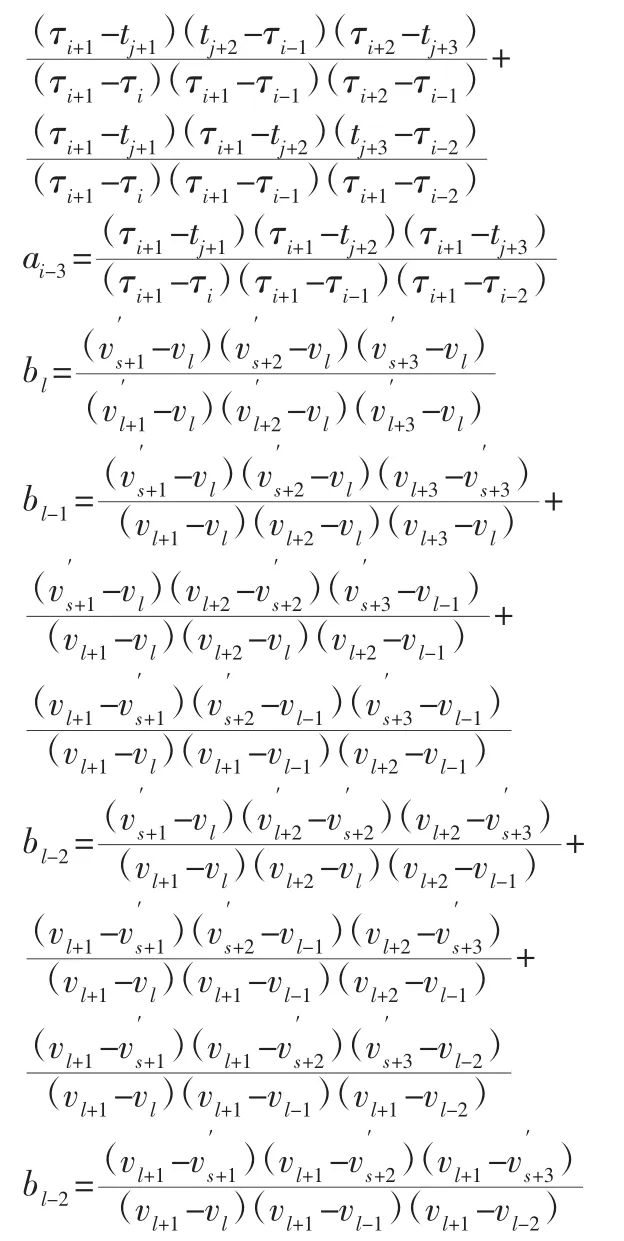
式中：V，V′—第二方向上的粗、细节点向量。

然后用式（25）计算方法对网格进行细化，一粗网格控制点网格和经过一次细化后的细控制点网格图，如图1 所示。

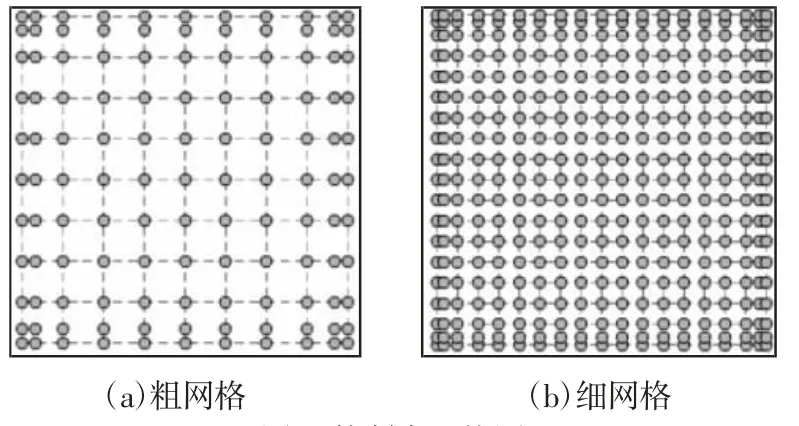
图1 控制点网格图Fig.1 Control Point Grid Diagram

等几何的控制点都是由求解域内初始控制点进行细化得到。这种方法使多重网格的生成更加简单，需要三层控制点网格，当进行l次细化时，保存第l-2 次细化得到的控制点作为第三层，这一层控制点网格最粗，然后在进行两次细化，分别得到的二层相对较粗的控制点网格和第一层最细控制点网格。得到三层控制点网格后，根据等几何法求出各层网格上的刚度矩阵A1，A2，A3和最细网格上的右边项f1。

3.3 多重网格法映射矩阵

与节点的细化方式对应，映射矩阵也是按照文献[10]中的方法进行求解。根据式（23）推导出的式（24）的计算方法，当插入一个节点时，新的控制点向量和原控制点向量就会出现一个对应的映射关系R，此时新的控制点有n+1 个，而原控制点有n个。则新控制点向量和原控制点向量基于R的映射关系为：

以一个一维三次B样条为例，其原有节点向量为τ=［0 0 0 0 1 1 1 1］，原有控制点向量为P=［0 0.333 0.6667 1.0000］。

当在原始节点向量中插入一个节点t=0.5，就会得到一个新的节点向量t=［0 0 0 0 0.5 1 1 1 1］，和一个新的控制点向量D＝［D1D2D3D4D5］，按照式（24）即可得到如下映射关系：D=D5×4P，此时的映射矩阵为：

而在h细化中，往往要插入的节点数目不只一个。在这种情况下，可依次单独插入相应的节点来得到新的节点向量和控制点。例如要在节点向量 τ=［τ0，τ1，…，τn，τn+k+1］，中插入节点t1，t2，…，tm，此时依然可以按照式（24）得到新的控制点：

其中R（n+m）Xn即为粗网格到细网格的映射矩阵。

这里雷诺方程的求解域是二维的。其粗细网格间的映射矩阵可根据式（25）计算得到。

对细网格上每个控制点根据式（27）建立线性映射关系，即可组装得到粗网格到细网格之间的整体映射矩阵R。由于细网格到粗网格的映射矩阵（即限制矩阵P）的求解比较困难，这里采用文献ade 的方法求该映射矩阵，即映射矩阵P取R的转置。

由式（24）可以发现，对于一维求解域，一个细网格控制点由4 个粗网格控制点线性表达，由式（25）可以看出，对于二维求解域，一个细网格控制点由16 个粗网格控制点线性表达，其映射关系，如图2 所示。细网格向粗网格映射时，粗网格上的每个控制点也是由同样数目的细网格控制点线性表达。粗、细网格上的映射关系是跨单元的，这样就得到两层控制点之间更好的线性关系。这种跨单元多对一的映射关系，有利于提高计算的稳定性。

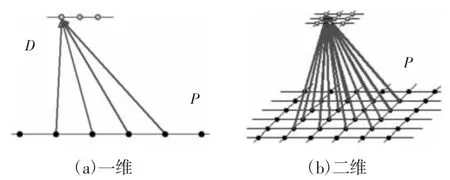
图2 粗细网格控制点映射关系示意图Fig.2 Schematic Diagram of Point Reflecting Relationship between Coarse and Fine Grid Control Points

4 数值算例

4.1 模型的数值求解

这里先分别用有限元法和等几何法对活塞-缸套润滑模型进行求解，通过各种自由度下两种数值算法的油膜压力积分值的对比来比较两种解法的效果；然后分别用等几何法和多重网格法多活塞-缸套和径向滑动轴承两种模型进行求解，并以全主元高斯消去法得到的值作为标准值，将得到的值与标准值相对误差以10 为底求对数作为误差参数e，求解与迭代次数对应的误差值，绘制e-迭代次数折线图。误差参数e的表示方法，如式（28）所示。

其中，U=Ah＼fh，u是等几何法、迭代法等得到的近似解。

4.2 内燃机活塞-缸套润滑模型

通过对活塞缸之间的膜润滑的雷诺方程进行求解得到的油膜压力。活塞-缸套系统，如图3（a）所示。其油膜润滑区域[9]，如图3（b）所示。

图3 活塞--缸套润滑系统示意图Fig.3 Piston-Cylinder Liner Lubrication System

因为左右润滑区域相对于平面φ=0 都是对称的，所以只需考虑前面部分。通常，当活塞周期性地移动时，由于负载变化，密度和粘度的大小会发生变化。但为了简化数值模型，这里将密度和粘度的值作为常数。给定油膜压力的参数，如表1 所示。

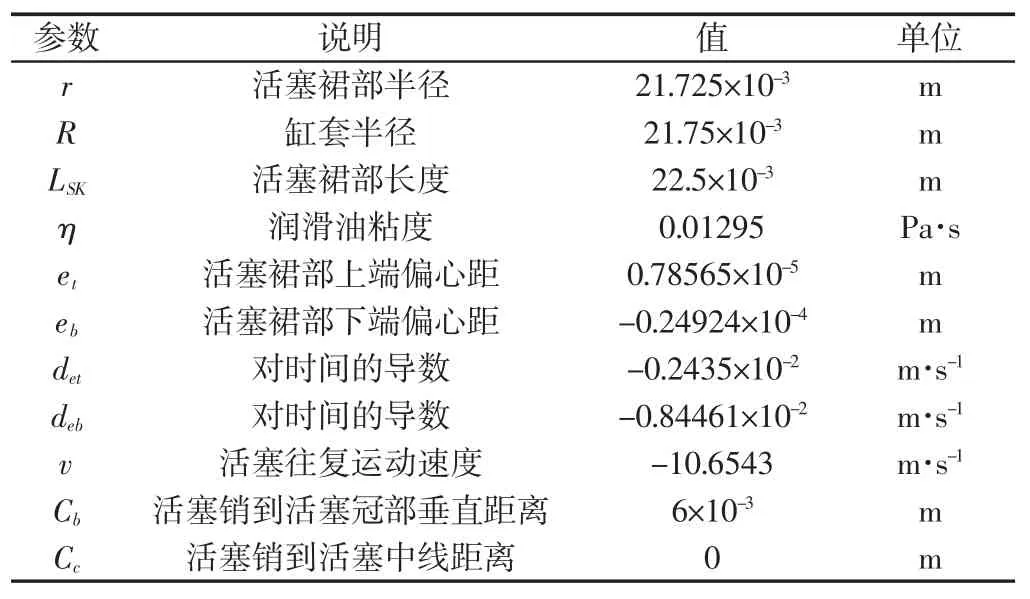
表1 计算参数Tab.1 Calculate Parameters

假设v0=0，vh=v（其正方向为上行），润滑剂无侧漏，因此u0=uh=0。那么有：

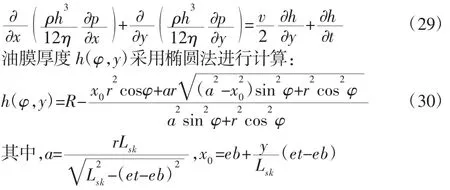
将求解域D归一化为［0，1］×［0，1］，进行如下转换：

右侧（因为对称，只考虑前面部分）

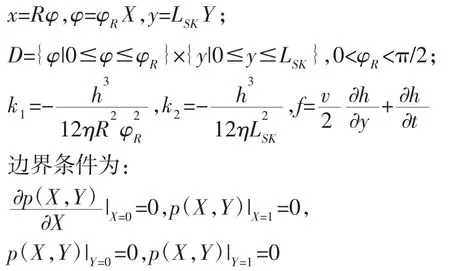
（1）等几何法与有限元法精度比较

分别用有限元法和等几何法对活塞-缸套润滑模型油膜压力进行求解，并将其比较两种算法得到的压力积分随自由度变化的趋势。其结果，如图4 所示。

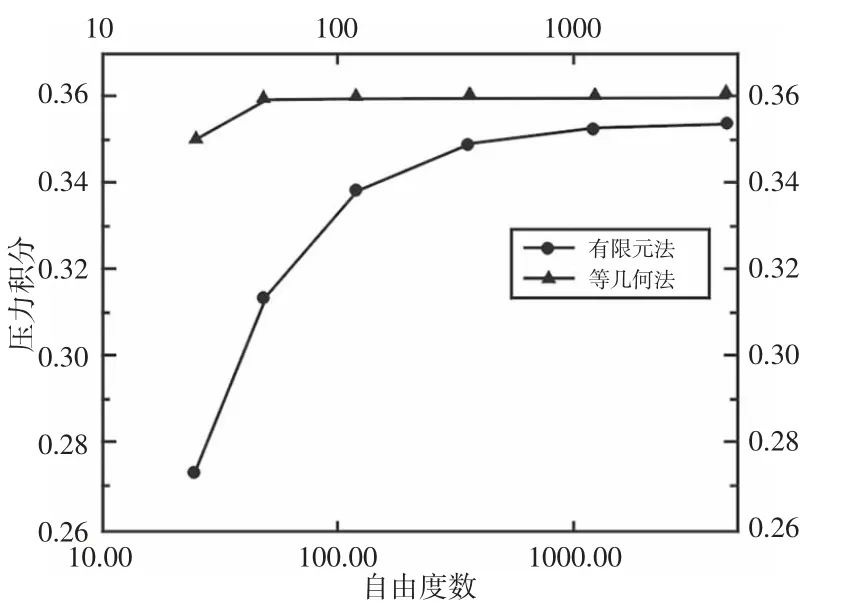
图4 不同自由度时有限元法和等几何法压力积分图Fig.4 Pressure Integral of FEM and Isogeometric Under Different Degree of Freedom

根据图4 可以看出，随着自由度的增加，两种数值算法都更趋近于收敛值，但等几何法趋近的速度更快。因此可以证明在自由度相等的情况下，等几何法的精度高于有限元法。这种特性综合了有限差分法和有限元法的速度与精度的优势，非常适合流体仿真分析。

（2）将雅可比迭代、高斯塞德尔迭代、超松弛迭代三种代法与等几何多重网格法的求解效率一起进行对比。超松弛迭代松弛因子的值根据最佳松弛因子选取。求解得到的油膜压力图和r-迭代次数趋势图，如图5、图6 所示。

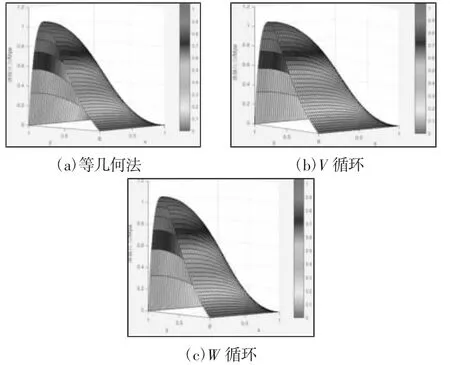
图5 缸套活塞油膜压力Fig.5 Oil Film Pressure of Cylinder Piston

图6 缸套活塞e-迭代次数图Fig.6 e-Iteration Number Diagram For Cylinder Liner Piston

从图6 可以看出，在迭代次数从25 增加到400 的过程中，高斯塞德尔迭代和雅可比迭代收敛速度都最慢，SOR 的收敛效率相对较快，多重网格法收敛速度最快。在迭代次数为25 时，SOR、高斯塞德尔迭代和雅可比迭代的误差相差不大，多重网格法误差相对较小，在迭代次数为400 时，高斯塞德尔迭代和雅可比迭代的误差接近e-2，SOR 迭代误差在e-6 到e-7 之间，而多重网格法迭代误差接近e-10。因此用高斯塞德尔迭代和雅可比迭代时，单纯等几何法收敛速度很慢，在改用SOR 进行迭代后，速度明显加快，但仍然明显比等几何多重网格法收敛速度慢。多重网格法在迭代过程中收敛速度曲线出现了拐点，在拐点后比拐点前的趋势更加平缓，此处是由于限制矩阵P是通过取延拓矩阵R的转置得到的，而不是进行理论计算得到。这样会使限制矩阵的映射有一定偏差，由于刚开始迭代时得到的数值解与真实值的误差较大，这种偏差的影响较小，但当误差较小时，这种偏差的影响就显得很明显。

4.3 径向滑动轴承模型

在稳态条件下的径向滑动轴承的润滑模型，如图7 所示。

图7 径向滑动轴承润滑模型Fig.7 Radial Plain Bearing Lubrication Model

径向滑动轴承油膜压力的计算参数，如表2 所示。

表2 计算参数Tab.2 Calculate Parameters

层流状态下不可压缩流体动压的二维润滑雷诺方程为[10]：

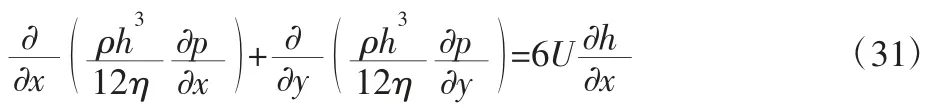
将求解域D归一化，得到雷诺方程的系数项和右边项x=

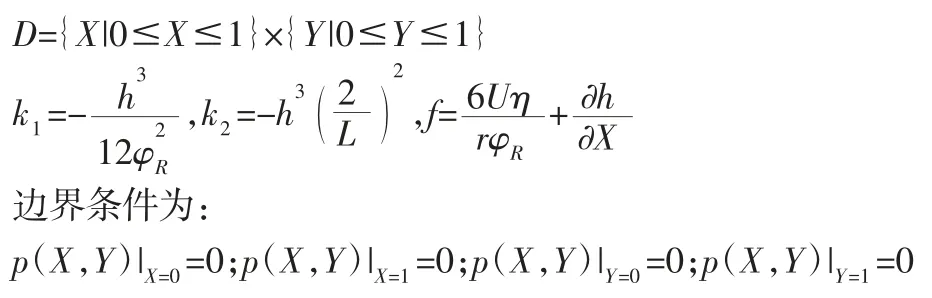
光滑滑动轴承的油膜厚度公式为：

将雅可比迭代、高斯塞德尔迭代、超松弛迭代三种代法与等几何多重网格法的求解效率一起进行对比。超松弛迭代松弛因子的值依据最佳松弛因子选取。求解得到的油膜压力图和r-迭代次数趋势图，如图8、图9 所示。

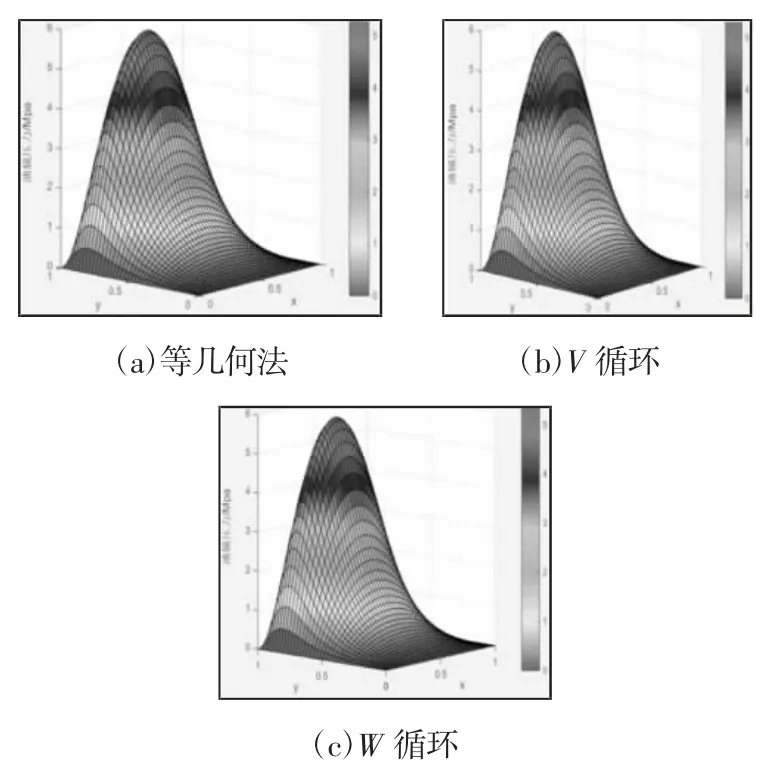
图8 径向滑动轴承油膜压力Fig.8 Oil Film Pressure of Radial Sliding Bearing

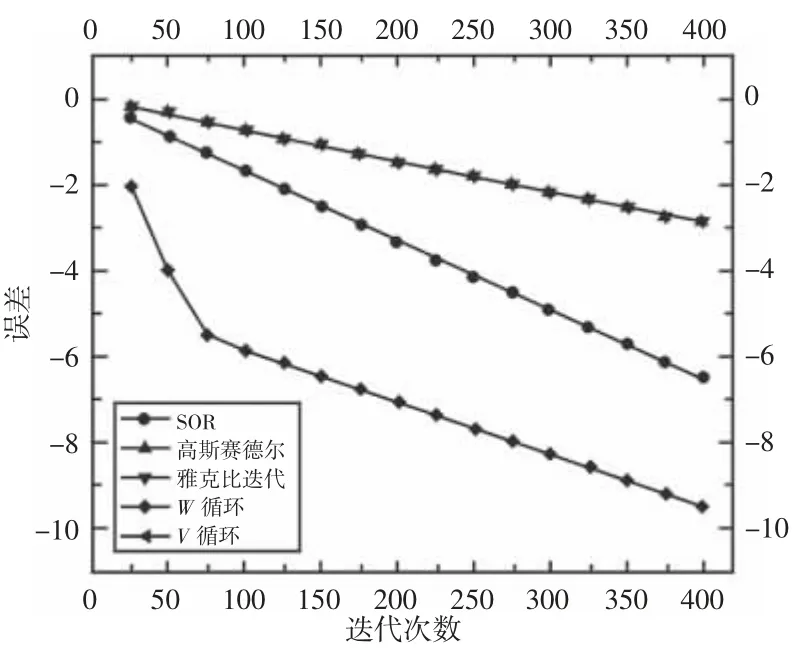
图9 径向滑动轴承e-迭代次数图Fig.9 e-Iteration Number Diagram of Radial Sliding Bearing

从图9 可以看出可以得到与缸套活塞润滑模型相似的结论。不同的是两种模型里面高斯塞德尔迭代和雅可比迭代的收敛速度有较小差别，而且两种模型的多重网格法迭代收敛曲线拐点出现的位置不同。这两种区别的形成是由于两种模型不同参数形成了不同的刚度矩阵的特征。

5 结论

在二次精度NURBS 样条的基础上，对雷诺方程进行推导，并对节点插入的细分算法进行研究，提出基于h细化的细分算法，并建立适于等几何多重网格法的求解模型，提出基于h细化的映射矩阵求解方法。引入缸套活塞润滑系统和径向滑动轴承两个数值算例，先用单纯等几何法和有限元法对活塞-缸套润滑模型进行求解，比较不同自由度条件下的压力积分。计算结果证明等几何法的求解精度明显高于有限元法。在此基础之上，分别通过基于单纯等几何法的雅可比、高斯塞德尔和超松弛迭代三种代法和等几何多重网格法对活塞-缸套润滑模型和径向滑动轴承润滑模型油膜压力进行求解，比较其收敛速度。

根据计算结果可以得出如下结论，相比于有限元法，等几何法求解雷诺方程能以较小的自由度实现更高的精度。超松弛迭代的收敛效率高于雅克比迭代和高斯塞德尔迭代，但引入多重网格法进行求解后，收敛效率明显高于超松弛迭代、雅克比迭代和高斯塞德尔迭代；由于限制矩阵P是通过取延拓矩阵R的转置的方法得到而造成映射偏差，造成多重网格法收敛曲线出现拐点；对于相同的迭代方法，两种模型的收敛趋势有较小的区别，是由于不同模型刚度矩阵的特征不同。